
TVSP_2
.pdf
Случайная величина называется нормальной или гауссовской, если ее плотность распределения вероятностей имеет вид
|
1 |
|
− |
(x−a)2 |
|
Wнорм( x ) = |
|
2σ2 |
(4.8) |
||
2π |
σ |
e |
, |
||
|
|
|
|
где a и σ (σ>0) – параметры распределения. Функция распределения вероятностей нормально распределённой случайной величины не выражается в элементарных функциях. Ее значения для стандартной случайной величины, имеющей параметры a = 0 и σ = 1, приведены в таблице в прил. 1.
Учитывая, что плотность вероятности нормального рас-
пределения является |
четной |
функцией |
относительно точки |
||||||||
x = a, для вероятности попадания СВ ξ |
в интервал значений, |
||||||||||
симметричный по отношению к этой точке |
(с учетом свойств |
||||||||||
из прил. 1), получаем |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
a+ |
(x-a)2 |
|
1 |
/σ |
|
z2 |
|||
P{ a– ≤ ξ ≤ a+ } = |
∫ e- |
|
dx = |
∫ |
e- |
|
dz = |
||||
2σ 2 |
|||||||||||
2 |
|||||||||||
|
2π σ a− |
|
|
|
2π |
− /σ |
|
|
|
||
= Fст( /σ ) – Fст( – |
/σ ) = 2·Fст( |
/σ ) – 1. |
(4.9) |
||||||||
18
5. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Начальным моментом k-го порядка случайной величины ξ называется константа, к которой стремится среднее арифметическое k-тых степеней значений, принятых величиной ξ в бесконечно большой серии опытов. Для дискретной случай-
ной величины (ДСВ), принимающей значения |
xi с вероятно- |
стями pi, этот начальный момент определяется формулой |
|
mk{ ξ } = ∑ xik pi , |
(5.1) |
i |
|
где в суммировании участвуют все возможные значения СВ ξ. Для непрерывной случайной величины (НСВ), характеризуемой плотностью вероятности Wξ(x), начальный момент k-го порядка рассчитывают по формуле
+∞ |
|
mk{ ξ } = ∫xk Wξ (x) dx . |
(5.2) |
-∞
Особое место среди начальных моментов занимает начальный момент первого порядка, называемый математическим ожиданием. Математическое ожидание случайной величины ξ определяет константу, к которой стремится среднее арифметическое наблюдаемых значений этой СВ, и может быть рассчитано по правилу
|
∑ xi pi |
- для ДСВ, |
|
i |
|
|
(5.3) |
|
Mξ = m1{ ξ } = |
+∞ |
|
|
∫x Wξ (x) dx |
- для НСВ. |
|
-∞ |
|
Примечание: Геометрически математическое ожидание соответствует горизонтальной координате центра масс фигуры, образуемой плотностью вероятностей анализируемой случайной величины.
19
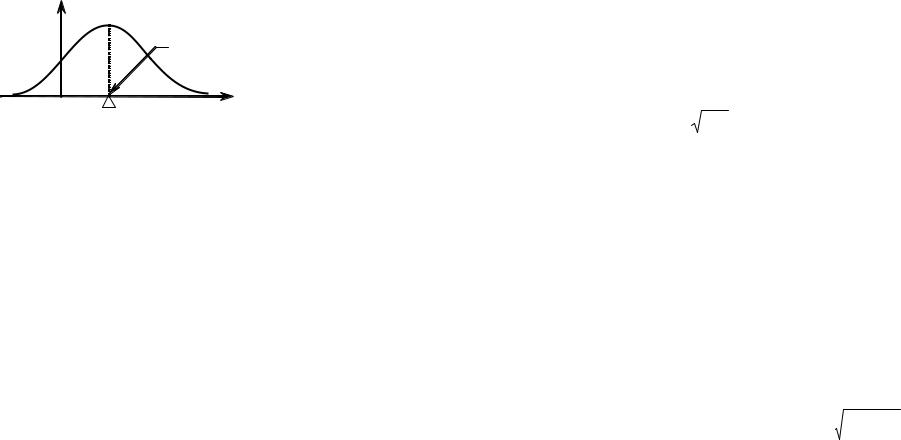
Это означает, что если под графиком ПРВ разместить в точке x = Mξ опору, то на данной опоре фигура, образуемая графиком ПРВ, будет находиться в равновесии. Из этого, в частности, следует, что для любой СВ, плотность вероятности которой оказывается четной относительно некоторой точки, эта точка и определяет математическое ожидание (рис. 3).
Wξ(x)
Mξ
0 |
a |
x |
Рис. 3. Для СВ с симметричной плотностью вероятности математическое ожидание находится в центре симметрии
Центральный момент k-го порядка определяется аналогично (5.1)-(5.2), но отличается от начального тем, что усреднению подвергаются k-е степени отклонений наблюдаемых значений СВ ξ от ее математического ожидания. Соответственно, расчетная формула для k-го центрального момента имеет вид
|
∑ (xi − Mξ )k pi |
- для ДСВ, |
|
i |
|
|
(5.4) |
|
μk{ ξ } = |
+∞ |
|
|
∫(x − Mξ )k Wξ (x) dx |
- для НСВ. |
|
-∞ |
|
Важнейшим центральным моментом случайной величины является её второй центральный момент, называемый дисперсией. Дисперсия Dξ характеризует степень разброса значений, принимаемых случайной величиной, относительно ее математического ожидания. Она рассчитывается по правилу
20
|
∑(xi − Mξ )2 pi |
- для ДСВ, |
|
|
|||
Dξ = μ2{ ξ } = |
i |
(5.5) |
|
|
+∞ |
|
|
∫(x − Mξ )2 Wξ (x) dx |
- для НСВ. |
||
|
|||
−∞ |
|
||
Из (5.5) несложно также получить следующее, полезное во многих практических ситуациях, соотношение
Dξ = m2{ ξ } – Mξ2. |
(5.6) |
Часто вместо дисперсии в расчетах используют средне-
квадратическое отклонение (СКО) или, иначе, эффективное
значение случайной величины |
|
σξ = Dξ . |
(5.7) |
Эффективное значение, как и дисперсия, характеризует степень разброса значений, принимаемых случайной величиной, и отличается от нее единицей измерения.
|
|
|
Таблица 5.1 |
|
Свойства числовых характеристик случайной величины |
||||
|
|
|
|
|
Свойство |
Матожида- |
Дисперсия |
СКО |
|
ние Mη |
Dη |
ση |
||
|
||||
Размерность |
[ η ] |
[ η ]2 |
[ η ] |
|
Для константы η = c |
c |
0 |
0 |
|
|
|
|
|
|
После умножения на |
c · Mξ |
c2 · Dξ |
|c| · σξ |
|
константу η = c · ξ |
||||
|
|
|
||
|
|
|
|
|
Для линейного преоб- |
|
|
|
|
разования η = ∑ai ξi |
∑ai Mi |
∑ai2 Di |
∑ai2 Di |
|
i |
i |
i |
i |
|
некоррелированных ξi |
|
|
|
|
Примечание: обозначение [ η ] соответствует размерности случайной величины η.
21

6. ФУНКЦИОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
Если каждое значение y случайной величины η возникает как реакция на соответствующее значение x воздействия ξ : y = f( x ), то говорят, что случайные величины ξ и η связаны функциональной зависимостью η = f( ξ ). Следствием зависимости между наблюдаемыми значениями СВ является жесткая взаимосвязь между их законами распределения.
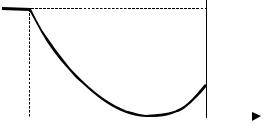
Пусть ξ является непрерывной СВ, а функция y = f( x ) не содержит горизонтальных участков (пример подобной функции показан на рис. 4). Тогда каждое выходное значение y может быть получено из конечного числа аргументов x, т.е. существует конечнозначная обратная функция x = φi(y), где i – номер ветви обратной функции φ(·). В частности, для случая, представленного на рис. 4, обратная функция является одно-
значной для y ( –∞; y0 ] |
и трехзначной – для y [ y0; y1 ] (три |
||||
разных значения |
x* = φ1(y*), x* = φ2(y*) и x* = φ3(y*) соответст- |
||||
|
|
1 |
2 |
3 |
|
|
y = f( x ) |
|
вуют одному и тому же y* ). |
||
|
|
|
|||
y1 |
|
|
|
Рис. 4. Пример функци- |
|
|
y* |
|
|
||
|
|
|
ональной зависи- |
||
|
|
|
|
||
y0 |
|
|
|
мости с конечно- |
|
x* 0 |
x* |
x0 x* |
x, В |
значной обратной |
|
функцией |
|||||
1 |
2 |
3 |
|
||
|
|
||||
Если для каждого возможного значения выходной СВ η обратная функция оказывается конечнозначной, то закон распределения η определяется соотношением
Wη( y ) = ∑ Wξ(ϕi ( y)) |
dϕi ( y) |
, |
(6.1) |
|
dy |
||||
i |
|
|
где суммирование идет по всем ветвям обратной функции.
22
Если функция y = f(x), преобразующая непрерывную СВ ξ в СВ η, напротив, состоит лишь из горизонтальных участков (как показано на рис. 5), то получаемая СВ η оказывается дискретной, т.к. возможными (наблюдаемыми) для нее будут лишь отдельные значения ym (на рис. 5 подобных значений четыре – от y1 до y4 ).
|
|
|
|
y = f( x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
y4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
y3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
y1 |
x4 |
x, В |
||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 5. Пример преобразования непрерывной СВ в дискретную
Провести в этом случае расчет по формуле (6.1) уже невозможно, т.к. каждому из значений ym соответствует бесконечно много аргументов x. Так, значению y1 соответствуют любые аргументы x, удовлетворяющие неравенству x < x1; значению y2 – любые аргументы, принадлежащие интервалу x [ x1; 0 ], и т.д. В результате оказывается неопределенным (бесконечным) число ветвей, которые нужно суммировать в (6.1).
Учтем, однако, что возникающая в результате преобразования СВ η является дискретной. Закон распределения подобной величины определяется лишь вероятностями, с которыми наблюдаются ее отдельные значения ym. Вместе с тем СВ η принимает значение ym в тех и только тех случаях, когда значение исходной СВ ξ лежит в пределах соответствующего этому ym интервала оси x. Так, применительно к рис. 5 вероятность появления значения y1
x1
P{ η = y1 } = P{ ξ ≤ x1 } = ∫ Wξ (x) dx .
−∞
23
Аналогично, для уровня y2 имеем
0
P{ η = y2 } = P{ x1 ≤ ξ < 0 } = ∫ Wξ (x) dx
x1
и т.д. Поскольку записанные выше вероятности приходятся на отдельные точки оси x плотность вероятности в этих точках оказывается бесконечно большой и может быть записана посредством дельта-функции
Wη( y ) = ∑ P{η = ym } δ(y − ym ) , |
(6.2) |
m |
|
где число слагаемых определяется количеством горизонтальных участков зависимости y = f( x ).
Объединяя воедино оба рассмотренные выше случая, по-
лучаем следующую универсальную формулу, определяющую вероятностные свойства результата функционального преобразования случайной величины
Wη(y) = ∑Wξ (ϕi ( y)) |
|
|
dϕi ( y) |
|
|
+ ∑P{η = ym } δ(y − ym ) , (6.3) |
|
dy |
|||||||
i |
|
|
|
|
m |
||
|
|
где первая сумма включает все ветви обратных функций по всем наклонным участкам зависимости y = f( x ), а вторая сумма – все горизонтальные участки той же самой зависимости.
Числовые характеристики функционально преобразованной случайной величины η могут быть рассчитаны по стандартным правилам (на основе найденной Wη(y) ), а могут быть получены, минуя этап нахождения её закона распределения вероятностей:
|
+∞ |
|
|
M η = ∫ f(x) Wξ (x) dx , |
(6.4) |
|
−∞ |
|
+∞ |
+∞ |
|
Dη = ∫[f(x) - Mη]2 Wξ (x) dx = ∫[f(x)]2 Wξ (x) dx − M η2 . |
(6.5) |
|
−∞ |
−∞ |
|
|
24 |
|
Пример. Случайная величина ξ, обладающая плотностью вероятности Wξ(x) = ex при x ≤ 0, подвергается функцио-
нальному преобразованию η = |
16, при ξ ≤- 6 , |
|
(ξ + 2)2 , при иных ξ. |
Определить закон распределения и математическое ожидание СВ η.
Решение Начнем решение задачи с построения и анализа графика
функциональной взаимосвязи |
|
|
y = f(x) = |
16, при x ≤- 6 , |
(6.6) |
|
(x +2)2 , прииных x. |
|
Из графика, представленного на рис. 6, следует, что при x ≤ 0 значения, получаемые в результате преобразования, лежат в диапазоне от 0 до 16, однако различным частям этого диапазона соответствует разное число ветвей в обратной функции.
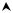 y = f(x) 16,0
y = f(x) 16,0















 4,0
4,0
-6 |
-5 -4 |
-3 |
-2 |
-1 |
0 |
x |
Рис. 6. Функциональная зависимость, анализируемая в примере
25
Значениям y [ 0; 4 ] соответствует по два возможных аргумента x, определяемых ветвями обратной функции x1 =
= φ1(y) = +  y – 2 и x2 = φ2(y) = –
y – 2 и x2 = φ2(y) = –  y – 2. На данном участке
y – 2. На данном участке
слагаемые, входящие в “сумму по m” формулы (6.3) не потребуются, а первая сумма (по ветвям обратной функции) будет содержать два слагаемых
|
|
|
2 |
|
|
|
|
dϕi ( y) |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Wη( y ) = ∑Wξ (ϕi ( y)) |
= |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
i=1 |
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
= |
+ |
|
− |
2)) |
+ |
1 |
+ |
|
− |
|
− |
2)) |
− |
1 |
= |
e−2+ y +e−2− y |
||
y |
2 y |
Wξ |
y |
2 y |
|
. |
||||||||||||
|
Wξ ( |
|
|
|
|
( |
|
|
|
|
2 y |
|||||||
|
Значениям |
y, удовлетворяющим неравенству |
4 < y < 16, |
|||||||||||||||
соответствует единственный аргумент |
x = φ(y) = – |
y –2, по- |
||||||||||||||||
этому вместо указанных ранее двух слагаемых остается лишь одно
Wη( y ) = W |
(ϕ( y)) |
dϕ( y) |
= e−2− y . |
|
|||
ξ |
dy |
2 y |
|
|
|
||
И, наконец, горизонтальному участку y = 16 соответствует бесконечный по протяженности интервал x ≤ –6, вероятность попадания в который для СВ ξ определяется интегралом
P{ η = 16 } = P{ ξ ≤ –6 } = −∫6 ex dx = e-6 ≈ 0,0025.
−∞
Объединяя полученные результаты плотность вероятности СВ η можно записать окончательно в виде
|
|
e−2 (e+ |
y +e− y ) 2 |
|
y при 0 ≤ y ≤ 4 |
Wη ( y ) = |
|
e−2− y 2 |
y +0,0025 |
δ( y −16) при 4 < y ≤16 |
|
|
|||||
|
|
0 |
при прочих |
y |
|
|
|
||||
|
|
|
|
|
|
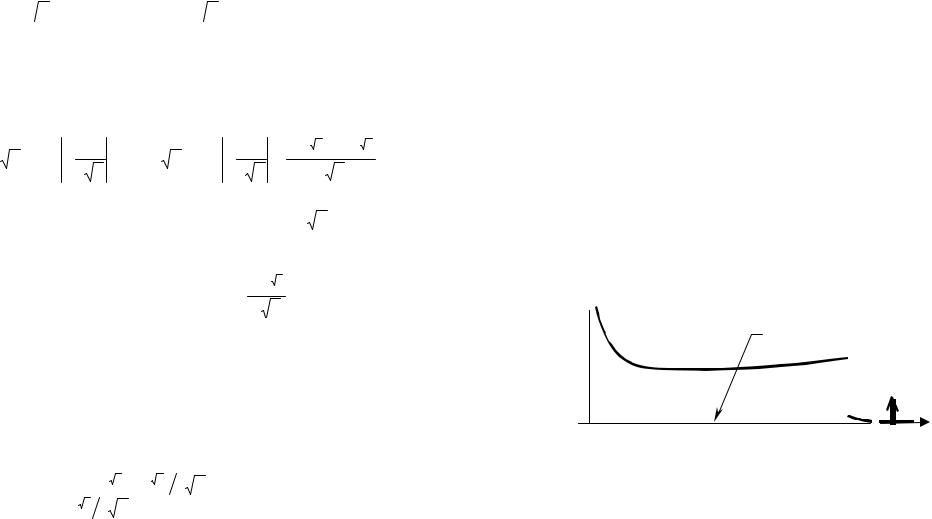
Соответствующий этому выражению график плотности распределения вероятностей представлен на рис. 7.
26
Следует отметить, что на этот раз вычислять числовые характеристики, руководствуясь соотношением (5.3), нецелесообразно, т.к. получаемые интегралы оказываются весьма громоздкими (неудобными). Напротив, при использовании формулы (6.4), дважды применив интегрирование по частям, получаем
|
+∞ |
−6 |
0 |
|
Mη= |
∫f(x)Wξ (x) dx = ∫16 ex dx + ∫ (x + 2)2 ex dx =16 e−6 +(x +2)2 ex |0−6 |
|||
|
−∞ |
−∞ |
−6 |
|
− ∫0 |
2 (x + 2) ex dx =16 e−6 + 4 −16e−6 −2(x + 2) ex |−06 + ∫0 |
2 ex dx = |
||
|
−6 |
|
−6 |
|
= 4 −(4 +8e−6 ) + 2 ex |0−6 = −8 e−6 + 2 − 2 e−6 = 2 −10 e−6 .
Полученный результат хорошо согласуется с полученной выше плотностью вероятности СВ η, так как согласно рис. 7 координата y = Mη ≈ 2 близка к центру масс отображаемой фигуры.
Wз(y)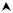
Mз
0,26 























0,2 











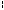
0,0 0,4 0,8 1,2 1,6  2,4 2,8 3,2 3,6 4,0 … 16 x
2,4 2,8 3,2 3,6 4,0 … 16 x
Рис. 7 Плотность вероятности, соответствующая СВ η
27
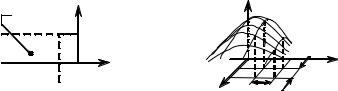
7.СВОЙСТВА СИСТЕМ СЛУЧАЙНЫХ ВЕЛИЧИН
7.1.Вероятностные характеристики
Функцией распределения вероятностей (ФРВ) системы случайных величин ξ и η называют функцию Fξη(x0 , y0 ), определяющую вероятность одновременного выполнения двух неравенств
Fξ η( x0 , y0 ) = P{ ξ < x0 , η < y0 } |
(7.1) |
(на месте запятой в правой части выражения следует подразумевать союз “и”). С геометрических позиций Fξη(x0,y0) определяет вероятность того, что точка со случайными координатами ξ и η попадет на плоскости в нижнюю левую четверть относительно границ x = x0, y = y0.
(ξ,η ) y |
|
Wξη (x,y) |
|
||
|
|
|
|
||
|
y0 |
|
|
x0+dx x |
|
|
|
|
y0 |
||
x0 |
x |
y |
dy |
||
dx |
|||||
|
|
||||
|
|
|
|
||
Рис. 8. Геометрический смысл |
Рис. 9. |
Плотность распре- |
|||
функции распределения |
деления вероятно- |
||||
вероятностей системы СВ |
стей системы СВ |
||||
Как и для отдельных случайных величин, функция распределения вероятностей системы СВ является безразмерной неубывающей функцией всех своих аргументов и принимает значения от нуля до единицы.
Вероятность попадания точки с координатами (ξ, η) в произвольную прямоугольную область может быть рассчитана по формуле
P{x1<ξ≤x2; y1<η≤y2} = Fξη(x2, y2) –Fξη(x2, y1) –Fξη(x1, y2) + Fξη(x1, y1). (7.2)
28
Плотностью распределения вероятностей (ПРВ) систе-
мы случайных величин ξ и η называют функцию Wξη(x,y), характеризующую вероятность принятия в одном и том же опыте величиной ξ значений, близких к аргументу x, а величиной η значений, близких к аргументу y. Численно она определяется отношением вероятности попадания точек с координатами (ξ, η) в бесконечно малый прямоугольник, лежащий около точки (x, y) (см. рис. 9), к площади этого прямоугольника и связана с ФРВ соотношением
Wξη(x,y) = lim |
P{ x ≤ ξ < x + |
x, y ≤η < y + y } |
|
∂2 F |
(x, y) |
. (7.3) |
|
= |
ξη |
|
|||||
|
x y |
|
∂x ∂y |
||||
Λx→0 |
|
|
|||||
Λy→0 |
|
|
|
|
|
|
|
Эта функция неотрицательна и имеет размерность, обратную произведению размерностей величин ξ и η. С ее помощью вероятность попадания точек (ξ, η) в произвольную прямоугольную область может быть рассчитана по правилу
b d
P{ a ≤ ξ < b, с ≤ η < d } = ∫∫ Wξη (x, y) dx dy . (7.4)
a c
Отсюда, в частности, следует, что обратная связь между плотностью и функцией распределения вероятностей имеет вид
y0 x0
Fξη(x0 , y0 ) = P{ ξ < x0 , η < y0 } = ∫ ∫ Wξη (x, y) dx dy . (7.5)
−∞ −∞
Свойство нормировки для плотности распределения вероятностей системы случайных величин приобретает вид
+∞ +∞ |
|
∫ ∫ Wξη (x, y) dx dy = 1 |
(7.6) |
−∞ −∞
и означает, что для любой СВ объем тела под поверхностью ее плотности вероятности всегда равна единице (см. рис. 9).
29

7.2. Числовые характеристики
Двумя основными классами числовых характеристик сис-
тем СВ являются, во-первых, “смешанный начальный момент порядка k, r”
+∞ +∞ |
|
mk r { ξ, η } = ∫ ∫ xk yr Wξη (x, y) dxdy , |
(7.7) |
-∞ -∞
а, во-вторых, “смешанный центральный момент порядка k, r”
+∞ +∞
μk r{ ξ,η } = ∫ ∫ (x − Mξ )k ( y − Mη )r Wξη (x, y) dxdy . (7.8)
-∞ -∞
При k = 0 или r = 0 формулы (7.7), (7.8) преобразуются фактически в (5.3), (5.5) и отражают числовые характеристики СВ ξ и η в отдельности. Первой из специфичных именно для систем СВ числовых характеристик является “смешанный момент порядка 1, 1”. Этот момент называют еще корреляцией величин ξ и η
+∞ +∞ |
|
Bξη = m11 { ξ, η } = ∫ ∫ xy Wξη (x, y) dxdy . |
(7.9) |
-∞ -∞
Нормированным аналогом этой характеристики является коэффициент корреляции между величинами ξ и η, определяемый соотношением
rξη = m11{ ξ, η} - Mξ Mη . |
(7.10) |
Dξ Dη |
|
Коэффициент корреляции характеризует степень линейной взаимосвязи между величинами ξ и η, входящими в систему. Для любых СВ
| rξη | ≤ 1, |
(7.11) |
причем rξη=±1 соответствует жесткой функциональной связи η = k · ξ + b (при k>0 rξη положителен, а при k<0 – отрицателен), значение 0 ≤ | rξη | ≤ 1 свидетельствует о наличии мягкой
30
вероятностной взаимосвязи между величинами, а rξη = 0 говорит о том, что линейная взаимосвязь между величинами ξ и η отсутствует. Подобные величины называют некоррелированными.
Случайные величины, для которых вероятностные характеристики допускают представление
Fξ η(x0 ,y0 ) = Fξ (x0 ) · Fη(y0 ) = P{ ξ ≤ x0 } · P{ η ≤ y0 } или Wξ η(x0 ,y0 ) = Wξ (x0 ) · Wη(y0 )
называют независимыми, поскольку значение, принятое в данном опыте одной из случайных величин, никак не влияет на возможность (способность) принятия конкретных значений другой СВ. Для независимых СВ смешанные начальные моменты любых порядков
+∞ |
+∞ |
mk r {ξ,η}= ∫ |
xk Wξ (x) dx ∫y r Wη( y) dy =mk{ξ}·mr{η}. (7.12) |
-∞ |
-∞ |
Из (7.10) и (7.12) следует, в частности, что независимые случайные величины всегда являются некоррелированными, однако обратное утверждение справедливо далеко не во всех случаях.
При функциональном преобразовании одной системы СВ {ξ1,ξ2} в другую {η1,η2} правило, определяющее взаимосвязь между их законами распределения оказывается аналогичным
(6.1), (6.3) и имеет вид
Wη1η2 ( y1, y2 ) = ∑ Wξ1ξ2 (ϕi1 ( y1, y2 ),ϕi2 ( y1, y2 )) Ji , (7.13)
i
где x1 = φi 1 ( y1, y2 ), x2 = φi 2 ( y1, y2 ) – это обратные к зависимостям y1 = f1( x1, x2 ), y2 = f2( x1, x2 ) функции, позволяющие
рассчитать их аргументы по заданным результатам y1 и y2, а последний сомножитель – это модуль якобиана обратного преобразования, задаваемый определителем
31

∂ϕi1
Ji = ∂∂ϕy1
i2
∂y1
∂ϕi1 |
|
|
|
|
|
|
|||
∂y2 |
|
. |
(7.14) |
|
∂ϕ |
|
|
|
|
i2 |
|
|
|
|
∂y2 |
|
|
|
|
Наиболее часто применяемые случаи функционального преобразования системы случайных величин в новую случайную величину приведены в табл. 7.1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 7.1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вид функцио- |
|
Взаимосвязь законов распределения |
|||||||||||||||
нальной связи |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
|
|
|
|
|
|
|
|
|
|
|
||
η = ξ2 + ξ1 |
|
Wη( y) = ∫Wξ1ξ2 ( u, y −u ) du |
|||||||||||||||
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
+∞ |
|
|
|
|
|
|
|
|
|
|
|
||
η = ξ2 – ξ1 |
|
Wη( y) = ∫Wξ1ξ2 ( u, y + u ) du |
|||||||||||||||
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
+∞ |
|
|
|
|
|
|
|
y |
du |
|||
|
|
Wη( y) = ∫ Wξ1ξ2 |
|
|
|
|
|||||||||||
η = ξ2 · ξ1 |
|
u, |
|
|
|
|
|
||||||||||
|
u |
|
|||||||||||||||
|
|
|
|
|
−∞ |
|
|
|
|
|
|
| u | |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
η = ξ2 / ξ1 |
|
Wη( y) = ∫Wξ1ξ2 ( u, y u ) | u | du |
|||||||||||||||
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fη(y) = Fξ |
1 |
(y) + Fξ |
2 |
(y) − Fξ ξ |
2 |
( y, y) (7.15) |
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
η = min( ξ2 , ξ1 |
) |
+∞ |
|
|
|
|
|
|
+∞ |
|
|
|
|
||||
Wη( y) = |
∫Wξ1ξ2 ( y, x2 ) dx2 |
+ |
|
∫Wξ1ξ2 ( x1, y ) dx1 |
|||||||||||||
|
|
|
|||||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Fη( y) = Fξ ξ |
2 |
( y, y) |
|
|
|
(7.16) |
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
η = max( ξ2 , ξ1 |
) |
|
y |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
Wη( y) = |
∫Wξ1ξ2 ( y, x2 ) dx2 |
+ |
|
∫Wξ1ξ2 ( x1, y ) dx1 |
|||||||||||||
|
|
|
|||||||||||||||
|
|
−∞ |
|
|
|
|
|
|
−∞ |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8. КЛАССИФИКАЦИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
8.1. Краткое теоретическое введение
Случайный процесс (СП) – это численное выражение некоторого явления, протекающего во времени случайным образом. Детерминированные функции, отражающие развитие процесса в отдельном конкретном опыте, называются его реализациями. Таким образом, случайный процесс ξ(t) можно
представлять себе как совокупность всех его возможных реа-
лизаций ξ(1)(t), ξ(2)(t), … ξ(n)(t).
Случайные процессы, свойства которых изменяются во времени произвольным образом, называются нестационарными. Процессы, свойства которых не зависят от момента начала отсчета времени и остаются неизменными вдоль всей временной оси, называются стационарными. Наконец, стационарные процессы, состоящие лишь из однотипных реализаций, называются эргодическими. (Более строгие определения различных классов СП можно найти в [3, 4], но для решения практических задач важнее обратить внимание на особенности “поведения” характеристик процессов различных классов).
8.1.1. Одномерная функция распределения СП
Для процессов общего вида (нестационарных) одномерная функция распределения характеризует вероятность наблюдения реализаций СП, проходящих в заданный момент времени t ниже заданного порога x
Fξ (x;t) = P{ ξ(t) < x }. |
(8.1) |
У стационарных процессов подобная вероятность остается неизменной вдоль всей временной оси, а потому аргумент t оказывается избыточным
Fξ (x;t) = Fξ (x) . |
(8.2) |
33

И, наконец, для процессов эргодических эта вероятность проявляет себя в виде среднего времени, которое каждая из реализаций данного СП проводит ниже уровня x
F (x;t) = |
lim |
T [ξ(i) (t) < x] |
. |
(8.3) |
|
ξ |
T |
→∞ |
Tнабл |
|
|
|
набл |
|
|
|
|
Следует иметь в виду, что по отношению к аргументу x остаются справедливыми все свойства функция распределения, разобранные в разделе 4. Что же касается аргумента t, то в расчетных формулах он не участвует, выступая лишь как “внешний” параметр, определяющий к какому моменту времени относятся анализируемые характеристики.
8.1.2. Одномерная плотность вероятностей СП
Одномерная плотность вероятностей характеризует возможность наблюдения реализаций СП, в заданный момент времени t принимающих значения близкие к аргументу x, и определяется отношением вероятности попадания значений
реализации процесса |
ξ(t) в бесконечно малую окрестность |
||||||
аргумента x к ширине этой окрестности |
|
||||||
W (x;t) = |
lim |
P{ x ≤ ξ(t) < x + |
x } |
= |
∂Fξ (x;t) |
. |
(8.4) |
|
|
|
|||||
ξ |
x→0 |
x |
|
|
∂x |
|
|
|
|
|
|
||||
И вновь для стационарных процессов аргумент |
t в (8.4) |
||||||
может быть опущен, а для каждой реализации эргодического СП плотность вероятности будет показывать отношение час-
тоты наблюдения значений из интервала [ x; x + |
|
x ] к ширине |
||
этого интервала |
x |
|
|
|
W (x;t) = |
lim T [x≤ξ(i) (t) < x+ |
x] |
. |
(8.5) |
ξ |
x→0 |
x Tнабл |
|
|
|
Tнабл→∞ |
|
|
|
|
34 |
|
|
|
8.1.3. Математическое ожидание СП
Для процессов общего вида характеризует зависимость от времени среднего арифметического значений разных реализаций, наблюдаемых в момент t,
+∞ |
|
Mξ (t) = ∫ x Wξ (x;t) dx . |
(8.6) |
−∞
Среднее значение определяется применительно ко всей совокупности возможных реализаций.
Свойства стационарных процессов остаются неизменными вдоль всей временной оси, поэтому математическое ожидание таких процессов является константой по отношению к аргументу t. Для эргодических процессов эта константа совпадает со средним по времени значением – постоянной составляющей – любой из реализаций
|
|
|
|
|
|
1 |
|
+Tнабл / 2 |
|
|||
M |
ξ |
(t) = M |
ξ |
= |
lim |
|
∫ |
ξ(i) (t) dt = ξ(i) . |
(8.7) |
|||
|
||||||||||||
|
|
|
Tнабл→∞ T |
|
|
_ |
|
|||||
|
|
|
|
|
|
набл |
|
−T |
|
/ 2 |
|
|
|
|
|
|
|
|
|
|
набл |
|
|
||
8.1.4. Дисперсия случайного процесса
Характеризует разброс значений, принадлежащих различным реализациям, относительно математического ожидания
+∞ |
|
Dξ (t) = ∫(x − Mξ (t))2 Wξ (x;t) dx . |
(8.8) |
−∞
Для стационарных СП дисперсия от времени не зависит, а для процессов эргодических она совпадает со средней мощностью переменной составляющей любой из реализаций СП
Dξ (t) = Dξ = lim |
1 |
|
+Tнабл / 2 |
(ξ(i) (t) − ξ(i) )2 dt = P |
(i) . (8.9) |
|
∫ |
||||
Tнабл→∞ T |
|
~ ξ |
|
||
|
набл |
|
−T / 2 |
|
|
|
|
|
набл |
|
|
|
|
|
35 |
|
|
Полезно иметь в виду, что определяемые (8.3), (8.5), (8.7), (8.9) свойства являются проявлением единого принципа: любая характеристика эргодического СП может быть получена путем соответствующего усреднения по времени (на интервале бесконечной протяженности) произвольной реализации этого процесса. Тот же самый принцип можно выразить и иначе: для эргодических процессов “среднее по времени” любой из реализаций совпадает со “средним по ансамблю реализаций процесса”.
8.2. Типовые задачи
Задача 1. Случайное напряжение характеризуется плотностью вероятности
|
1 |
|
(x - 2 t) |
2 |
|
|
|
W (x;t) = |
|
|
|
, 1/В. |
(8.10) |
||
2 2π |
exp - |
4 |
|
|
|||
ξ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Каковы возможные реализации данного случайного процесса? Решение
а) Отметим сразу, что имеющейся в данной задаче информации о процессе ξ(t) недостаточно для прогнозирования формы его реализаций, т.к. одномерная плотность вероятности (8.10) характеризует ситуацию лишь в отдельных временных сечениях, но не содержит сведений о динамичности изменения процесса во времени. Таким образом, может существовать огромное множество процессов, соответствующих (8.10), с существенно отличающимися реализациями.
б) Определяемый (8.10) закон распределения соответствует нормальной (гауссовской) плотности вероятности
|
1 |
|
(x - a) |
2 |
|
|
|
Wξ (x) = |
|
|
|
(8.11) |
|||
2π σ |
exp - |
2 σ |
2 |
|
. |
||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
с параметрами a = 2·t (В), σ = 2 (В). Параметр a изменяется во времени, что указывает на нестационарный характер исследуемого процесса. Так как параметр a определяет математи-
36
ξ(i)(t), В Mξ(t)+3·σ Mξ(t)
12
6 |
Mξ(t)-3·σ |
–3 |
3 |
6 t, с |
– 6
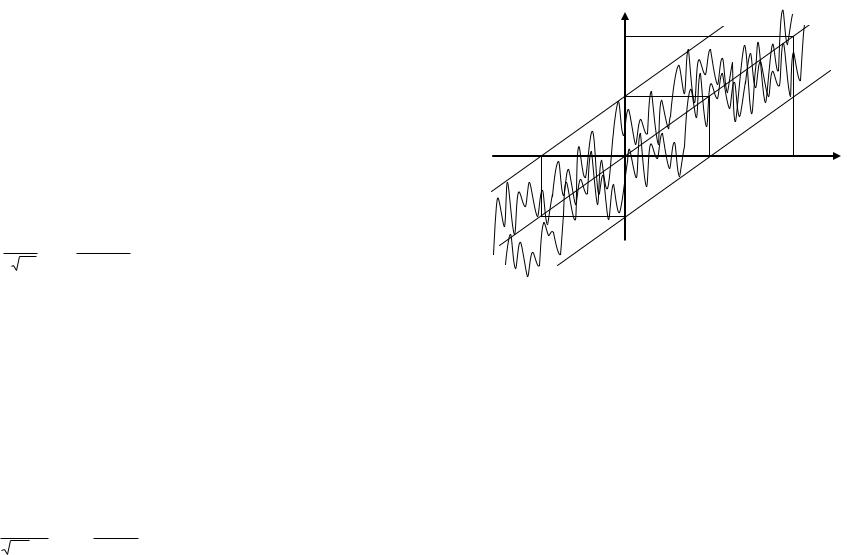
Рис. 10. Возможные реализации СП из задачи 1
ческое ожидание нормального распределения, то характерной особенностью реализаций исследуемого СП будет линейное нарастание их среднего значения с течением времени Mξ(t) = = 2·t (В). Несколько подобных функций – возможных реализаций процесса ξ(t) – показано на рис. 10. При их построении было учтено правило “3 сигм”, утверждающее, что для подавляющего большинства случайных величин (процессов) мгновенные значения могут отклоняться от математического ожидания не более чем на три эффективных значения σ.
Задача 2. Реализации эргодического СП, представляют собой последовательность однополярных импульсов напряжения с амплитудой U = 3 В (рис. 11). Ширина и положение импульсов на оси времени изменяются хаотично, но среднее время, суммарно занимаемое импульсами каждой реализации, составляет 40 %. Какой дисперсией будет характеризоваться данный СП в момент времени t = 5 мс?
37
