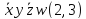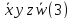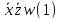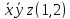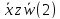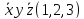курс дискрет готовый
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
(ФГБОУ ВПО «ВГТУ», ВГТУ)
Факультет информационных технологий и компьютерной безопасности
(факультет)
Кафедра Математики
КУРСОВАЯ РАБОТА
по дисциплине: Дискретная математика .
Тема: Приложении дискретной математики к задачам информационных технологий. Вариант 3. .
Расчетно-пояснительная записка
Разработал студент Григоров А.И.
Подпись, дата Инициалы, фамилия
Руководитель Ююкин Н.А.
Подпись, дата Инициалы, фамилия
Защищена ____________________ Оценка _____________________________
дата
2014
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
(ФГБОУ ВПО «ВГТУ», ВГТУ)
Кафедра КИТП
ЗАДАНИЕ
на курсовую работу
по дисциплине Дискретная математика .
Тема работы Приложении дискретной математики к задачам информационных технологий. Вариант 3. .
Студент группы ИСТ-142 Григоров Артём Игоревич .
Фамилия, имя, отчество.
Сроки выполнения этапов .
Сроки защиты курсовой работы .
Руководитель . Ююкин Н.А. ..
Подпись дата Фамилия, инициалы
Задание принял студент . Григоров А.И .
Подпись дата Фамилия, инициалы
Замечания руководителя
Содержание:
Введение………………………………………………………………………………...5
-
Теоретическая часть………………………………………………………………...6
-
Основные определения…………………………………………………………….6
-
Анализ связей, отношений, операций темы и их применение к задачам информационных систем и технологий…………………………………………11
-
Роль излагаемой темы в задачах информационных систем и технологий……13
-
-
Практическая (расчётная) часть…………………………………………………..13
Список литературы……………………………………………………………………22
Введение
Дискретная математика – область математики, изучающая дискретные математические объекты и структуры. Её элементы возникли в глубокой древности. С незапамятных времен известны комбинаторно-логические задачи, решение которых связано с перебором комбинаций дискретных объектов и логическим анализом возникающих вариантов.
В широком смысле дискретная математика включает в себя такие давно сложившиеся разделы математики, как теория чисел, алгебра, теория множеств, математическая логика и другие. В узком смысле дискретная математика состоит из ряда специальных разделов и сравнительно новых разделов, которые интенсивно стали развиваться с середины прошлого века в связи с изобретением и постепенным внедрением во все сферы жизни ЭВМ и цифровых технологий. К таким разделам можно отнести теорию функциональных систем, теорию графов и сетей, комбинаторный анализ, теорию автоматов и алгоритмов, теорию кодирования, теорию синтеза управляющих систем, дискретную геометрию и др.
Бурное развитие дискретной математики во второй половине XX века связывают с «цифровой революцией» в телекоммуникационной и вычислительной технике. Дискретная математика стала основой проектирования и применения многочисленных цифровых электронных устройств. Возникновение в рамках кибернетики математической теории управляющих систем привело к развитию целых новых разделов дискретной математики: теории сложности, теории тестов, теории надежности схем, теории автоматов и других. Существенный вклад в дискретную математику на этом этапе был сделан Дж. фон Нейманом, А.А. Ляпуновым, С.В. Яблонским, О.Б. Лупановым.
Начиная с середины XX в. в нашу жизнь бурно вошли и вскоре заняли доминирующее место информационные системы и технологии различного назначения. Дискретная математика, в частности её раздел – теория множеств, который будет рассмотрен подробно в данной курсовой работе, играет очень большую роль при решении задач информационных систем и технологий.
1. Теоретическая часть.
1.1 Основные определения.
Понятие нечеткого множества.
Понятие нечеткого множества - эта попытка математической формализации нечеткой информации для построения математических моделей. В основе этого понятия лежит представление о том, что составляющие данное множество элементы, обладающие общим свойством, могут обладать этим свойством в различной степени и, следовательно принадлежать к данному множеству с различной степенью. При таком подходе высказывания типа “такой-то элемент принадлежит данному множеству” теряют смысл, поскольку необходимо указать “насколько сильно” или с какой степенью конкретный элемент удовлетворяет свойствам данного множества.
Нечетким
множеством 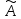 на
универсальном множестве U называется
совокупность пар (
на
универсальном множестве U называется
совокупность пар ( ),
где
),
где 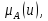 -
степень принадлежности элемента u
-
степень принадлежности элемента u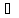 U к
нечеткому множеству
U к
нечеткому множеству 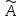 .
Степень принадлежности - это число
из диапазона [0, 1]. Чем выше степень
принадлежности, тем в большей мерой
элемент универсального множества
соответствует свойствам нечеткого
множества.
.
Степень принадлежности - это число
из диапазона [0, 1]. Чем выше степень
принадлежности, тем в большей мерой
элемент универсального множества
соответствует свойствам нечеткого
множества.
Функция принадлежности.
Функцией принадлежности называется функция, которая позволяет вычислить степень принадлежности произвольного элемента универсального множества к нечеткому множеству.
Если
универсальное множество состоит из
конечного количества элементов U=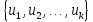
![]() ,
тогда нечеткое множество
,
тогда нечеткое множество 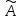 записывается
в виде
записывается
в виде
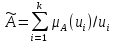 .
В случае непрерывного множества U
используют такое обозначение
.
В случае непрерывного множества U
используют такое обозначение
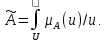
Основные операции над нечеткими множествами и их свойства.
Включение.Пусть А и В —
нечеткие множества на универсальном
множестве Е. Говорят,
что А содержится
в В,если
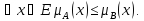
Обозначение: А ⊂ В.
Иногда используют термин доминирование, т.е. в случае, когда А ⊂ В,говорят, что В доминирует А.
Равенство.А
и В равны, если
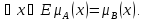
Обозначение: А = В.
Дополнение.Пусть М =
[0, 1], А и В –
нечеткие множества, заданные на Е.
А и В дополняют
друг друга, если
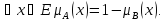
Обозначение:
B=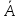 или A=
или A=
Очевидно,
что 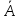 =A (дополнение
определено для М =
[0, 1], но очевидно, что его можно определить
для любого упорядоченного М).
=A (дополнение
определено для М =
[0, 1], но очевидно, что его можно определить
для любого упорядоченного М).
Пересечение. А ⋂ В— наибольшее нечеткое подмножество, содержащееся одновременно в А и В:
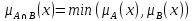 .
.
Объединение. A∪В — наименьшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности:
 .
.
Разность.A-B=A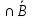 с
функцией принадлежности:
с
функцией принадлежности:
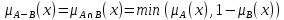
Дизъюнктивная сумма
А ⊕ В = (A - B) ∪ (B - A) = (A ⋂ ̅B) ∪ ( ̅A ⋂ B)
с функцией принадлежности:
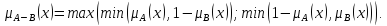
Для операций объединения и пересечения выполняются следующие свойства:
-
Идемпотентность
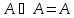
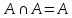
-
Коммутативность
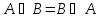
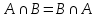
-
Ассоциативность
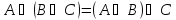
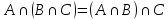
-
Дистрибутивность
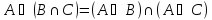
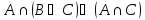
-
Поглощение
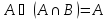
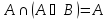
-
Свойство нуля
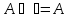
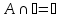
-
Свойство единицы

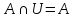
-
Инволютивность

-
Законы де Моргана
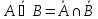
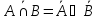
-
Дополнительность
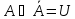
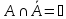
Расстояние между нечеткими множествами и индексы нечеткости.
Пусть A , B и C – конечные нечеткие множества, заданные на универсальном множестве X . Введем понятие расстояния ρ A , B между нечеткими множествами. При введении расстояния обычно предъявляются следующие требования:
ρ A , B ≥ 0 – неотрицательность;
ρ A , B = ρ B , A – симметричность;
ρ A , B ≤ ρ A , C + ρ B , C – транзитивность;
ρ A , A = 0 – самоподобие.
Расстояние Хемминга(линейное расстояние) определяется как:
ρ A , B = ∑ i = 1 n μ A x i − μ B x i , 0 ≤ ρ A , B ≤ n .
Относительное расстояние Хемминга определяется как:
ρ rel A , B = 1 n ∑ i = 1 n μ A x i − μ B x i = 1 n ρ A , B , 0 ≤ ρ rel A , B ≤ 1 .
Евклидово (квадратичное расстояние) определяется как:
e A , B = ∑ i = 1 n μ A x i − μ B x i 2 , 0 ≤ e A , B ≤ n .
Относительное Евклидово расстояние определяется как:
e rel A , B = 1 n ∑ i = 1 n μ A x i − μ B x i 2 = e A , B n , 0 ≤ e rel A , B ≤ 1 .
Перейдем к индексам нечеткости или показателям размытости нечетких множеств.
Если объект х обладает свойством R (порождающим нечеткое множество A) лишь в частной мере, т.е.
0<μA(x)<1, то внутренняя неопределенность, двусмысленность объекта х в отношении R проявляется в том, что он, хотя и в разной степени, принадлежит сразу двум противоположным классам: классу объектов, "обладающих свойством R", и классу объектов, "не обладающих свойством R". Эта двусмысленность максимальна, когда степени принадлежности объекта обеим классам равны, т.е. μA(x) = (x) = 0,5, и минимальна, когда объект принадлежит только одному классу, т.е. либо μA(x) = 1 и (x) = 0, либо μA(x) = 0 и (x) = 1.
В общем случае показатель размытости нечеткого множества можно определить в виде функционала d(A) со значениями в R (положительная полуось), удовлетворяющего условиям:
d(A) = 0 тогда и только тогда, когда А - обычное множество;
d(A) максимально тогда и только тогда, когда μA(x) = 0.5 для всех x∈E.
d(A)d(B), если A является заострением B, т.е.
μA(x)≤μB(x) при μB(x) < 0,5;
μA(x)≥μB(x) при μB(x) > 0,5;
μA(x)- любое при μB(x) = 0,5.
d(A) = d() - симметричность по отношению к 0,5.
d(A∪B)+d(A∩B) = d(A)+d(B).
Декомпозиция нечетких множеств.
Одно
из важнейших свойств нечетких
отношений заключается
в том, что они могут быть представлены
в виде совокупности обычных отношений,
причем могут быть упорядочены по
включению, представляя собой иерархическую
совокупность отношений. Разложение нечеткого
отношения на
совокупность обыкновенных отношений
основано на понятии  -уровня нечеткого
отношения.
Здесь для простоты будем полагать,
что L линейно
упорядочено.
-уровня нечеткого
отношения.
Здесь для простоты будем полагать,
что L линейно
упорядочено.
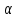 -уровнем нечеткого
отношения R называется
обычное отношение
-уровнем нечеткого
отношения R называется
обычное отношение 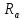 ,
определяемое для всех
,
определяемое для всех 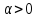 следующим
образом:
следующим
образом:
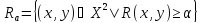
Очевидно,
что  -уровни нечетких
отношений удовлетворяют
соотношению:
-уровни нечетких
отношений удовлетворяют
соотношению:

представляя собой совокупность вложенных друг в друга отношений.
Теорема. Нечеткое
отношение R обладает
каким-либо тогда и только тогда, если
этим свойством обладают все его 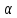 -уровни.
-уровни.
1.2 Анализ связей, отношений, операций темы и их применение к задачам информационных систем и технологий.
Теория множеств — один из краеугольных камней математики, обеспечивающий удобный язык для описания массы концепций как в математике, так и в и информатике.
В современных языках программирования требуется, чтобы переменные объявлялись как принадлежащие к определенному типу данных. Тип данных представляет собой множество объектов со списком стандартных операций над ними. Определение типа переменных равносильно указанию множества, из которого переменным присваиваются значения.
Операция прямого произведения множеств имеет практическое значение, поскольку вплотную подводит к понятиям «отношение» и «функция», играющим заметную роль в информатике.
В основе нечеткой логики лежит теория нечетких множеств, где функция принадлежности элемента множеству не бинарна (да/нет), а может принимать любое значение в диапазоне 0-1. Это дает возможность определять понятия, нечеткие по самой своей природе: "хороший", "высокий", "слабый" и т.д. Нечеткие множества позволяют выполнять над такими величинами весь спектр логических операций: объединение, пересечение, отрицание и др. Нечеткие множества дают возможность строить базы знаний и экспертные системы нового поколения, способные хранить и обрабатывать неточную информацию.
Другая область применения нечетких множеств - электронные системы различного назначения, от систем оценки глобального загрязнения атмосферы и предсказания землетрясений до АСУ заводских цехов и технологических процессов. По сравнению с традиционными методами анализа и вероятностным подходом методы нечеткого управления позволяют быстро производить анализ задачи и получать результаты с высокой точностью.
После постановки задачи в терминах правил, состоящих из условий и выводов, производится их обработка по специальным алгоритмам. Идея обработки состоит в преобразовании нечетких значений условий и выводов в количественную форму. Для этого используются различного рода функции принадлежности: треугольные, трапецеидальные, колоколообразные и другие. Выбор типа функции зависит от решаемой задачи.
1.3 Роль излагаемой темы в задачах информационных систем и технологий.
Таким образом, можно утверждать, что данная тема играет важную роль в решении задач информационных систем и технологий. Связи, отношения и операции, рассмотренные выше активно используются при работе, связанной с хранением данных на компьютерах. Так же эти связи и операции используются при работе с языками программирования, в частности в работе с базами данных. Они позволяют определить тип данных в языках программирования, создавать базы данных и системы управления ими, участвуют в различных сортирующих процедурах.
2. Практическая (расчётная) часть.
Минимизация систем частично определённых булевых функций (Расчёт цифровых устройств комбинационного типа).
Задание:
Известны алгоритмы функционирования ряда комбинационных цифровых устройств, определяющих связь между их входными и выходными сигналами. Эти связи задаются таблицами истинности, входные параметры которых x,y, z,w имеют стандартный вид, а векторы-строки выходных переменных f, этих переменных записаны в таблице.
|
|
|
|
|
0 |
0 |
0 |
|
- |
0 |
0 |
|
1 |
- |
0 |
|
1 |
1 |
- |
|
1 |
1 |
1 |
|
- |
1 |
1 |
|
0 |
- |
1 |
|
0 |
0 |
- |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
Необходимо спроектировать систему, объединяющую три логических устройства, и отличающуюся минимум логических элементов. Изобразить эту схему графически, используя условные обозначения логических элементов.
Решение.
Составим таблицу истинности:
|
x |
y |
z |
w |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
- |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
- |
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
- |
|
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
- |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
- |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
- |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1) Найдём СДНФ. Для этого минимизируем ДНФ.
А)
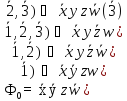 .
.
Б)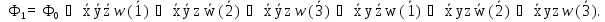
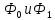 – СДНФ.
– СДНФ.
2)
Теперь найдём сокращённую
 .
.
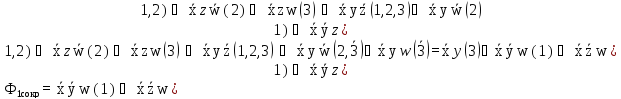
Для получения минимальной ДНФ необходимо убрать из сокращённой ДНФ все лишние простые импликанты. Для этого составим импликантную матрицу Квайна.
3) Матрица импликантности:
|
|
|
|
|
|
|
|
|
|
|
*(3) |
*(3) |
*(3) |
|
|
|
*(1) |
|
|
|
|
|
*(1) |
*(1,2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*(1,2,3) |
*(2,3) |
|
|
|
|
|
*(2) |
|
|

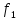
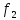
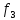
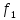
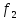
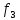
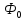
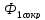
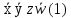
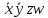 (1,2)
(1,2)