2.14.Деление отрезка в заданном отношении.
Т ребуется
разделить отрезок АВ,
соединяющий точки А(х1;у1)
и B(x2;y2)
в заданном отношении
ребуется
разделить отрезок АВ,
соединяющий точки А(х1;у1)
и B(x2;y2)
в заданном отношении
 >
0, т.е. найти координаты точки М(х;у)
отрезка АВ
такой, что
>
0, т.е. найти координаты точки М(х;у)
отрезка АВ
такой, что
 (см. рис.).
(см. рис.).
Решение:
Введем в рассмотрение векторы
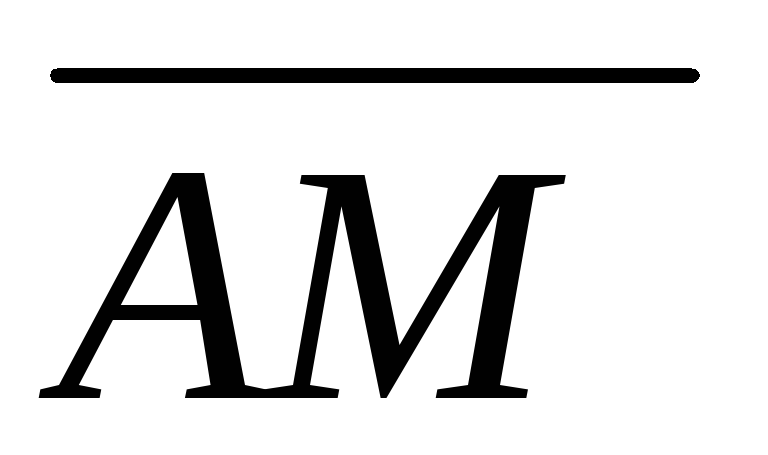 и
и
 .
Точка М
делит отрезок АВ
в отношении
.
Точка М
делит отрезок АВ
в отношении
 ,
если
,
если
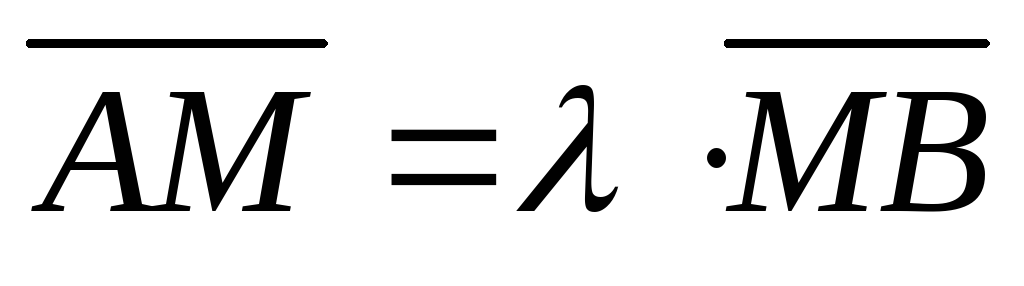 .
(1)
.
(1)
Но
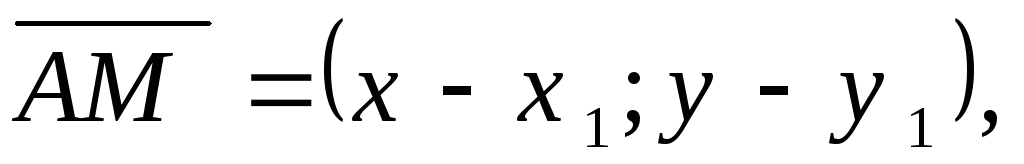 т.е.
т.е.
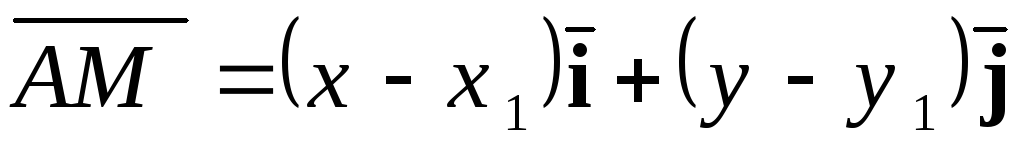 и
и
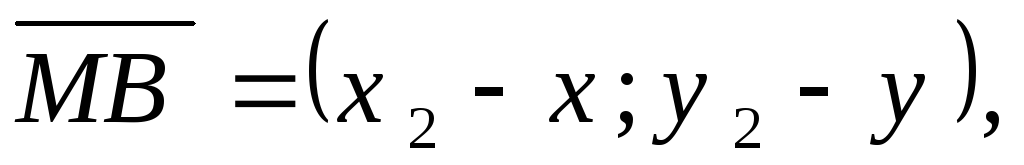 т.е.
т.е.
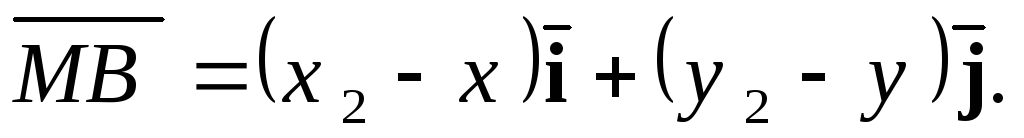
Уравнение
(1) принимает вид
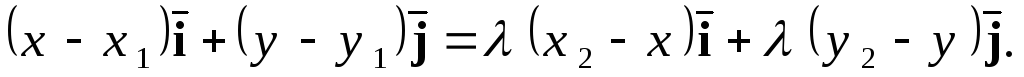
Учитывая,
что равные векторы имеют равные
координаты, получаем
 т.е.
т.е.
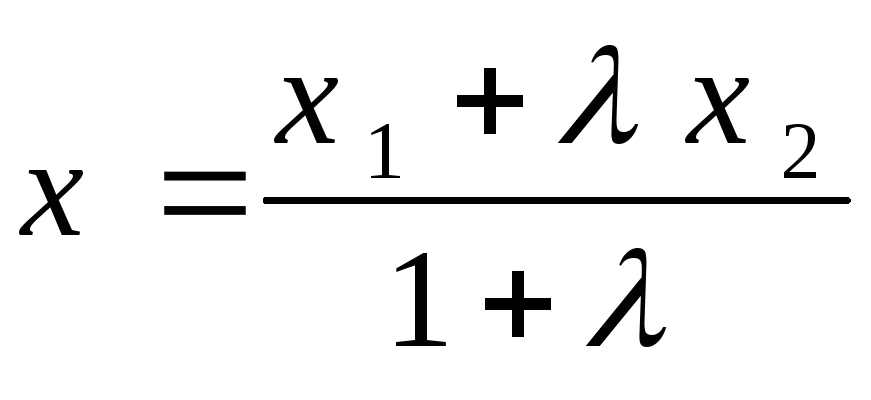
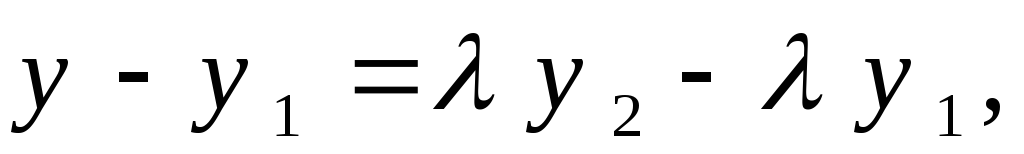 т.е.
т.е.
 (2)
(2)
Формулы
(2) и (3) называются формулами
деления отрезка в данном отношении.
В частности, при
 =1,
т.е. если АМ=МВ, получаем координаты
точки, делящей отрезок пополам
=1,
т.е. если АМ=МВ, получаем координаты
точки, делящей отрезок пополам
 ,
,
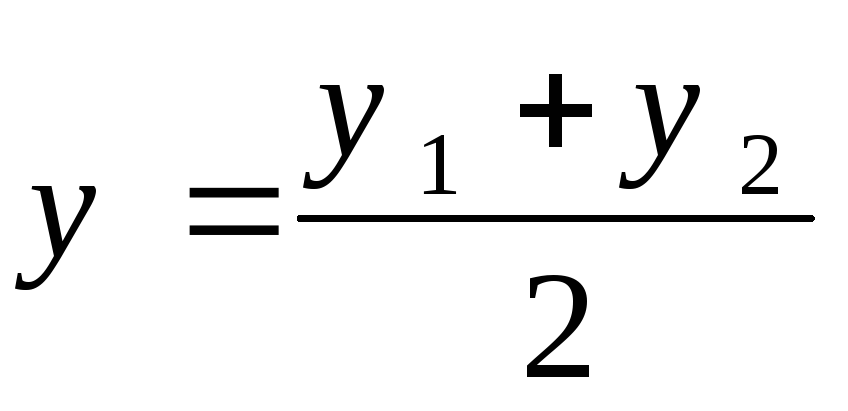 .
В этом случае точка М(х;
у) является
серединой
отрезка АВ.
.
В этом случае точка М(х;
у) является
серединой
отрезка АВ.
Замечание:
Если
 = 0, то это означает, что точки А
и М
совпадают, если
= 0, то это означает, что точки А
и М
совпадают, если
 < 0, то точка М
лежит вне отрезка АВ
— говорят,
что точка М
делит отрезок
АВ
внешним образом .
< 0, то точка М
лежит вне отрезка АВ
— говорят,
что точка М
делит отрезок
АВ
внешним образом .


 ребуется
разделить отрезок АВ,
соединяющий точки А(х1;у1)
и B(x2;y2)
в заданном отношении
ребуется
разделить отрезок АВ,
соединяющий точки А(х1;у1)
и B(x2;y2)
в заданном отношении