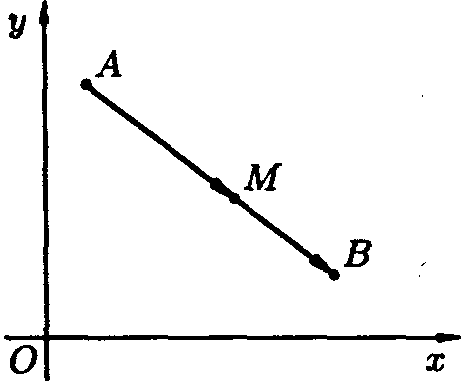
2.14. Деление отрезка в заданном отношении.

Требуется разделить отрезок АВ, соединяющий точки А(х₁;у₁)и B(x₂;y₂) в заданном отношении  > 0, т.е. найти координаты точки М(х;у) отрезка АВ такой, что

Решение: Введем в рассмотрение векторы и . Точка М делит отрезок АВ в отношении , если

. (1)

Но т.е. и т.е. Уравнение (1) принимает вид

Учитывая, что равные векторы имеют равные координа­ты, получаем

т.е. (2)

т.е. (3)

Формулы (2) и (3) называются формулами деления от­резка в данном отношении. В частности, при т.е. если АМ=МВ, то они примут вид , . В этом случае точка М(х; у) является серединой отрезка АВ.

Замечание: Если  = 0, то это означает, что точки А и М совпадают, если  < 0, то точка М лежит вне отрезка АВ — говорят, что точка М делит отрезок АВ внешним образом (-1 , т. к. в противном случае т. е. AM + MB = 0, т. е. АВ = 0).

Пример 1. Даны точки А (-3, 1) и В (2, 4). В каком отношении ось Оy делит отрезок АВ?

Решение. Пусть ось Оy пересекает отрезок АВ в точке С.

Ее координаты ( 0, у). Координаты концов отрезка

Пример 2 Найти координаты центра масс треугольника АВС, если известны координаты его вершин: А (-4, -2); В (2, 0); С (1, 3).

Решение. Искомая точка лежит на пересечении его медиан. Найдем координаты точки D - середины стороны АВ:

Известно, что медианы треугольника пересекаются в точке М, которая делит медиану AD в отношении 1/2

Следовательно, .

Задания для самостоятельного решения

1. Определить, какой является тройка (правой или левой), если

1) ; 2)

3) .

2. Векторы , образующие правую тройку, взаимно перпендикулярны. Зная, что , вычислить .

3. Даны векторы { 1; -1; 3}, {-2; 2; 1}, { 3; -2; 5}. Вычислить.

4. Установить компланарны ли векторы , если

1) { 2; 3; -1}, {1; -1; 3}, { 1; 9; 11};

2) {3; -2; 1}, {2; 1; 2}, { 3; -1; -2};

3) {2; -1; 2}, {1; 2; -3}, { 3; -4; 7}.

5. Доказать, что точки A (1; 2; -1), B (0; 1; 5), C (-1; 2; 1), D(2; 1; 3) лежат в одной плоскости.

6. Вычислить объем параллелепипеда, построенного на векторах.

7. Вычислить объем тетраэдра, вершины которого находятся в точках A (5, 2, 2), B(-8, -2, 5), C(6, 3, 0), D(9, 3,2).

8.­ Вычислить объем тетраэдра, вершины которого находятся в точках A (2; -1; 1), B (5; 5; 4), C (3; 2; -1),

D (4; 1; 3).

9. Даны вершины тетраэдра A (2; 3; 1), B (4; 1; -2), C (6; 3; 7), D (-5; -4; 8). Найти длину его высоты, опущенной из вершины D.

10. Объем тетраэдра v = 5, три его вершины находятся в точках A (2; 1; -1), B (3; 0; 1), C (2; -1; 3). Найти координаты четвертой вершины D, если известно, что она лежит на оси Оу.

Ответы: 1. 1) Правая; 2) левая; 3) левая. 2. = 24.

3. = 0,5. 4. 1) Компланарны; 2) не компланарны; 3) компланарны. 6. 43. 7. 0,5. 8. 3. 9. 11. 10.

11.Заданы четыре точки:

, , , .

1) Проверить, что эти точки будут вершинами некоторой пирамиды и найти объем этой пирамиды.

2) Найти проекцию вектора на направление вектора .

3) Найти угол .

4) Найти площадь грани .

5) Найти векторное произведение и скалярное произведение векторов и .

Если точки заданы координатами:

1.