11

Лекция№6

2.11. Смешанное произведение векторов

Рассмотрим произведение векторов , и , составленное следующим образом: . Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.

Выясним геометрический смысл выражения .

Теорема. Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.

Доказательство..Построим параллелепипед, ребрами которого являются векторы , , и вектор .

Имеем: , , где - площадь параллелограмма, построенного на векторах и , для правой тройки векторов и для левой, где - высота параллелепипеда. Получаем: , т.е. , где - объем параллелепипеда, образованного векторами , и .

Свойства смешанного произведения

1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т.е. .

Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер.

2. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения, т.е. .

Действительно, и . Знак в правой части этих равенств берем один и тот же, так как тройки векторов , , и , , - одной ориентации.

Следовательно, . Это позволяет записывать смешанное произведение векторов в виде без знаков векторного, скалярного умножения.

3. Смешанное произведение меняет знак при перемене мест любых двух векторов-сомножителей, т.е. , , .

Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.

4. Смешанное произведение ненулевых векторов , и равно нулю тогда и только тогда, когда они компланарны.

2.12. Вычисление смешанного произведения в координатной форме в ортонормированном базисе

Пусть заданы векторы , , . Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:

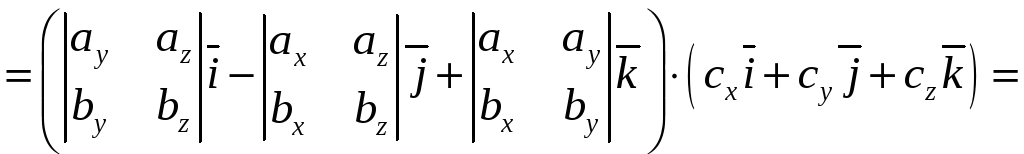
. (10)

Полученную формулу можно записать короче:

,

так как правая часть равенства (10) представляет собой разложение определителя третьего порядка по элементам третьей строки.

Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.

2.13.Некоторые приложения смешанного произведения

Определение взаимной ориентации векторов в пространстве

Определение взаимной ориентации векторов , и основано на следующих соображениях. Если , то , , - правая тройка; если , то , , - левая тройка.

Условие компланарности векторов

Векторы , и компланарны тогда и только тогда, когда их смешанное произведение равно нулю (, , ):

векторы , , компланарны.

Определение объемов параллелепипеда и треугольной пирамиды

Нетрудно показать, что объем параллелепипеда, построенного на векторах , и вычисляется как , а объем треугольной пирамиды, построенной на этих же векторах, равен .

Пример 1. Доказать, что векторы , , компланарны.

Решение. Найдем смешанное произведение этих векторов по формуле:

.

. Это и означает, что векторы компланарны.

Пример 2. Даны вершины тетраэдра: (0, -2, 5), (6, 6, 0), (3, -3, 6), (2, -1, 3). Найти длину его высоты, опущенной из вершины .

Решение. Найдем сначала объем тетраэдра . По формуле получаем:

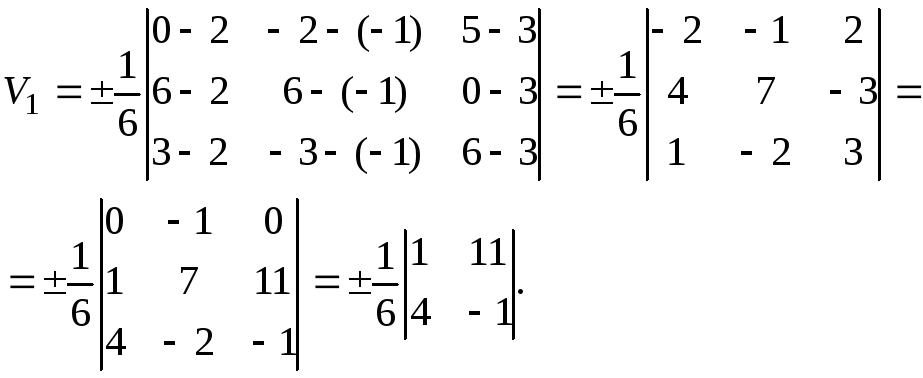
Так как определитель равен отрицательному числу, то в данном случае перед формулой нужно взять знак минус. Следовательно, .

Искомую величину h определим из формулы , где S – площадь основания. Определим площадь S:

где

Поскольку

то

Подставляя в формулу значения и , получим h=3.

Пример 3. Образуют ли векторы базис в пространстве ? Разложить вектор по базису векторов .

Решение. Если векторы образуют базис в пространстве, то они не лежат в одной плоскости, т.е. являются некомпланарными. Найдем смешанное произведение векторов : ,

Следовательно, векторы не компланарны и образуют базис в пространстве. Если векторы образуют базис в пространстве, то любой вектор можно представить в виде линейной комбинации базисных векторов, а именно ,где координаты вектора в базисе векторов . Найдем эти координаты, составив и решив систему уравнений

.

Решая ее методом Гаусса, имеем

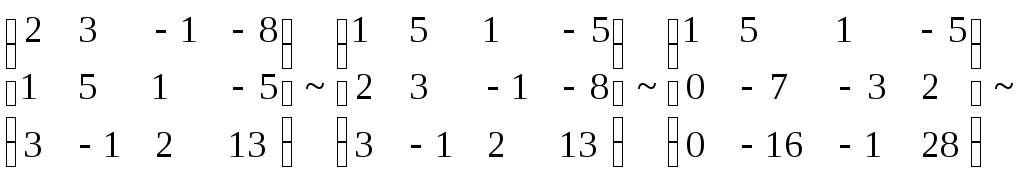
Отсюда . Тогда .

Таким образом, .

Пример 4. Вершины пирамиды находятся в точках: , , , . Вычислить:

а) площадь грани ;

б) объем пирамиды ;

в) проекцию вектора на направление вектора ;

г) угол ;

д) проверить, что векторы , , компланарны.

Решение

а) Из определения векторного произведения известно, что:

.

Находим векторы и , используя формулу

;

, .

Для векторов, заданных своими проекциями, векторное произведение находится по формуле

, где .

Для нашего случая

.

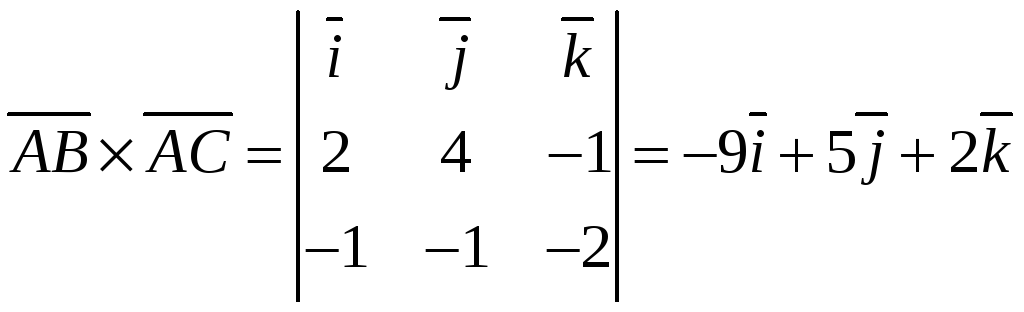Длину полученного вектора находим, используя формулу

, .

и тогда (кв. ед.).

б) Смешанное произведение трех векторов по абсолютной величине равно объему параллелепипеда, построенного на векторах , , как на ребрах.

Смешанное произведение вычисляется по формуле:

.

Найдем векторы , , , совпадающие с ребрами пирамиды, сходящимися к вершине :

,

,

.

Смешанное произведение этих векторов

.

Так как объем пирамиды равен части объема параллелепипеда, построенного на векторах , , , то (куб. ед.).

в) Используя формулу , определяющую скалярное произведение векторов , , можно записать так:

,

где или ;

или .

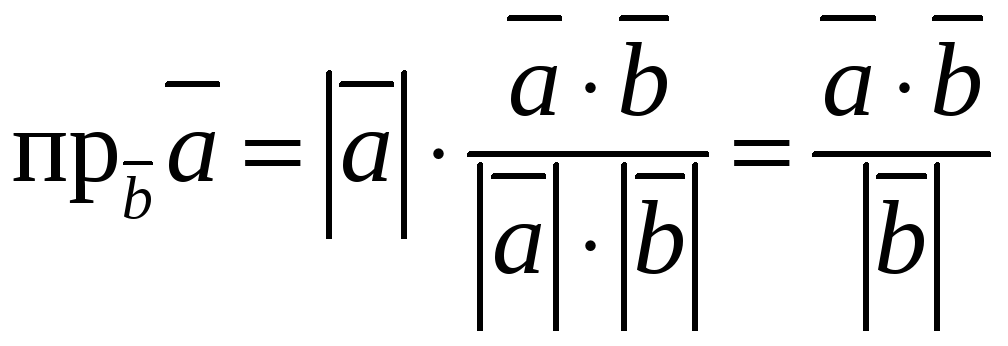Для нахождения проекции вектора на направление вектора находим координаты векторов , , а затем, применяя формулу

,

получаем

.

г) Для нахождения угла определяем векторы , , имеющие общее начало в точке :

,

.

Затем по формуле скалярного произведения

находим

,

.

д) Для того чтобы три вектора

, ,

были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю.

В нашем случае имеем .

Следовательно, векторы компланарны.