- •Методические указания
- •1. Электростатическое поле в вакууме
- •1.1. Основные законы и формулы
- •1.2. Качественные задачи
- •1.3. Основные типы задач и методы их решения
- •1.4.Задачи для самостоятельного решения и контрольных заданий
- •2. Проводники и диэлектрики в электрическом поле
- •2.1. Основные законы и формулы
- •2.2. Качественные задачи
- •2.3. Основные типы задач и методы их решения
- •2.4. Задачи для самостоятельного решения и контрольных заданий
- •3. Электроёмкость. Энергия электрического поля
- •3.1. Основные законы и формулы
- •3.2 Качественные задачи
- •3.3. Основные типы задач и методы их решения
- •3.4. Задачи для самостоятельного решения и контрольных заданий
- •4. Постоянный электрический ток
- •4.1 Основные законы и формулы
- •4.2 Качественные задачи
- •4.3 Основные типы задач и методы их решения
- •4.4 Задачи для самостоятельного решения и контрольных заданий
- •БИблиогрфический список
- •394026 Воронеж, Московский просп., 14
2. Проводники и диэлектрики в электрическом поле
2.1. Основные законы и формулы
1. Поляризованность диэлектрика
![]() ,
,
где
![]() - дипольный
момент
- дипольный
момент
![]() -й
молекулы;
-й
молекулы;![]() -
объем диэлектрика.
-
объем диэлектрика.
2. Связь между поляризованностью диэлектрика и напряженностью электростатического поля
![]() ,
,
где χ - диэлектрическая восприимчивость вещества.
3. Вектор электрического смещения
![]() ;
;
![]() ,
,
где
![]() - диэлектрическая
проницаемость.
- диэлектрическая
проницаемость.
4. Теорема Гаусса для электростатического поля в диэлектрике
![]() ,
,
где
![]() - алгебраическая сумма заключенных
внутри замкнутой поверхности сторонних
электрических зарядов.
- алгебраическая сумма заключенных
внутри замкнутой поверхности сторонних
электрических зарядов.
5. Условия на границе раздела двух диэлектриков
![]() ,
,
![]() .
.
6. Поле в однородном диэлектрике
![]() ,
,
![]() .
.
где
![]() ,
,
![]() -
напряженность и электрическое смещение
внешнего поля.
-
напряженность и электрическое смещение
внешнего поля.
7. Напряженность
электростатического поля у поверхности
проводника
![]() ,
,
где
![]() - поверхностная плотность зарядов.
- поверхностная плотность зарядов.
2.2. Качественные задачи
|
|
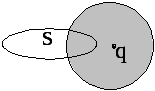
1. Точечный
заряд
|
|
|
2.
Точечный заряд
a)
|
3.
В центре воображаемой сферы находится
точечный заряд. Изменится ли поток
вектора
![]() через эту
поверхность, если:
через эту
поверхность, если:
а) все пространство заполнить однородным и изотропным диэлектриком;
б) заменить сферическую поверхность кубической с центром в заряде?
4. В области, ограниченной заземленной металлической оболочкой, находится заряд. Определить: а) есть ли электрическое поле вне оболочки; б) будет ли действовать электрическая сила на другой заряд, помещенный вблизи наружной поверхности оболочки.
5.
По представленным рисункам определить,
с помощью каких линий (![]() или
или![]() )
изображено
электростатическое поле и как соотносятся
)
изображено
электростатическое поле и как соотносятся
![]() и
и![]() ?
?
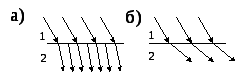
2.3. Основные типы задач и методы их решения
а) Классификация
1. Расчет электростатических полей в диэлектрических средах. Определение напряженности, индукции и потенциала электростатического поля внутри однородного, изотропного диэлектрика.
Метод
решения.
Использование теоремы Гаусса для вектора
![]() и соотношения, связывающего между собой
и соотношения, связывающего между собой![]() и
и
![]() .
Воспользоваться аналогичной теоремой
для поля
.
Воспользоваться аналогичной теоремой
для поля![]() не представляется
возможным, поскольку не известен
связанный заряд.
не представляется
возможным, поскольку не известен
связанный заряд.
2. Нахождение напряженности и индукции поля на границе раздела двух сред.
Метод
решения.
Использование соотношений между
нормальными и тангенциальными
составляющими векторов
![]() и
и
![]() на границе
раздела двух сред.
на границе
раздела двух сред.
б) Примеры решения задач
1.
Точечный заряд
![]() находится в центре шара радиусом
находится в центре шара радиусом![]() из однородного
изотропного диэлектрика проницаемостью
из однородного
изотропного диэлектрика проницаемостью
![]() .
Найти напряженность поля как функцию
расстояния
.
Найти напряженность поля как функцию
расстояния![]() от центра шара. Представить графики
зависимостей
от центра шара. Представить графики
зависимостей
![]() и
и![]() .
.
Решение.
В
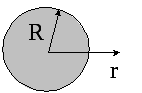
![]() и
и![]() направлены радиально. Поток вектора
направлены радиально. Поток вектора![]() через сферическую поверхность радиусом
через сферическую поверхность радиусом![]()
![]() .
.
По
теореме Гаусса:
![]() ,
откуда
,
откуда
![]() .
.
Так
как
![]() ,
то
,
то
для
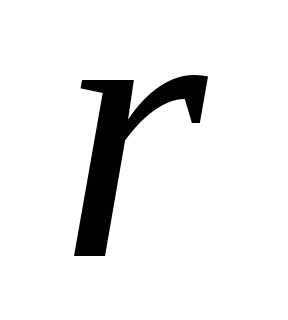 <
<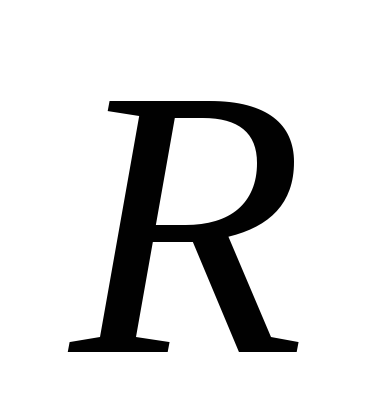 ,
,
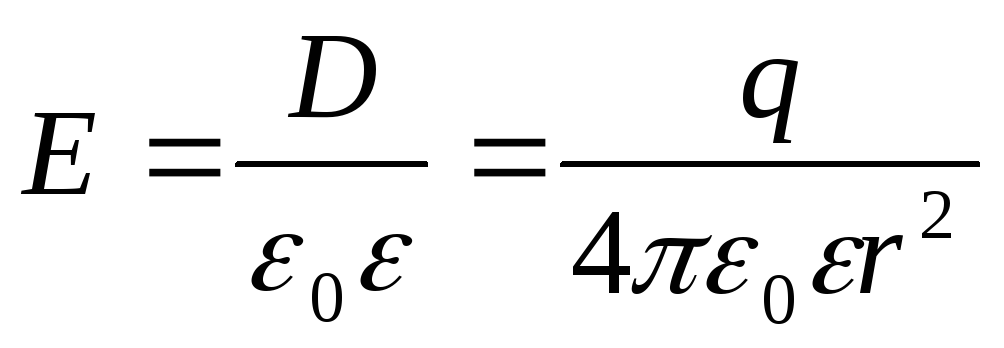 .
.для
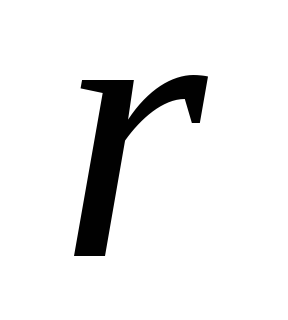 >
>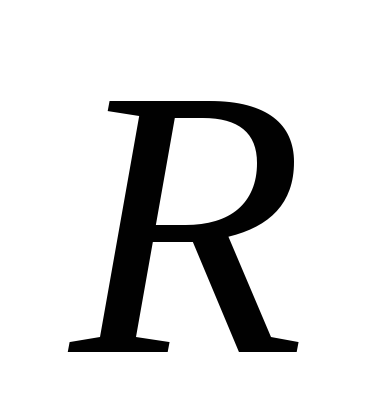 ,
,
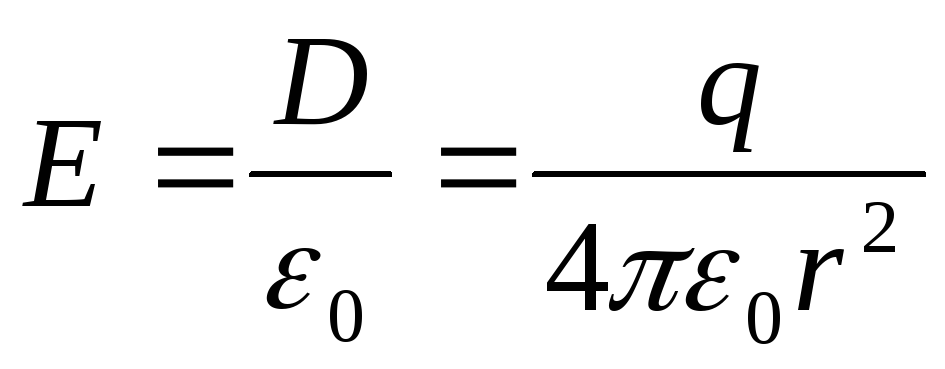 .
.
Г
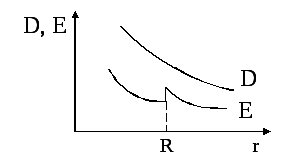
![]() и
и![]() имеют следующий вид:
имеют следующий вид:
2
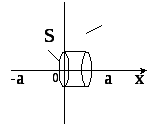
![]() заряжена равномерно сторонним зарядом
с объемной плотностью
заряжена равномерно сторонним зарядом
с объемной плотностью![]() >0.
Толщина пластины 2а. Найти
>0.
Толщина пластины 2а. Найти![]() и
и![]() как функции расстояния
как функции расстояния![]() от середины пластины
(потенциал в сере
от середины пластины
(потенциал в сере дине
пластины положить равным нулю). Определить
поверхностную плотность связанного
заряда.
дине
пластины положить равным нулю). Определить
поверхностную плотность связанного
заряда.
Решение.
Из
соображений симметрии ясно, что в
середине пластины
![]() ,
а во всех остальных точках вектор
,
а во всех остальных точках вектор
![]() перпендикулярен
поверхности пластины. Воспользуемся
теоремой Гаусса для вектора
перпендикулярен
поверхности пластины. Воспользуемся
теоремой Гаусса для вектора
![]() .
В качестве замкнутой поверхности возьмем
прямой цилиндр высотой
.
В качестве замкнутой поверхности возьмем
прямой цилиндр высотой![]() ,
один торец которого совпадает со средней
плоскостью пластины. Пусть площадь
сечения этого цилиндра равна
,
один торец которого совпадает со средней
плоскостью пластины. Пусть площадь
сечения этого цилиндра равна![]() ,
тогда
,
тогда
1)
для
![]() :
:
![]() ,
,![]() ,
,![]() ;
;
2)
для
![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Используя
выражение
![]() ,
получаем
,
получаем
1)
для
![]()
![]() ;
;
![]() и
и![]() ;
;
2)
для
![]()
![]()
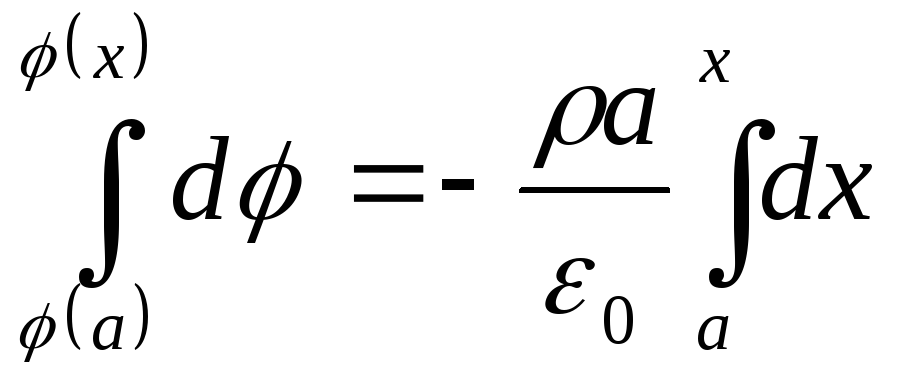 ;
;
![]() .
.
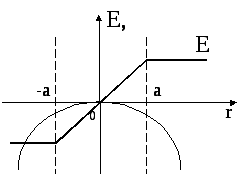
Графики
функции
![]() и
и
![]() представлены
на рисунке.
представлены
на рисунке.
Поверхностную плотность связанного заряда определим из выражения
![]() ’=
’=
![]() /
/![]() >0.
>0.
Таким
образом, если сторонний заряд
![]() > 0, то на обеих поверхностях пластины
будет также положительный связанный
заряд.
> 0, то на обеих поверхностях пластины
будет также положительный связанный
заряд.
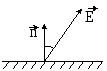
3.
Вблизи границы раздела вакуум - диэлектрик
напряженность электрического поля в
вакууме равна
![]() ,
причем вектор
,
причем вектор![]() составляет
угол
составляет
угол
![]() с нормалью к
поверхности раздела. Проницаемость
диэлектрика
с нормалью к
поверхности раздела. Проницаемость
диэлектрика
![]() .
Найти отношение
.
Найти отношение![]() ,
где
,
где
![]() напряженность
поля внутри диэлектрика.
напряженность
поля внутри диэлектрика.
Решение.
Напряженность поля внутри диэлектрика
![]() .
.
Воспользовавшись условиями на границе раздела диэлектрика, найдем
![]() ;
;
![]() ,откуда
,откуда
![]() <
1, т.е
<
1, т.е
![]() .
.