Техническая термодинамика

Объемная теплоемкость смеси газов

i 1

где ri и ci| - доли компонентов по объему и объемные теплоемкости отдельных

компонентов.

Парциальное давление отдельного компонента

Задачи Задача 2.1. Определить массовый состав сухого воздуха, его удельную

газовую постоянную, кажущуюся относительную молекулярную массу и плотность при абсолютном давлении 110 кПа и температуре 20% кислорода и 79% азота.

Решение. Между массовыми и объемными составами газовой смеси существует зависимость qi = riМi/Мcм

Кажущуюся молекулярную массу газовой смеси можно определить по формуле 2.11

Тогда

qN2 rN2 M N2 M см =0,79 ·28/28,84=0,767; qO2 1 qN2 =1-0,767=0,233.

Удельная газовая постоянная смеси определяется по формуле 2.14

Rсм=8314,3/Мсм=8314,3/28,84=288,3 кДж/(кг∙K)

Плотность газовой смеси определяем из формулы

Задача 2.2. Смесь двух объемов водорода и одного объема кислорода называют гремучим газом. Определить кажущуюся молекулярную массу, газовую постоянную и массовый состав гремучего газа.

Задача 2.3. Смесь газов состоит из 1,0 м3 генераторного газа и 1,5 м3 воздуха, взятых при нормальных физических условиях. Определить газовую постоянную смеси газов и парциальные давления составляющих смеси. Плотность генераторного газа ρ2 принять равной 1,2 кг/м3.

Задача 2.4. В цилиндр газового двигателя засасывается газовая смесь, состоящая из 20 массовых долей воздуха и 1 доли коксового газа.

Определить плотность и удельный объём смеси при нормальных условиях, а также парциальное давление воздуха в смеси. Плотность коксового газа при нормальных условиях 0,515 кг/м3?.

Задача 2.5. Анализ продуктов сгорания, произведенный с помощью газоанализатора показал их следующий объемный состав: СО2=12,2%; О2=7,1%; СО=0,4%; N2=80,3%. Определить массовый состав входящих в смесь газов.

11

Задача 2.6. Определить объем смеси газов при абсолютном давлении 100 кПа и температуре 900С, образовавшийся при смешивании 100 кг топочных газов с 50 кг воздуха. Массовый состав топочных газов 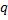со=0,18; qНо=0,08;

qо=0,02, и qN=0,72.

Задача 2.7. Определить среднюю мольную, объемную и весовую теплоемкости в процессах постоянного давления и постоянного объема в интервале температур от 0 до 1300°C для смеси газов, имеющий следующий объемный

пература t0 20 C.

3 ТЕПЛОЕМКОСТЬ ГАЗОВ

Теплоемкостью газа называют количество теплоты, необходимое для повышения его температуры на 1 К. Теплота, затраченная на повышение температуры единицы количества газа на 1 К называется удельной теплоемкостью. Принято удельную теплоемкость называть просто теплоемкостью.

В зависимости от выбранной количественной единицы различают тепло-

емкости: мольную Сm-кДж/(кмоль·К), массовую С – кДж/(кгК), и объемную С’

– кДж/(м3К).

Так как в 1 м3 газа могут содержаться, в зависимости от параметров его состояния, разные количества газа, принято относить 1 м3 газа к нормальным условиям (Р0= 101325 Па, Т0=273,15 К).

Между теплоемкостями существует следующее соотношение

где ρ0 – плотность газа при нормальных условиях.

Теплоемкость газа зависит от его температуры. По этому признаку отличают истинную и среднюю теплоемкость.

Если q – удельное количество теплоты, сообщаемой единице количества

Представляет собой среднюю теплоемкость в пределах от t2 до t1.

Предел этого отношения, когда разность температур стремиться к нулю, называют истинной теплоемкостью. Аналитически последняя определяется как

Теплоемкость зависит от вида процесса сообщаемая газу теплоты.

12

Количество теплоты, которое необходимо затратить для нагревания или охлаждения рабочих тел определяются из соотношений а) для 1 кг

В зависимости от условий, при которых протекают нагревание (охлаждение) газа (V- const , p- const ) в формулах 3.6...З.10 ставятся соответствующие значения теплоемкости.

Теплоемкость смеси идеальных газов

Задачи Задача 3.1. Вычислить количество теплоты необходимой на нагревание

при постоянном давлении р=100 кПа ,60 м3 воздуха от 10° до 500°С. Задачу решить в трех вариантах:

а) считая зависимость теплоемкости от температуры криволинейной; б) пользуясь формулой линейной зависимости средней теплоемкости

воздуха от температуры; в) полагая, что теплоемкость не зависит от температуры.

Решение. Количество теплоты, необходимое на нагревание воздуха, исходя из криволинейной зависимости теплоемкости от температуры определяем по следующей формуле, полученной на основании уравнений (3.7)и(3.8)

Если использовать при решении задачи объемные теплоемкости, то нужно найти объем воздуха при нормальных условиях (Р0=101325 Па и Т0=273,15 К). Можно определить массу воздуха и применить массовые теплоемкости.

Определяем массу воздуха по уравнению

Из приложения 1 выбираем средние изобарные массовые теплоемкости от

0 до 10 и от 0 до 500°С.

14

Qp 10500 7,39(1,0925 500 1,0067 10) 3962 кДж;

В случае линейной зависимости теплоемкости от температуры формула для определения количества теплоты будет выглядеть

а при постоянной теплоемкости

Во второй случае использовали уравнения (3.6), (3.8) и приложение 2, а в третьем- (3.1), (3.8) и таблицу 3.1.

Задача 3.2. В котел-утилизатор поступают дымовые газы с температурой 1200°С следующего объемного состава: СО2=12%; О2=6%,N=74%; пары воды H2O=8% при давлении 200 кПа. Определить количество подаваемой теплоты нагреваемой воде, если температура газов при выходе из котла 200°С, к.п.д котла – 70% и расход дымовых газов 10 м 3/ч

Решение. Определяем количество теплоты, отведенной от дымовых газов по уравнению

где Vo - объём газовой смеси при нормальных условиях;

ri - объемные доли отдельных компонентов дымовых газов.

Из уравнения состояния для m кг идеального газа необходим объем дымовых газов при нормальных условиях

Среднюю теплоемкость газов, входящих в состав дымовых газов берем из приложения 1

2.2638 0.12 1.5005 0.06 1.4202 0.74 1.7769 0.08 1200 2779.23 кДж.

Задача 3.3. Вычислить количество теплоты, удаляемое из птичника с отсасываемым воздухом, если температура внутри помещения 16,а наружного - 0°С. Объемная подача вентилятора 20 тыс. стандартных м3/ч.

Задача 3.4. В конденсатор холодильной установки с водяным охлаждением поступает газообразный аммиак давлением р =1,05 MПa и температурной 122°С, охлаждается до t=27°C. Объемный расход аммиака V t=0,04 м3/с. Вода в конденсаторе нагревается на 60С. Определить количество отведенной теплоты

15

и массовый расход воды на охлаждение конденсатора. Зависимость теплоемкости от температуры не учитывать.

Задача 3.5. В баллоне объемом 60л находится кислород при давлении 5 МПа и температуре 20°С. Какое количество тепла подведено, к кислороду, если его температура повысилась до 150°С. Какое давление установится при этом в сосуде? Зависимость теплоемкости от температуры. принять криволинейной.

Задача 3.6. В воздухоподогревателе котельного агрегата дутьевой воздух нагревается дымовыми газами, от 20 до 200°С. При этом температура, дымовых газов понижается от 350 до 160°С. Объемный состав дымовых газов: СО2=12%; О2=6%,N=74%, H2O=8%. Определить соотношение расходов воздуха и дымовых газов. Зависимость теплоемкости газов и воздух от температуры считать прямолинейной.

Задача 3.7. Определить среднюю мольную, объемную и весовую теплоемкости в процессах постоянного давления и постоянного объема в интервале температур от 0 до 1300°C для смеси газов, имеющий следующий объемный состав: 8% СО2 ; 2% СО и 85% N 2 ; 5% H 2 .

4 ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ ГАЗОВ

Изменение состояния тела при взаимодействии его с окружающей средой называется термодинамическим процессом. В общем случае термодинамическом процессе могут изменяться все параметры состояния. В технической термодинамике рассматриваются следующие основные процессы:

изохорный - при постоянном объеме (V=const); изобарный - при постоянном давлении (р =const); изотермический - при постоянной температуре (Т=const); адиабатный - без теплообмена (q=const);

политропный- ( pvn =const); где n - показатель политропы.

Изменение внутренней энергии в термодинамических процессах с идеальным газом

Работа изменения объема 1кг газа

16

Зависимость между основными параметрами состояния, работа изменения объема газа определяется по формулам, аналогично 4.17… 4.21, но вместо показателя адиабаты применяется показатель политропы.

Количество теплоты политропного процесса

Задачи

Задача 4.1. В закрытом помещении, объемом V=150 м3 находится воздух при давлении Р=100 кПа и температуре t1=5 °С. Через некоторое время, температура воздуха повышается до 30°С. Определить какое количество теплоты сообщено воздуху, изменение внутренней энергии, и энтальпии воздуха, его конечное давление.

Решение. Нагревание воздуха протекает при постоянном, объеме, т.е. процесс изохорный. Из уравнения 4.3. Определяем конечное давление

В связи с тем, что температура повышается незначительно, теплоемкость воздуха можно считать постоянной .

Задача 4.2. При изобарном расширении углекислого газа температура его уменьшилась от 300 до 50°С. Определить доли теплоты, затраченной на изменение внутренней энергий и на совершение работы.

18

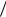
Решение: В изобарном процессе подведенная теплота расходуется на изменение внутренней энергии и на совершение работы, и уравнение первого закона термодинамики принимает вид

q U w.

Чтобы определить доли теплоты на изменение внутренней энергии и на совершение работы разделим данное уравнение на q

довательно, в изобарном процессе 22,5% теплоты превращается в работу, а 77,5 %расходуется на изменение внутренней энергии.

Задача 4.3. В охлаждаемом компрессоре изотермно сжимается V0=60 м3/ч воздуха до давления 0.6 МПа, определить затраченную мощность на сжатие и часовой расход охлаждающей воды mt компрессора, если вода нагревается при этом на 10°С.

Решение. Определяем мощность, затраченной на сжатие 60 м3/ воздух. Для изотермного сжатия

В изотермическом процессе вся затраченная работа на сжатие превращается в теплоту, которая отводится охлаждающей водой

Задача 4.4. При нормальной, работе топливной аппаратуры двигателя температура смеси газов в цилиндре достигает 1900 К. После, сгорания следует политропическое расширение с показателем 1.3. Объем газов при этом до открытия выпускного клапана увеличивается в 12 раз. Насколько повышается температура газов, в момент открытия выпускного клапана, если в результате ухудшения работы топливной аппаратуры при расширении топливо догорает, благодаря чему значение показателя политропы расширения становится равным 1.2. Состояние газов до расширения в обоих случаях считать одинаковым.

Решение. Из соотношения параметров политропного процесса с показателями политропы n=1,3 и n=1,2 определяем конечные температуры в конце расширения

По условию задачи v1 v2 12 .Тогда

19

T2 T1 v1 n 1

v2

Если расширение происходит с показателем политропы n=1.3, то

ет с давлением Р1=100 кПа, и сжимает его до давления Р2=0.7 МПа по политропе с показателем n=1,25. Вычислить, на сколько изменится работа сжатия , если сжатие будет происходить по изотерме. Температура окружающей среды 200С.

Задача 4.6. В процессе политропного расширения воздуху сообщается 80 кДж теплоты. Определить изменение внутренней энергии воздуха и производственную работу, если объем воздуха увеличился в 10 раз, а давление его уменьшилось в 8 раз.

Задача 4.7. 2 м3 кислорода расширяется политропно от р1=0,5 МПа и t1=400C до р2=0,15 МПа. Объем занимаемый при этом воздухом, становится равным 10 м3 . Определить показатель политропы, конечную температуру, ра-

р2=0,2МПа. Определить конечные температуру, удельный объем и работу расширения.

Задача 4.9. Кислороду в количестве 0,5 м3 при р1 =0,8 МПа и t=40°С. сообщается изотермически 65,45 кДж теплоты. Определить конечные давление и объем.

Задача 4.9. Определить тепловой поток Ф, отдаваемое уходящими газами котельной мясокомбината водяному экономайзеру для подогрева питательной воды если температура дымовых газов при входе в экономайзер 320 С, на выходе 200 С, средняя объемная теплоемкость дымовых газов Сд.г.=1,415 кДж/(м к) расчетный расход топлива для одного котла Вр=0,25 кг/с. Теоретический объем воздуха V=5,17 м3/кг, расход уходящих газов перед экономайзером 8,4 м3/с, за экономайзером 6,7 м3.

5 ВОДЯНОЙ ПАР. ДИАГРАММА hS ВОДЯНОГО ПАРА. ИССЛЕДОВАНИЕ ПАРОВЫХ ПРОЦЕССОВ ПО ДИАГРАММЕ hS

Вода и. водяной пар широко применяются в энергетике, в отоплении, вентиляции, горячем водоснабжении.

Водяной пар - реальный газ. Он может быть влажным, сухим насыщенным и перегретым. Уравнения состояния реальных газов сложны, поэтому в теплотехнических расчетах предпочитают использовать таблицы и диаграммы.

20