4 Определение приведённого момента производственного (полезного) сопротивления и его работы

▌^* Для унификации дальнейшего текста величина производственного

cопротивления обозначается символом «X».В зависимости от задания

следует писать М_п.с. или Р_п.с.. ^* ▌

Из всех активных сил, действующих на машину, учтем только момент двигателя и производственное сопротивление. Влиянием сил трения, сил сопротивления среды и сил тяжести пренебрегаем.

Величина производственного сопротивления P_пс линейно зависит от угла поворота кривошипа. В начале рабочего хода звена 3 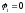,; в конце рабочего хода присопротивление равняется заданному максимальному значению=….. Тогда в произвольном положении

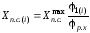. (15)

Точное значение угла поворота кривошипа 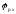за время рабочего хода звена 3 определяется на компьютере при кинематическом расчёте рычажного механизма. Это позволяет получить массив значений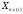на границах каждогоi-того шага 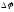при изменении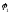от нуля до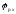, а также массив значений приведенного момента сопротивления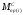, который определяется из условия равенства мощносте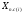йи: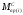

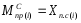· ▌^* дописать.^* ▌ (16)

Значения приведенного момента инерции 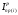и приведенного момента 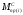сопротивленияизвлекаются из памяти компьютера на каждом шаге вычисления угловой скорости кривошипа по формуле (11). Одновременно определяется модуль приращения работы полезного сопротивления

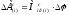, (17)

За время цикла полезное сопротивление совершает работу на угле поворота кривошипа 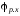.Тогда модуль работы за цикл будет равен сумме

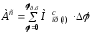. (18)

5 Определение движущего приведенного момента

НА КАЖДОМ ПРОМЕЖУТОЧНОМ ШАГЕ ВЫЧИСЛЕНИЙ

Приведенный движущий момент в начале i-того шага найдем с помощью механической характеристики двигателя, рисунок 3, приведенной к валу кривошипа: по оси абсцисс – угловая скорость кривошипа, по оси ординат – приведенный движущий момент, связанный с моментом двигателя равенством мощностей. Момент 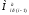и скорость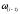были вычислены на предыдущем шаге расчетов.

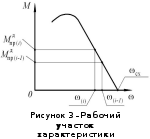Из подобия треугольников на рисунке 3 запишем

.

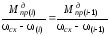Отсюда находим значение момента на i – ом шаге расчетов:

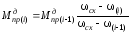. (19)

Скорость кривошипа, соответствующая синхронной частоте вращения, определяется по формуле

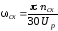, (20)

где U_р – модуль общего передаточного отношения редуктора, формула (6).

Таким образом, все величины, необходимые для вычисления угловой скорости 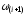по формуле (11) определены. Не заданы только скорость и приведенный момент для расчётов на первом шаге: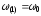,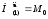. Их точные значения заранее неизвестны. ▌^* Номер шага расчётов соответствует номеру интервала 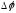изменения угла. На первом интервале происходит поворот из нулевого в первое положение. 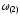Соответственно, на первом шаге расчётов вычисляется величина , принятая постоянной на втором интервале изменения угла.^* ▌