3. По результатам многократного измерения детали определить предельную случайную погрешность измерения. Исходные данные к задаче в табл. 3.

Условие: измерение производиться относительным методом с помощью индикатора с ценой деления 0,01 мм с применением концевой меры длины 3-го класса из стали Х в помещении с температурой +15 ^оС ÷ +25 ^оС. Погрешность концевой меры длины – 2,5 мкм, погрешность индикатора – 7 мкм; погрешность отсчета – 2 мкм. Вал изготовлен из алюминия. Температура вала и средств измерения выровнена с температурой помещения.

Таблица 3

Исходные данные к задаче 3

Варианты
1	2	3	4	5
Результаты измерения деталей, мм
35,017	18,065	16,01	24,94	12,000
35,015	18,068	16,03	24,93	12,002
35,016	18,070	16,02	24,92	11,999
35,019	18,067	16,04	24,98	11,998
35,017	18,069	16,05	24,96	12,001
35,018	18,066	16,01	24,95	11,998
35,016	18,072	16,03	24,97	12,003
35,017	18,071	16,05	24,99	12,001
35,018	18,069	16,02	24,93	12,003
35,014	18,067	16,03	24,94	12,002

4. Определить предельную случайную погрешность измерения линейных размеров в случаях применения измерительных средств и условий, приведенных в табл. 4 (температура измеряемых деталей и средств измерений выравнена с температурой окружающей среды).

Таблица 4

Исходные данные к задаче 4

Варианты	1	2	3	4	5
Измеряемый размер детали, мм	120	20	50	150	80
Материал детали	Бронза	Сталь	Титан	Чугун	Твердый сплав
Колебание температуры в помещении, 0С	18-22	17-23	19-21	16-24	18-22
Наименование и погрешность средства измерения, мкм	2МИГ 3	ИГП 0,5	Оптикатор, 0,5	ГИРБ 3	ОВО-1 0,2
Погрешность отсчета, мкм	0,2	0,2	0,1	0,2	0,15
Материал концевых мер длины	Сталь Х	Твердый сплав ВК-6М	Сталь Х	Сталь Х	Сталь Х
Погрешность блока концевых мер дины (при температуре 200С)	2,8	1,1	0,8	3	1,2

Контрольные вопросы для самопроверки

1. Какие погрешности бывают? Перечислите их.

2. Напишите формулу для определения среднего квадратического отклонения.

Литература

Белкин И.М. Средства линейно-угловых измерений: Справ. – М.: Машиностроение, 1987. – 368 с.

Зинин Б.С., Ройтенберг Б.Н. Сборник задач по допускам и техническим измерениям: Учеб. пособие. – М.: Машиностроение, 1988. – 160 с.

ПРАКТИЧЕСКАЯ РАБОТА № 2

Проверка нормальности закона распределения вероятности результата измерений

Цель занятия: проверить гипотезу о нормальности распределения результатов наблюдений.

Оснащение:

• методические указания по выполнению практической работы;

• справочные данные;

• микрокалькулятор.

Работа рассчитана на 5 академических часов.

ОСНОВНЫЕ ПОЛОЖЕНИЯ

Сходность результатов наблюдений можно оценить наиболее полно, если их распределение является нормальным. Поэтому исключительно важную роль играет проверка нормальности распределения.

Поскольку ошибки искажают эмпирический закон распределения вероятности результата измерения, поскольку проверка предположения о его нормальности производится после исключения ошибок.

При большом числе результатов наблюдений (n > 40) данная задача решается в следующем порядке:

Весь диапазон полученных результатов наблюдений X_max –X_min разделяют на r интервалов шириной ΔX_i (i = 1, 2,…, r) и подсчитывают частоты m_i, равные числу результатов, лежащих в каждом i-м интервале, т.е. меньших или равных его правой и больших левой границы.

Отношение ,

где n – общее число наблюдений, называют частостями и представляют собой статистические оценки вероятностей попадания результатов наблюдений в i–й интервал.

Распределение частостей по интервалу образует статистическое распределение результатов наблюдений.

Если теперь разделить частость на длину интервала, то получим величины , (1)

являющиеся оценками средней плотности распределения в интервале ΔX_i.

Отложим вдоль оси результатов наблюдений интервалы ΔX_i (рис. 1) в порядке возрастания индекса i и на каждом интервале построим прямоугольник с высотой p*_i. Полученный график называется гистограммой статистического распределения. Площадь всех прямоугольников равна единице.

Р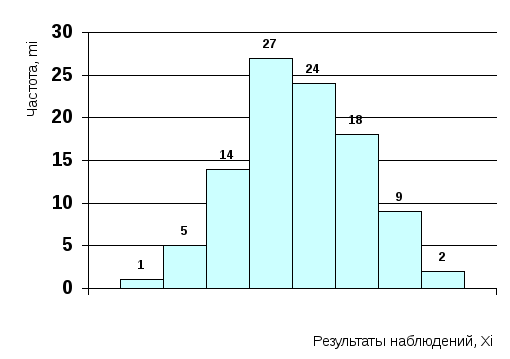ис. 1. Гистограмма статистического распределения

При построении гистограмм рекомендуется пользоваться следующими правилами:

1. Число r интервалов выбирается в зависимости от числа наблюдений согласно рекомендациям ВНИИМ:

Число измерений	Рекомендуемое число интервалов
40 –100 100 – 500 500 – 1000 1000 – 10000	7– 9 8 – 12 10 – 16 12 – 22

2. Длины интервалов ∆X_i удобнее выбирать одинаковыми. Однако если распределение крайне неравномерно, то в области максимальной концентрации результатов наблюдений следует выбирать более узкие интервалы.

3. Масштабы по осям гистограммы должны быть такими, чтобы отношение ее высоты к основанию составляло, примерно, 5:8.

После построения гистограммы подбирают теоретическую плавную кривую распределения, которая, выражая все существенные черты статистического распределения, сглаживает все случайности, связанные с недостаточным объемом экспериментальных данных.

Принципиальный вид теоретической кривой выбирают заранее, проанализировав метод измерения. Тогда определение аналитического вида кривой распределения сводится к выбору таких значений его параметров, при которых достигается наибольшее соотношение между теоретическим и статистическим распределением.

Одним из методов решения этой задачи является метод моментов. При использовании этого метода параметрам теоретического распределения придают такие значения, при которых несколько важнейших моментов совпадают с их статистическими оценками.

На основании построенной гистограммы, полученной при обработке опытных данных, строится гипотеза, состоящая в том, что результаты наблюдений подчиняются распределению F_x (x) с плотностью p_x (x).

Для принятия или опровержения этой гипотезы выбирается некоторая величина , представляющая собой меру расхождения теоретического и статистического распределения. В качестве меры расхождения можно принять сумму квадратов разностей частостей теоретических вероятностей попадания результатов наблюдений в каждый интервал, взятых с некоторыми коэффициентами:

(2)

где c_i – коэффициенты, называемые весами разрядов; P_i – теоретические вероятности, определяемые как 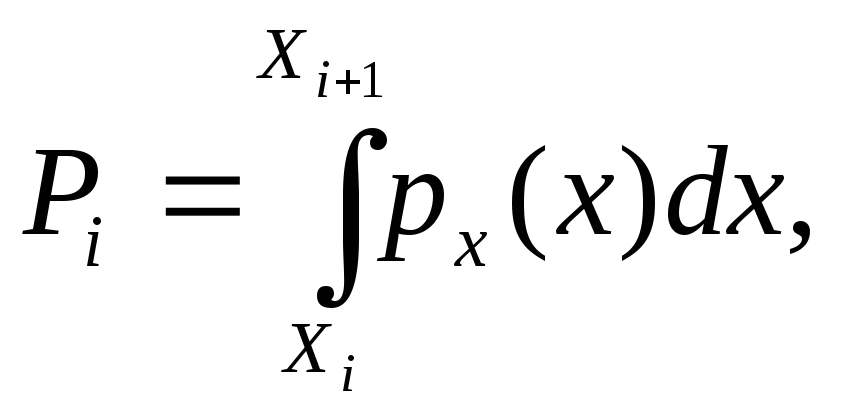(3)

где р_х (х) - предполагаемая плотность распределения.

Мера расхождения U является случайной величиной и, как показал К. Пирсон, независимо от исходного распределения подчиняется – распределению

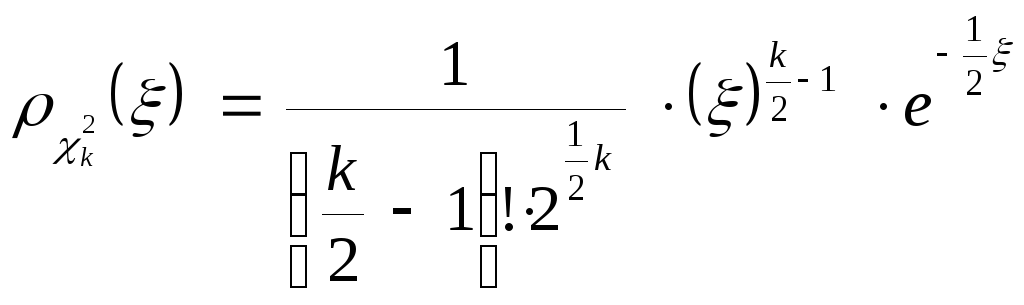, (4)

где k = n – 1 – число степеней свободы распределения, на единицу меньшее числа измерений, на основании которого определяется оценка дисперсии. Если все частотыm_i. ≥ 5, число измерений стремиться к , а веса c_i выбирается равным . Число степеней свободы распределения, гдеr – число разрядов гистограммы статистического распределения, а s – число независимых связей, наложенных на частности . Если проверяется гипотеза о нормальности распределения, то к числу этих связей относится равенство среднего арифметического и точечной оценки дисперсии соответственно математическому ожиданию и дисперсии нормального распределения. Кроме того, всегда требуется, чтобы сумма частостей по всем интервалам была равна единице. Поэтому в данном случае,s = 3.

Мера расхождения U (по К. Пирсону) обозначается через :

(5)

При заданной доверительной вероятности     q, можно найти тот доверительный интервал значений, в которой мера расхождения может попасть по чисто случайным причинам.

Если вычисленная по опытным данным мера расхождения окажется в указанном интервале, то гипотеза не противоречит опытным данным. Если жевыходит за границы доверительного интервала, то гипотеза отвергается как противоречащая опытным данным.

Описанная процедура проверки гипотезы говорит о том, что данное статистическое распределение является распределением с плотностью p_x(x), называется критерием согласия. Критерий согласия, построенный на предельном переходе приn → ∞, рекомендуется применять, если общее число наблюдений более 40.