
-
Транспортная задача
Задача 4. В таблице
даны запасы (в тоннах) однородного
сыпучего груза у поставщиков (![]() ,
,
![]() ,
,
![]() ),
спрос на него потребителей (
),
спрос на него потребителей (![]() ,
,
![]() ,
,
![]() ,
,
![]() ),
а также матрица тарифов перевозок,
элементы которой
),
а также матрица тарифов перевозок,
элементы которой
![]() равны стоимостям перевозок одной тонны
груза из пункта отправления
равны стоимостям перевозок одной тонны
груза из пункта отправления
![]() в пункт назначения
в пункт назначения
![]() (в условных денежных единицах)
(в условных денежных единицах)
|
|
|
|
|
|
|
||||||||
|
450 |
250 |
100 |
100 |
|
|||||||||
|
|
200 |
|
6 |
|
4 |
|
4 |
|
5 |
||||
|
|
|
|
|
||||||||||
|
|
300 |
|
6 |
|
9 |
|
5 |
|
8 |
||||
|
|
|
|
|
||||||||||
|
|
400 |
|
8 |
|
2 |
|
10 |
|
6 |
||||
|
|
|
|
|
||||||||||
Требуется:
1) Составить математическую модель транспортной задачи, заданной таблицей.
2) Найти оптимальный план перевозок груза, минимизирующий общую стоимость всех перевозок.
Решение:
1) Для составления математической модели данной транспортной задачи сначала введем переменные:
![]() - количество единиц
(тонн) груза, планируемое к перевозке
из пункта отправления
- количество единиц
(тонн) груза, планируемое к перевозке
из пункта отправления
![]() в пункт назначения
в пункт назначения
![]() (
(![]() ).
).
Затем запишем выражение целевой функции, имеющей смысл суммарной стоимости всех перевозок:
![]()
![]() .
.
Далее составим систему ограничений на переменные, исходя из следующих требований:
- все запасы груза должны быть вывезены;
- все потребности в грузе должны быть удовлетворены. Получаем следующую систему уравнений:


По смыслу задачи все переменные должны быть неотрицательными:
![]() (
(![]() )
)
Таким образом, приходим к следующей математической формулировке данной транспортной задачи:
Найти такие значения
переменных
![]() ,
которые удовлетворяют составленной
выше системе линейных уравнений и
неравенств и доставляют наименьшее
значение линейной целевой функции
,
которые удовлетворяют составленной
выше системе линейных уравнений и
неравенств и доставляют наименьшее
значение линейной целевой функции
![]() .
.
Задача имеет решение, так как выполнено условие баланса: суммарные запасы груза равны суммарным потребностям.
2) Основными этапами решения поставленной транспортной задачи являются следующие:
- определение начального опорного плана;
- проверка полученного начального опорного плана на оптимальность;
- построение последовательных приближений к оптимальному решению (в случае, если начальный опорный план не является оптимальным).
Для нахождения начального опорного плана применим метод Фогеля. Приведем алгоритм метода Фогеля, следуя работе [4].
"По каждой строке и по каждому столбцу начальной транспортной таблицы определяют разность между двумя наименьшими тарифами и записывают ее соответственно справа и снизу от транспортной таблицы. Из этих разностей выбирают наибольшую, и отмечают ее, заключая в квадрат.
В строке или
столбце, где имеется наибольшая разность,
находят клетку
![]() с наименьшим тарифом и загружают ее
значением
с наименьшим тарифом и загружают ее
значением
![]() .
В строке или столбце с нулевым остатком
груза подчеркивают все незанятые клетки.
.
В строке или столбце с нулевым остатком
груза подчеркивают все незанятые клетки.
Далее описанный процесс повторяют, при этом учитывают только оставшиеся запасы и потребности (заявки). Занятые и прочеркнутые клетки не учитываются при последующих шагах".
Обычно начальный опорный план, полученный методом Фогеля. Будет оптимальным, или близким к оптимальному.
Используя описанный алгоритм, получим следующий начальный опорный план:
|
|
|
|
|
|
||||||
|
450 |
250 |
100 |
100 |
|||||||
|
|
200 |
100 |
6 |
- |
4 |
100 |
4 |
- |
5 |
|
|
|
|
|
|
|||||||
|
|
300 |
300 |
6 |
- |
9 |
- |
5 |
- |
8 |
|
|
|
|
|
|
|||||||
|
|
400 |
50 |
8 |
250 |
2 |
- |
10 |
100 |
6 |
|
|
|
|
|
|
|||||||
***
В результате реализации метода Фогеля все переменные оказываются разбитыми на 2 группы:
- базисные переменные
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
которые соответствуют ненулевым
(загруженным) клеткам;
,
которые соответствуют ненулевым
(загруженным) клеткам;
- свободные
переменные
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
которые соответствуют нулевым
(прочеркнутым) клеткам.
,
которые соответствуют нулевым
(прочеркнутым) клеткам.
Проверим полученный методом Фогеля начальный опорный план на оптимальность. Для этого применим метод потенциалов, краткое изложение которого содержится, например, в работе [5].
Введем так называемые
потенциалы
![]() пунктов отправления
пунктов отправления
![]() (
(![]() )
и потенциалы
)
и потенциалы
![]() пунктов назначения
пунктов назначения
![]() (
(![]() ).
Потенциалы найдем, решая систему линейных
уравнений
).
Потенциалы найдем, решая систему линейных
уравнений
![]() ,
,
где индексы
![]() и
и
![]() соответствуют группе базисных переменных
соответствуют группе базисных переменных
![]() .
.
В данном случае система уравнений для потенциалов имеет вид:
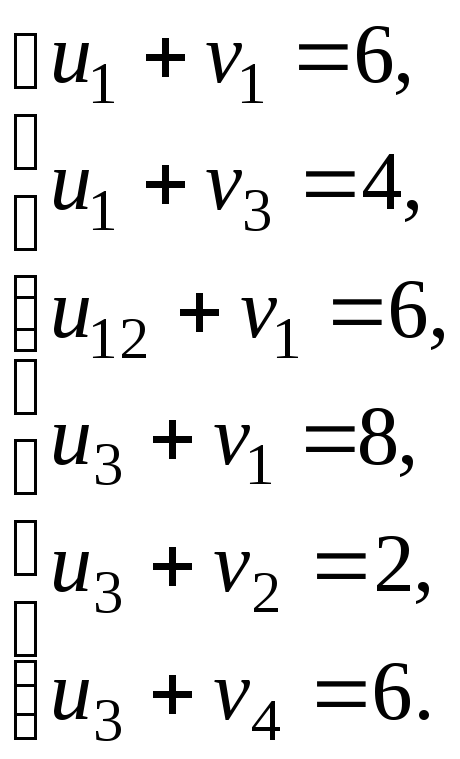
Составленная
система содержит 6 уравнений и 7
неизвестных. Ранг системы равен
![]() .
Следовательно, одна из неизвестных
является свободной. Выберем в качестве
этой переменной
.
Следовательно, одна из неизвестных
является свободной. Выберем в качестве
этой переменной
![]() и примем ее равной нулю:
и примем ее равной нулю:
![]() .
.
Последовательно решая систему, найдем потенциалы всех поставщиков и потребителей:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Далее найдем так
называемые косвенные стоимости
![]() в соответствии с формулой
в соответствии с формулой
![]() ,
,
где индексы
![]() и
и
![]() соответствуют группе свободных переменных
соответствуют группе свободных переменных
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Затем вычисляем
разности стоимостей
![]() (оценки свободных клеток) по формуле
(оценки свободных клеток) по формуле
![]() .
.
Получим следующие значения оценок6
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() .
.
Так как все оценки свободных клеток являются неотрицательными, то начальный опорный план, полученный методом Фогеля, является оптимальным.
Таким образом, искомый оптимальный план перевозок выражается равенствами
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Наименьшая суммарная стоимость всех перевозок, соответствующая найденному оптимальному плану, равна
![]()
![]() (усл. ден. ед.)
(усл. ден. ед.)
5. Условный экстремум. Метод Лагранжа
Задача 5.
На развитие двух
предприятий, входящих в производственное
объединение, выделено2 млн.долл. Если
первому предприятию выделить
![]() млн.долл, то прибыль, полученная от этого
предприятия, будет равна
млн.долл, то прибыль, полученная от этого
предприятия, будет равна
![]() млн.долл; если
млн.долл; если
![]() млн.долл. выделить ворому предприятию,
по прибыль от него будет равна
млн.долл. выделить ворому предприятию,
по прибыль от него будет равна
![]() млн.долл.
млн.долл.
Как следует распределить денежные средства между предприятиями, чтобы суммарная прибыль была максимальной?
Решить задачу методом множителей Лагранжа.
Решение.
Составим математическую модель данной задачи. Для этого сначала введем переменные:
![]() (млн.долл.) –
количество денежных средств, выделяемых
первому предприятию;
(млн.долл.) –
количество денежных средств, выделяемых
первому предприятию;
![]() (млн.долл.) –
количество денежных средств, выделяемых
второму предприятию.
(млн.долл.) –
количество денежных средств, выделяемых
второму предприятию.
Затем запишем выражение целевой функции, имеющей смысл суммарной прибыли производственного объединения:
![]() .
.
Далее составим
уравнение связи:
![]() и представим его в стандартной форме
и представим его в стандартной форме
![]() .
.
В результате получаем задачу условного максимума функции двух переменных при ограничении типа равенства. Для решения этой задачи применим метод Лагранжа ([4], [5]).
Составим функцию Лагранжа
![]() ,
,
где
![]() - числовой параметр, называемый множитель
Лагранжа.
- числовой параметр, называемый множитель
Лагранжа.
Суть метода Лагранжа
состоит в том, что задача нахождения
условного экстремума сводится к
исследованию на обычный (безусловный)
экстремум функции
![]() трех переменных.
трех переменных.
Сначала найдем точки, подозрительные на условный экстремум (стационарные точки функции Лагранжа). Для этого находим частные производные первого порядка от функции Лагранжа, приравниваем их к нулю и решаем полученную систему уравнений:
![]() ,
,
![]() ,
,
![]() ;
;

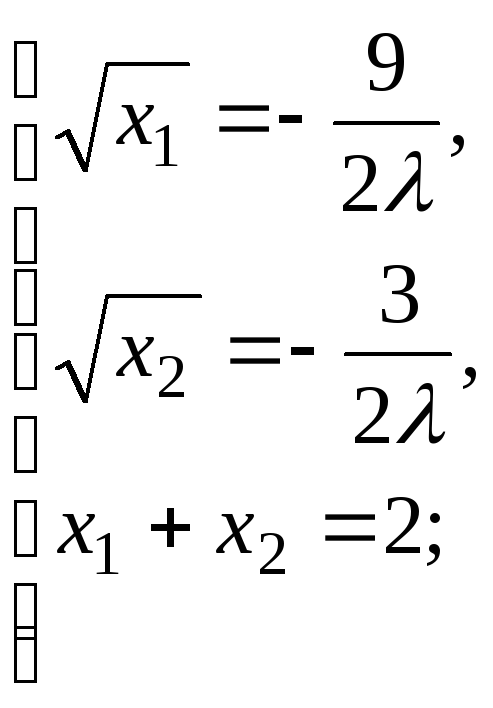

![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Корень
![]() является посторонним; поэтому
является посторонним; поэтому
![]() ,
,
![]() ,
,
![]() .
.
Получаем единственную
стационарную точку функции Лагранжа
![]() .
.
Проверка полученной стационарной точки на выполнение достаточных условий условного экстремума производится с помощью дискриминанта функции Лагранжа

Находим:
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
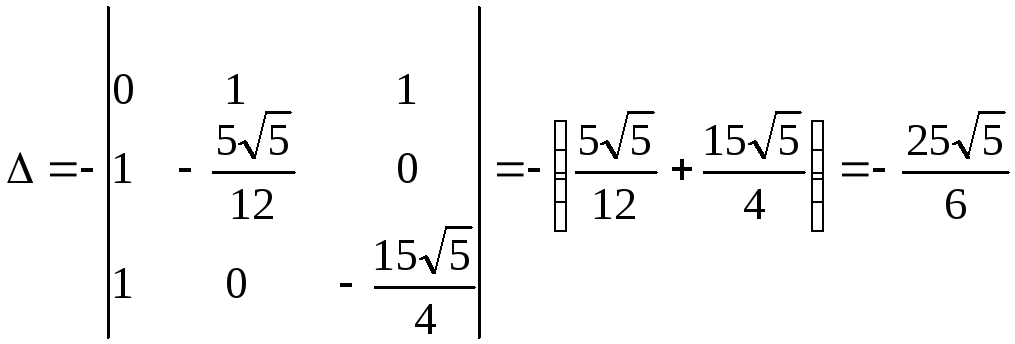 .
.
Так как дискриминант
функции Лагранжа в стационарной точке
![]() отрицателен, то в соответствии с
достаточным условием условного максимума
функция
отрицателен, то в соответствии с
достаточным условием условного максимума
функция
![]() имеет при
имеет при
![]() ,
,
![]() условный максимум. Значение целевой
функции в точке условного максимума
условный максимум. Значение целевой
функции в точке условного максимума
![]() .
.
Таким образом,
наибольшая суммарная прибыль
производственного объединения
![]() (млн.долл.) достигается при следующем
распределении денежных средств между
предприятиями:
(млн.долл.) достигается при следующем
распределении денежных средств между
предприятиями:
![]() млн.долл. и
млн.долл. и
![]() млн.долл.
млн.долл.
6. Оптимальное распределение капиталовложений. Метод динамического программирования
Задача 6. В
производственное объединение входят
при предприятия. Прирост продукции
каждого из них
![]() в зависимости от величины выделенных
предприятию капиталовложений
в зависимости от величины выделенных
предприятию капиталовложений
![]() указан в приведенной ниже таблице.
указан в приведенной ниже таблице.
|
|
|
||
|
предпр. 1 |
предпр. 2 |
предпр. 3 |
|
|
0 |
0 |
0 |
0 |
|
20 |
3 |
2 |
1 |
|
40 |
3 |
4 |
6 |
|
60 |
8 |
4 |
7 |
|
80 |
9 |
7 |
10 |
|
100 |
10 |
12 |
11 |
Требуется составить оптимальный план распределения капиталовложений между тремя предприятиями, обеспечивающий максимальное увеличение выпуска продукции всего производственного объединения.
Капиталовложения
![]() (в усл.ден.ед.) каждому предприятию могут
быть выделены только в размерах кратных
20 (усл.ден.ед.), и общий объем капиталовложений
составляет
(в усл.ден.ед.) каждому предприятию могут
быть выделены только в размерах кратных
20 (усл.ден.ед.), и общий объем капиталовложений
составляет
![]() (усл.ден.ед.).
(усл.ден.ед.).
Решить задачу о распределении денежных ресурсов методом динамического программирования
Решение.
Составим математическую модель данной задачи оптимального распределения ресурсов. Для этого сначала введем переменные:
![]() - количество
денежных средств, выделяемых
- количество
денежных средств, выделяемых
![]() -му
предприятию
-му
предприятию
![]() ;
;
![]() - соответствующий
прирост выпуска продукции
- соответствующий
прирост выпуска продукции
![]() -го
предприятия
-го
предприятия
![]() .
.
Затем запишем выражение целевой функции, имеющей смысл суммарного прироста выпуска продукции всего производственного объединения.
![]() (1)
(1)
Далее запишем ресурсное ограничение
![]()
![]() (2)
(2)
по смыслу задачи переменные должны быть неотрицательными:
![]() ,
,
![]() ,
,
![]() . (3)
. (3)
В результате получаем математическую формулировку задачи:
Найти такие значения
переменных
![]() ,
,
![]() ,
,
![]() ,
которые удовлетворяют ограничениям
(2), (3) и доставляют наибольшее значение
целевой функции (1).
,
которые удовлетворяют ограничениям
(2), (3) и доставляют наибольшее значение
целевой функции (1).
Решение поставленной задачи методом динамического программирования Беллмана содержит следующие основные этапы ([6]):
1) Вложение данной конкретной задачи в семейство подобных задач (инвариантное погружение задачи);
2) составление уравнения Беллмана, исходя из принципа оптимальности Беллмана;
3) Решение уравнения Беллмана4
4) Выделение решения исходной задачи из найденной функции Беллмана.
Перейдем к реализации указанных этапов.
1) Вместо одной
исходной задачи (1)-(3) с заданным значением
суммарного ресурса
![]() и числом предприятий
и числом предприятий
![]() рассмотрим семейство подобных задач с
изменяющимся значением суммарного
ресурса
рассмотрим семейство подобных задач с
изменяющимся значением суммарного
ресурса
![]()
![]() и изменяющимся числом предприятий
и изменяющимся числом предприятий
![]()
![]() :
:
![]() , (4)
, (4)
![]() , (5)
, (5)
![]()
![]() . (6)
. (6)
Введем функцию
2-х переменных
![]() - функцию Беллмана
- функцию Беллмана
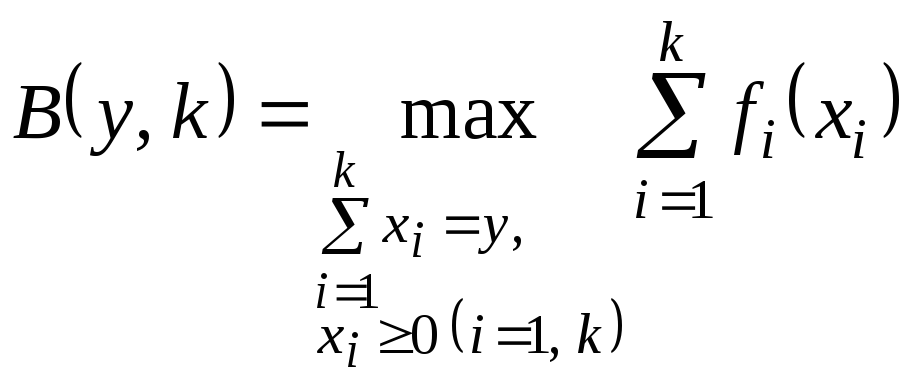 ,
,
которая имеет
смысл наибольшего суммарного прироста
продукции, достигаемого на
![]() предприятиях при использовании ресурса
в количестве
предприятиях при использовании ресурса
в количестве
![]() .
.
2) Принцип оптимальности многошагового процесса впервые был сформулирован Р. Беллманом и заключается в следующем: завершающая часть процесса должна быть оптимальной относительно текущего реализовавшегося состояния. Математическим выражением для данной задачи является уравнения Беллмана ([6]):
![]() ,
(8)
,
(8)
где
![]() ,
,
![]() .
.
3) Уравнение Беллмана имеет очевидное краевое условие
![]() (9)
(9)
Зная
![]() ,
из уравнения (8) последовательно находим:
,
из уравнения (8) последовательно находим:
![]() ,
,
где
![]() в силу краевого условия (9);
в силу краевого условия (9);
![]() .
.
При этом на каждом
шаге решается стандартная задача
нахождения функции одной переменной
![]() на отрезке
на отрезке
![]() .
.
Приведем табличную реализацию изложенного выше решения уравнения Беллмана.
4) Выделим решение
исходной задачи из найденной выше
функции Беллмана
![]() ,
организовав так называемую "попятную"
процедуру.
,
организовав так называемую "попятную"
процедуру.
Сначала найдем
оптимальное значение переменной
![]() .
Для этого в последнем соотношении для
.
Для этого в последнем соотношении для
![]() положим
положим
![]() :
:
![]() (10)
(10)
и найдем то значение
![]() на котором достигается максимум правой
части отношения (10). По таблице 2 определим
на котором достигается максимум правой
части отношения (10). По таблице 2 определим
![]() ,
и это наибольшее значение достигается
при
,
и это наибольшее значение достигается
при
![]() .
.
После выделения
![]() единиц ресурса третьему предприятию
на остальные два предприятия (второе и
первое) следует распределить оставшийся
ресурс
единиц ресурса третьему предприятию
на остальные два предприятия (второе и
первое) следует распределить оставшийся
ресурс
![]() .
.
Положим
![]() в предпоследнем соотношении для
в предпоследнем соотношении для
![]() :
:
![]() (11)
(11)
и найдем то значение
![]() ,
на котором достигается максимум в
правой части соотношения (11). По таблице
1 определяем
,
на котором достигается максимум в
правой части соотношения (11). По таблице
1 определяем
![]() ,
и это наибольшее значение достигается
при
,
и это наибольшее значение достигается
при
![]() .
.
Оптимальное
значение
![]() первой переменной найдем из условия
первой переменной найдем из условия
![]() ,
(12)
,
(12)
т.е.
![]() .
.
Таким образом, оптимальное решение исходной задачи о распределении ресурсов выражается равенствами
![]() ,
,
![]() ,
,
![]() (усл.ден.ед.)
(усл.ден.ед.)
7. Модель Леонтьева межотраслевого баланса
Задача 7. Некоторая
экономическая система задана матрицей
прямых затрат
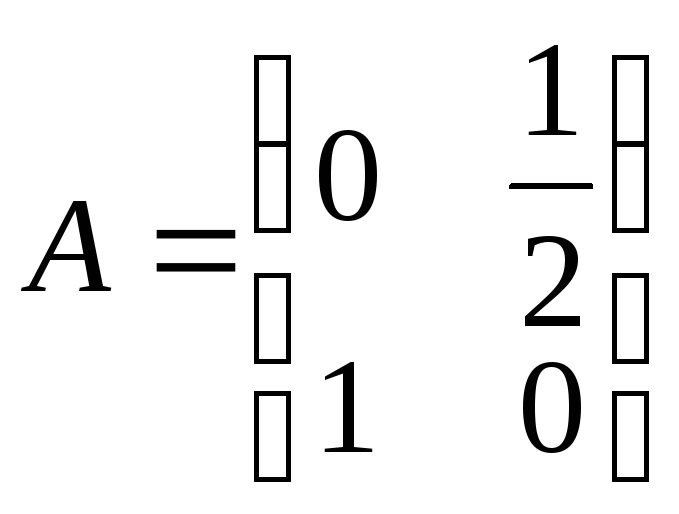 ,
вектором прямых потребностей в труде
,
вектором прямых потребностей в труде
![]() и вектором конечного потребления
и вектором конечного потребления
![]() .
.
Требуется:
1) Проверить
продуктивность модели Леонтьева
![]() ;
;
2) Вычислить косвенные потребности во всех продуктах, включая труд, для чистого выпуска единицы каждого продукта;
3) Найти нормализованный вектор равновесных цен и соответствующую ему ставку заработной платы;
4) Определить
суммарный выпуск каждой отрасли и
суммарную потребность в труде для
производства ассортиментного набора
продуктов
![]() .
.
Решение.
Развернутое изложение модели Леонтьева содержится в монографиях [2], [7]. Краткое описание этой модели приведено в методической разработке [8], терминологию и обозначения которую мы будем использовать в дальнейшем.
Матричная форма
записи модели Леонтьева (для рассматриваемого
в данной задаче случая двухотраслевой
экономики) имеет вид:
![]() ,
где
,
где
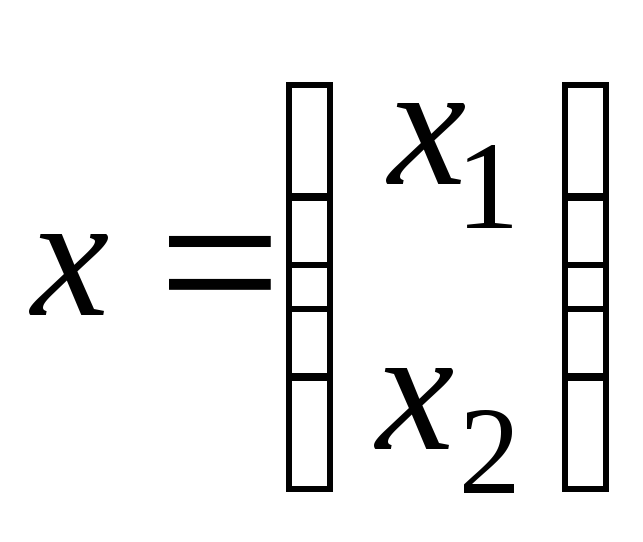 вектор (столбец) валового выпуска
продуктов,
вектор (столбец) валового выпуска
продуктов,
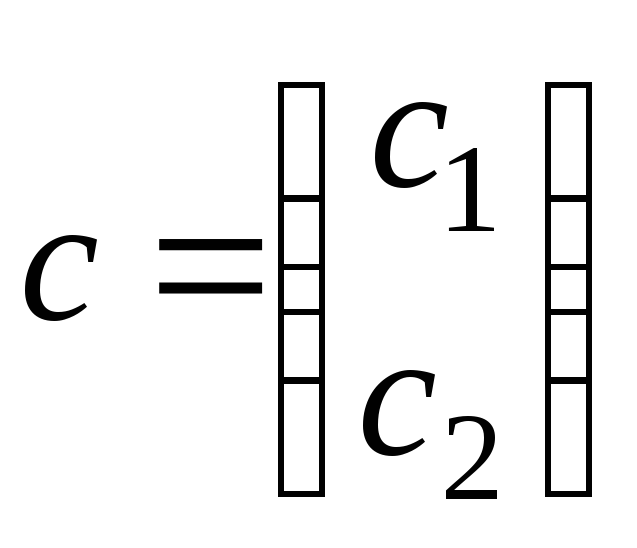 - заданный вектор (столбец) конечного
потребления продуктов,
- заданный вектор (столбец) конечного
потребления продуктов,
![]() - заданная матрица прямых затрат
продуктов.
- заданная матрица прямых затрат
продуктов.
1) Для проверки продуктивности модели Леонтьева применим следующий критерий продуктивности:
модель Леонтьева
продуктивна тогда и только тогда, когда
выполнено условие
![]() ;
где
;
где
![]() наибольшее положительное собственное
значение матрицы прямых затрат
наибольшее положительное собственное
значение матрицы прямых затрат
![]() .
.
Найдем собственные
значения матрицы
![]() ,
т.е. корни характеристического уравнения
,
т.е. корни характеристического уравнения
![]() :
:
 ,
,
![]() ,
,
![]() ,
,
![]() .
.
Таким образом
![]() ,
и условие
,
и условие
![]() выполнено, т.е. модель Леонтьева является
продуктивной.
выполнено, т.е. модель Леонтьева является
продуктивной.
2) Для нахождения
матрицы косвенных затрат продуктов
 применим формулу
применим формулу
![]() ,
где
,
где
![]() - так называемая матрица полных затрат
продуктов.
- так называемая матрица полных затрат
продуктов.
Последовательно находим:
 ;
;
 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
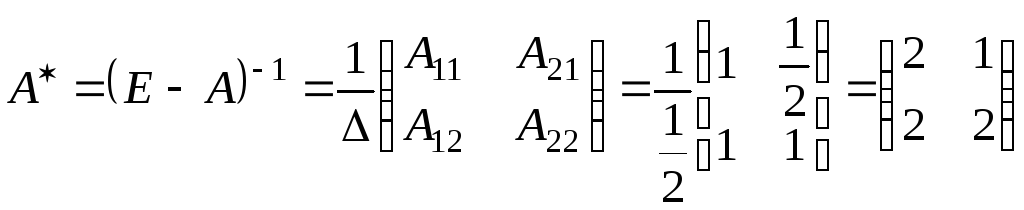 ;
;
 .
.
В результате получаем:
![]() (косвенные затраты
1-го продукта для чистого выпуска единицы
1-го конечного продукта);
(косвенные затраты
1-го продукта для чистого выпуска единицы
1-го конечного продукта);
![]() (косвенные затраты
1-го продукта для чистого выпуска единицы
2-го конечного продукта);
(косвенные затраты
1-го продукта для чистого выпуска единицы
2-го конечного продукта);
![]() (косвенные затраты
2-го продукта для чистого выпуска единицы
1-го конечного продукта);
(косвенные затраты
2-го продукта для чистого выпуска единицы
1-го конечного продукта);
![]() (косвенные затраты
2-го продукта для чистого выпуска единицы
2-го конечного продукта).
(косвенные затраты
2-го продукта для чистого выпуска единицы
2-го конечного продукта).
Далее найдем вектор
косвенных потребностей в труде
![]() для чистого выпуска единицы соответствующего
конечного продукта. Применим формулу
для чистого выпуска единицы соответствующего
конечного продукта. Применим формулу
![]() ,
где
,
где
![]() - вектор (строка) полных потребностей в
труде.
- вектор (строка) полных потребностей в
труде.
Последовательно находим:
![]() ,
,
![]() .
.
Следовательно,
![]() (косвенные затраты
труда для чистого выпуска единицы 1-го
конечного продукта);
(косвенные затраты
труда для чистого выпуска единицы 1-го
конечного продукта);
![]() (косвенные затраты
труда для чистого выпуска единицы 2-го
конечного продукта);
(косвенные затраты
труда для чистого выпуска единицы 2-го
конечного продукта);
3) Для нахождения
нормализованного вектора равновесных
цен на продукты
![]() и соответствующей ему ставки заработной
платы
и соответствующей ему ставки заработной
платы
![]() применим следующие формулы:
применим следующие формулы:
![]() ,
,
![]() ,
,
![]() ,
,
где
![]() ,
,
![]() координаты вектора полных потребностей
в труде.
координаты вектора полных потребностей
в труде.
Получаем:
![]() ;
;
![]() ,
,
![]() .
.
4) Вектор валового выпуска продуктов найдем по формуле
![]() :
:
![]() .
.
Таким образом,
![]() (количество
продукта, выпускаемое 1-ой отраслью);
(количество
продукта, выпускаемое 1-ой отраслью);
![]() (количество
продукта, выпускаемое 2-ой отраслью).
(количество
продукта, выпускаемое 2-ой отраслью).
Суммарная потребность
в труде для производства заданного
конечного продукта
![]() (трудоемкость производства) выражается
скалярной величиной
(трудоемкость производства) выражается
скалярной величиной
![]() .
.
Рекомендуемая литература
1. Малыхин В.И. Финансовая математика: Учеб. пособие для вузов. – 2-е изд., перераб и доп. – М.: ЮНИТИ – ДАНА, 2003. – 237 с.
2. Колемаев В.А. Математическая экономика: Учебник для вузов.– М.: ЮНИТИ, 1998. –240 с.
3. исследование операций в экономике: Учеб. пособие для вузов/ Под ред. проф. Н.Ш. Кремера.– М.: Банки и биржи, ЮНИТИ, 1999. – 407 с.
4. Исследование операций: основы теории и экономические приложения: Учеб. пособие.– Екатеринбург: Изд-во Урал.гос.проф.-пед.ун-та, 1996,–112 с.
5. Методические указания для выполнения контрольной работы по дисциплине "Математическое программирование" для студентов заочного обучения. – Екатеринбург, 2003.–27 с.
6. Габасов Р., Кириллова Ф.М. Методы оптимизации. -Мн.: Изд-во БГУ, 1975.– 280 с.
7.Ланкастер К. Математическая экономика.–М.: Сов. радио, 1972.
8. Методические указания для выполнения контрольной работы по дисциплине "Математическое моделирование экономических систем" для студентов заочного обучения.– Екатеринбург, 2003.–27 с.
