§ 6.1.5 Методы представления колебаний

Существуют различные методы описания гармонических колебаний. Приведём некоторые из них.

1. Аналитический метод

Задаётся уравнение колебаний гармонического осциллятора

х=Аsin(ωt+φ₀)

по которому и определяется смещение его от положения равновесия в любой момент времени.

2. Графический метод

Строятся график гармонического колебания (рис.6.4) х=Аsin(ωt+φ₀). По оси абсцисс (ОХ) откладывается время t или фаза колебаний ωt+φ₀, по оси ординат (ОУ) – смещение х от положения равновесия.

3. Метод векторной диаграммы

Этот метод состоит в следующем. Гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде А колебания, а направление образует с осью х угол, равный начальной фазе колебания (рис. 6.5). Если привести этот вектор во вращение с угловой скоростью ω₀, то проекция конца вектора на ось х будет перемещаться в пределах от +А до -А, а колеблющаяся величина будет изменяться со временем по закону

x = Asin(ω₀t+φ₀), совершая гармоническое колебание.

§ 6.1.6 Скорость и ускорение колеблющейся точки

Чтобы найти скорость материальной точки при гармоническом колебании, возьмем производную от смещения колеблющейся точки x = Asin(ω₀t+φ₀) по времени:

(6.18)

где υ_max = Аω₀ — максимальная скорость (амплитуда скорости).

На основании тригонометрических формул преобразуем (4.18):

(6.19)

Сравнивая выражения для смещения и скорости замечаем, что фаза скорости на больше фазы смещения, т.е. скорость опережает по фазе смещение на Продифференцировав (4.18), найдем ускорение:

(6.20)

где а_max = А ω₀² - максимальное ускорение (амплитуда ускорения).

Вместо (6.20) запишем

а = а_max соs [π + (ω₀t+φ₀)] (6.21)

Из сравнения (6.21) и (6.17) следует, что фазы ускорения и смещения различаются на π, т. е. эти величины изменяются в противофазе. Это значит, что при положительном максимальном смещении ускорение максимально, но отрицательно. На рисунке показаны графические зависимости смещения, скорости и ускорения от времени (рис.6.6, а) и их векторные диаграммы (рис.6.6, б) .

§ 6.1.7 Кинетическая и потенциальная энергии колебательного движения

Гармонический осциллятор обладает как кинетической, так и потенциальной энергией, которые последовательно переходят друг в друга при колебаниях осциллятора. Полная энергия осциллятора равна сумме кинетической и потенциальной энергии:

Е = Е_к+Е_п (6.22)

Кинетическая энергия осциллятора, колеблющегося по гармоническому закону, вычисляют по формуле:

(6.23)

с учётом mω² = k

Потенциальную энергию колебательного движения найдём, исходя из формулы для потенциальной энергии упругой деформации:

(6.24)

Складывая кинетическую и потенциальную энергию, получим полную механическую энергию материальной точки, колеблющейся по гармоническому закону:

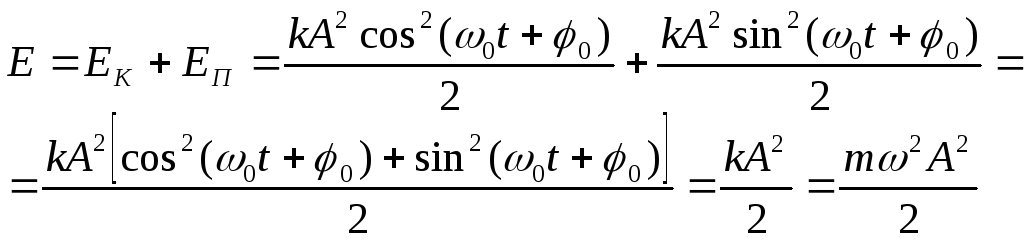(6.25)

Полученное выражение показывает, что энергия гармонического осциллятора от времени не зависит, т.е. с течением времени остаётся величиной постоянной, а зависит только от квадрата амплитуды и частоты.

При отсутствии сил трения полная механическая энергия системы не изменяется:

(6.26)

Графически зависимости кинетической, потенциальной и полной механической энергий колеблющейся системы от времени показаны на рис. 4.7, а.

Потенциальная яма (ограниченная область пространства, в которой потенциальная энергия меньше, чем в не её), соответствующая гармоническому колебанию, изображена на рис. 6.7, б. Она определяется зависимостью . Отложив на оси ординат полную механическую энергию Е, по графику определяют интервал координат (-А, +А), за пределы которого частица, обладающая такой энергией, выйти не может.