§ 9.3 Основное уравнение молекулярно-кинетической теории газов

Одним из первых и важных успехов молекулярно-кинетической теории было качественное и количественное объяснение явления давления газа на стенки сосуда.

Давление возникает в результате ударов молекул о стенки сосудов. Рассмотрим поведение одной произвольно выбранной молекулы иде­ального газа, находящейся в сосуде, имеющем форму куба (рис.9.11). Пустьυ_i — ее скорость, направленная перпендикулярно стенке сосуда, а m_i — масса. При упругом ударе молекула сообщает стенке импульс m_iυ_i после удара ее импульс станет равным - m_iυ_i. Следовательно, импульс молекулы изменится на m_iυ_i-(-m_iυ_i)= 2m_iυ_i. По второму закону Ньютона,

F_it_i =2 m_iυ_i. (9.17)

Если в кубе, длина ребра которого равна ℓ, находится n молекул, то вследствие беспорядочного движения молекул и равновероятности всех направлений можно считать, что 1/3N молекул движется вдоль оси X, 1/3N— вдоль оси Y, 1/3N молекул — вдоль оси Z. Чтобы найти среднюю силу давления газа, следует подсчитать сумму импульсов всех молекул, ударяющихся о стенку за определенное время. От удара до следующего удара о ту же грань молекула проходит путь, в среднем равный 2ℓ. Интервал времени между двумя этими ударами равен t_i = 2ℓ/υ_i. Определим теперь среднюю силу, с которой действует на одну из стенок сосуда одна молекула. В уравнение (9.17) подставим время t_i между двумя ударами:

(9.18)

откуда

или (9.19)

Молекулы газа движутся с различной скоростью (υ₁, ..., υ_i, ..., υ_n); следовательно, они сообщают стенке сосуда и раз­личные импульсы. Выберем какое-либо одно направление движения молекул (например, вдоль оси X). Между двумя противоположными гранями куба в этом направ­лении движется 1/3 всех молекул, и суммарная сила ударов об одну грань

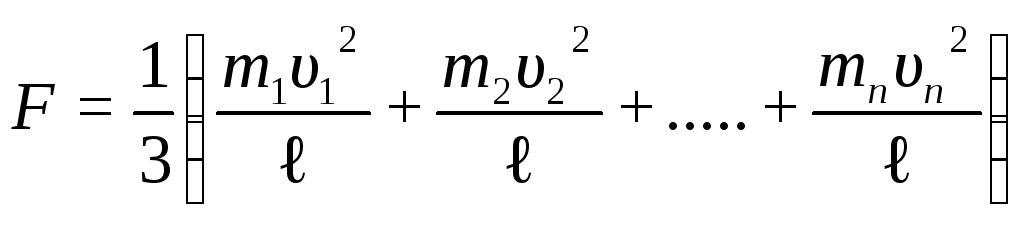(9.20)

В идеальном газе m₁ = m₂ = ... = m_n = m, поэтому

(9.21)

Умножив и разделив правую часть равенства на N, получим

(9.22)

Выражение, стоящее в скобках, есть квадрат средней квадратической скорости движения молекул . Таким образом,

(9.23)

Следовательно,

(9.24)

(9.25)

Тогда

(9.26)

Это основное уравнение молекулярно-кинетической теории

Оно определяет макроскопическую величину — давление газа через концентрацию n₀ молекул, массу m отдельных молекул и среднюю квадратическую скорость их движения.

Если через обозначить среднюю кинетическую энергию поступательного движения некой «средней» молекулы, то уравнение (9.26) можно записать в виде

(9.27)

Давление газа равно 2/3 от средней кинетической энергии поступа­тельного движения всех молекул, которые содержатся в единичном объ­еме газа.

Следствия, вытекающие из основного уравнения молекулярно-кинетической теории газов.

• Возьмем 1 моль газа, который занимает объем V. Плотность молекул газа 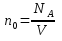и уравнение (9.27) можно записать в виде

(9.28)

Но для 1 моль справедливо уравнение состояния рV = RТ, откуда

Подставив это выражение для давления в уравнение (9.28) и решив его относительно Т или , получим чтотермодинамическая температура пропорциональна средней кинетической энергии хаотического движения молекул газа.

(9.29)

Из уравнения (9.29) следует, Чем быстрее движутся молекулы, тем выше температура. Из уравне­ния (9.29) находим

(9.30)

для любого газа, откуда следует что средняя кинетическая энергия молекул разных газов, находящихся при одинаковой температуре, равна между собой.

Из равенства средних кинетических энергий газовых молекул следует, что при перемешивании различных газов, имеющих одинаковые температуры, не происходит преимущественной передачи энергии от молекул одного газа молекулам другого.

Величина получила названиепостоянной Больцмана и представляет собой газовую постоянную, отнесенную к одной молекуле:

(9.31)

Следовательно, выражение (9.30) можно представить в виде

(9.32)

• Подставляя (9.32) в (9.27), находим выражение для давления газа:

Р = n₀kТ (9.33)

Давление газа пропорционально произведению числа молекул в единице объема на его термодинамическую температуру.

Анализ уравнения (9.32) показывает, что при Т=0К кинетическая энергия поступательного движения молекул Е=0, а следовательно, и = 0. Таким образом, при Т= 0 К отсутствует поступательное движение молекул.

Однако это не означает, что при Т=0К прекращается движение вообще. Сохраняются вращательное и колебательное движения атомов и молекул. По современным представлениям, при Т=0 К у атомов и еще более мелких частиц остается некоторая энергия, называемая нулевой.

Представим теперь формулу (9.32) в виде

(9.34)

откуда средняя квадратическая скорость

(9.35)

Отсюда следует: средняя квадратическая скорость молекул пропорциональна корню квадратному из термодинамической температуры.

На основании выражения (9.34) можно установить определение температуры: термодинамическая температура с точностью до постоянного множителя 3/2k равна средней кинетической энергии поступательного движения молекулы идеального газа.