§ 9.6 Барометрическая формула. Распределение Больцмана

При рассмотрении закона распределения Максвелла предполагалось, что молекулы равномерно распределяются по всему объему сосуда, что справедливо, если объем сосуда небольшой.

Для больших объемов равномерность распределения молекул по объему нарушается из-за действия силы тяжести, вследствие чего плот­ность, а следовательно, и число молекул в единице объема будут неодинаковым.

Рассмотрим молекулы газа, находящегося в поле тяготения Земли.

Выясним зависимость давления атмосферы от высоты над поверхно­стью Земли. Допустим, на поверхности Земли (h = 0) давление атмосфе­ры P₀. На высоте h оно равно P. При увеличении высоты на dh давление уменьшится на dP:

dP = - ρgdh (9.49)

[ρ — плотность воздуха на данной высоте, ρ = mn₀, где m — масса моле­кулы, n₀ — концентрация молекул].

Используя соотношение P = n₀kТ, получаем

тогда

(9.50)

Полагая, что на некоторой высоте h Т = соnst, g = соnst, разделяя пе­ременные, интегрируем выражение (9.50):

,

Получаем

(9.51) — барометрическая формула.

Барометрическая формула показывает зависимость давления газа от высоты над поверхностью Земли.

Если учесть, что концентрация молекул воздуха в атмосфере определяет дав­ление, то формулу (9.51) можно записать в виде

(9.52)

Из формулы (9.52) следует, что с понижением температуры число частиц на высоте, отличной от нуля, убывает и при Т = 0К обращается в нуль, т. е. при 0К все молекулы расположились бы на земной поверх­ности.

Так как потенциальная энергия молекул на различной высоте раз­лична и на высоте h определяется по формуле где Е_П = mgh, то [см.

(9.53)

— закон Больцмана, показывающий распределение участвующих в теп­ловом движении молекул в потенциальном поле сил, в частности в поле силы тяжести.

Методика решения задач

В задачах данного типа используют свойства распределения Максвелла и Больцмана.

Пример 3.3. Определите среднюю арифметическую скорость <υ˃ молекул идеального газа, плотность которого при давлении 35 кПа составляет 0,3 кг/м³.

Дано: Р=35кПа=35∙10³ Па; ρ=0,3 кг/м³.

Найти: <υ˃.

Решение: Согласно основному уравнению молекулярно-кинетической теории идеальных газов,

, (1)

где n – концентрация молекул; m₀- масса одной молекулы; <υ_кв˃.- средняя квадратичная скорость молекул.

Учитывая, что , а, получаем

Так как плотность газа

,

где m – масса газа; V - его объём; N - число молекул газа, уравнение (1) можно записать в виде

или . Подставляя это выражение в формулу (2), находим искомую среднюю арифметическую скорость:

Ответ: <υ˃=545 м/с.

Пример 3.5. Найти относительное число газа, скорость которого отличается не более чем на δη = 1% значения средней квадратичной скорости.

Дано: δη = 1%.

Найти:

Решение В распределении Максвелла

подставим значение

; δυ = υ_квδη.

Относительное число молекул будет

Ответ:

Пример 3.6. При какой температуре газа число молекул со скоростями в заданном интервале υ, υ + dυ будет максимальной? Масса каждой молекулы m.

Решение

Для нахождения искомой температуры необходимо исследовать функцию распределения Максвелла на экстремум .

.

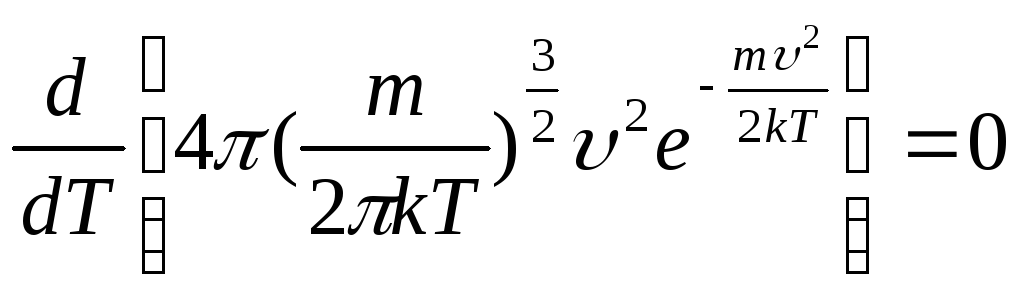
Пример 3.7. Вычислить наиболее вероятную, среднюю и среднюю квадратичную скорости молекул идеального газа, у которого при нормальном атмосферном давлении плотность ρ = 1кг/м³.

Решение

Умножив числитель и знаменатель в подкоренных выражениях (3.4) на число Авогадро N_а, получим следующие формулы для скоростей:

.

Запишем уравнение Менделеева-Клапейрона, введя в него плотность

ΡRT = MP

Определим отсюда величину и, подставив её в выражения, определяющие скорость молекул, получим:

Пример 3.4. Идеальный газ с молярной массой M находится в однородном поле тяжести, ускорение свободного падения в котором g. Найти давление газа как функцию высоты h, если при h = 0 давление Р = Р₀, а температура меняется с высотой как T = T₀(1 - α·h), где α – положительная постоянная.

Решение

При увеличении высоты на бесконечно малую величину давление получает приращение dP = - ρgdh, где ρ - плотность газа. Знак минус появился, так как с увеличением высоты давление уменьшилось.

Поскольку рассматривается идеальный газ, плотность ρ может быть найдена из уравнения Mенделеева-Клапейрона:

Подставим значение плотности ρ и температуры Т, получим разделяя переменные:

Интегрируя это выражение, находим зависимость давления газа от высоты h:

Так как при h = 0 Р = Р₀ получаем значение постоянной интегрирования С = Р₀. Окончательно функция Р( h ) имеет вид

Необходимо отметить, что, так как давление является величиной положительной, полученная формула справедлива для высот .

Пример. Французский физик Ж.Перрен, наблюдал под микроскопом изменение концентрации взвешенных в воде (ρ=1г/см³) шариков гуммигута (ρ ₁=1,25г/см³) с изменением высоты, экспериментально определил постоянную Авогадро. Определите это значение, если температура взвеси Т=298К, радиус шариков =0,21 мкм, а при расстоянии между двумя слоями Δh=30мкм число шариков гуммигута в одном слое в два раза больше, чем в другом.

Дано: ρ=1г/см³=1000кг/м³; ρ=1,25 г/см³=1250кг/м³; Т=280 К; r=0,21мкм=0,21∙10^-6 м; Δh=30мкм=3∙10^-5 м; .

Найти: N_A.

Решение. Барометрическую формулу

,

Используя уравнение состояния P=nkT, можно преобразовать для высот h₁ и h₂ к виду

и ,

где n₀, n₁ и n₂- соответственно концентрация молекул на высоте h₀, h₁ и h₂; М – молярная масса; g- ускорение свободного падения; R- молярная газовая постоянная.

Тогда

. (1)

Прологарифмировав выражение (1), получим

(2)

Масса частицы ; m=ρV=ρπr³. Подставив эти формулы в (2) и учитывая поправку на закон Архимеда, получим

Откуда искомое выражение для постоянной Авогадро

Ответ: N_A=6,02∙10²³моль^-1.

Пример. Какова температура Т азота, если средняя длина свободного пробега <ℓ˃ молекул азота при давлении Р=8кПа составляет 1мкм. Эффективный диаметр молекул азота d=0,38нм. .

Дано: <ℓ˃ =1мкм=1∙10^-6 м; Р=8кПа=8∙10³ Па; d=0,38нм=0,38∙10^-9м;

Найти: Т.

Решение. Согласно уравнению состояния идеального газа

P=nkT,

где n – концентрация молекул; k - постоянная Больцмана.

Средняя длина свободного пробега молекул газа

,

откуда . Подставив эту формулу в выражение (1), найдём искомую температуру азота

Ответ: Т=372 К.

Пример. При температуре Т=280 К и некотором давлении средняя длина <ℓ₁˃ свободного пробега молекул равна 0,1 мкм. Определите среднее число <z₂˃ столкновений молекул в 1с, если давление в сосуде уменьшить до 0,02 первоначального давления. Температуру считать постоянной, а эффективный диаметр молекулы кислорода принять равным 0,36нм .

Дано: Т=280 К; <ℓ₁˃ =0,1мкм=0,1∙10^-6 м; М=32∙10^-3 кг/моль; ; d=0,36нм=0,36∙10^-9м;

Найти: <z₂˃.

Решение. Среднее число <z₂˃ столкновений молекулы в 1с при конечном давлении определяется отношением средней скорости <υ˃. молекулы к средней длине её свободного пробега <ℓ₂˃. при том же давлении:

, (1)

где средняя скорость молекул определяется по формуле

(2)

где R – молярная газовая постоянная; М – молярная масса вещества.

Из формул иP=nkT следует, что средняя длина свободного пробега молекул обратно пропорциональна давлению:

,

откуда . Подставив это выражение в формулу (1) и учитывая (2), получаем искомое среднее число столкновений молекул в 1с:

Ответ: <z₂˃ = 8,61∙107с^-1.

Пример. Можно ли считать вакуум 100мкПа высоким, если он создан в колбе радиусом r=15 см, содержащей азот при 0ºС. Эффективный диаметр молекулы азота d=0,38нм. .

Дано: P=100мкПа=10^-4Па; r =15см=0,15 м; T=273 К; d=0,38нм=0,38∙10^-9м.

Найти:

Решение. Вакуум можно считать высоким, если средняя длина свободного пробега молекул газа гораздо больше линейных размеров сосуда, т.е. должно выполняться условие

˃˃2r

Средняя длина свободного пробега молекул газа

(учли P=nkT).

Вычисляя, получаем =58,8 м, т.е 58,8 м ˃˃0,3 м.

Ответ: да, вакуум высокий.