§21.6 Дифракция на пространственной решетке. Основы рентгеноструктурного анализа. Формула Вульфа–Брегга

Основная формула (21.5) дифракционной решетки может быть использована не только для определения длины волны, но и для решения задачи - нахождения постоянной дифракционной решетки по известной длине волны. Такая задача подводит к практически важному измерению параметров трехмерной кристаллической решетки посредством дифракции рентгеновских лучей, что является содержанием рентгеноструктурного анализа.

Если наложены друг на друга две дифракционные решетки с периодами с₁ т с₂, штрихи которых перпендикулярны, то для таких решеток условия главных максимумов имеют вид:

с₁ sinα₁ = ±k₁λ, с₂ sinα₁ = ±k₂λ. (21.21)

Углы α₁; α₂ отсчитываются во взаимно перпендикулярных направлениях. В этом

случае на экране появится система светлых пятен, каждому из которых соответствует пара значений k ₁ и k ₂ или α₁ и α₂. Таким образом, здесь можно найти с₁ и с₂„ по положению дифракционных пятен.

Если усложнить задачу, то по дифракционной картине можно измерить параметры и для трехмерной периодической структуры. Естественной объемной периодической структурой являются кристаллы, крупные молекулы и т. п.

Учитывая, что расстояние между рассеивающими центрами (атомами) в кристалле (10-¹⁰ м) приблизительно равно длине волны рентгеновского излучения, можно считать, что кристалл для этих лучей является трехмерной дифракционной решеткой.

На рисунке 21.9 штрихом показаны две соседние кристаллографические плоскости. Взаимодействие рентгеновских лучей с атомами и возникновение вторичных волн рассматривается как отражение от этих плоскостей. Пусть на кристалл под углом скольжения θ падают рентгеновские лучи 1 и 2; 1' и 2' - отраженные (вторичные) лучи. А₁В и А₁С - перпендикуляры к падающим и отраженным лучам соответственно. Разность хода отраженных (вторичных) лучей 1' и 2':

Δ = ВА₂ + А₂С = 2d sinθ,

где d - межплоскостное расстояние.

Максимумы интерференции при отражении возникнут в том случае, когда разность хода будет равна целому числу длин волн

2d sinθ = kλ (21.22)

где k = 1, 2, 3, ... . Это формула Вульфа - Брэгга.

П.Дебаем и П. Шеррером был предложен метод рентгеноструктурного анализа, основанный на дифракции монохроматических рентгеновских лучей на поликристаллических телах (обычно спрессованные порошки). В настоящее время широко применяют рентгеноструктурный анализ биологических (например белков) Этим методом Дж. Уотсон и Ф. Крик установили структуру ДНК, за что были удостоены Нобелевской премии.

Примеры решения задач.

Задача 1.На щель ширинойа= 0,05 мм падает нормально монохроматический свет (= 0,6 мкм). Определить угол отклонения лучей, соответствующих темной дифракционной полосе.

Решение.

Дано	Угол  отклонения лучей, соответствующий минимуму,
а = 510-5 м	определяется из условия
 = 610-7 м	, отсюда
k = 4
	При k = 4

, = 245

Задача 2.Чему равна постоянная дифракционной решетки, если для того, чтобы увидеть красную линию (= 0,7 мкм) в спектре третьего порядка, зрительную трубу пришлось установить под углом= 4836к оси? Какое число штрихов нанесено на 1 см длины этой решетки? Свет падает на решетку нормально.

Решение.

Дано	Условием получения дифракционного максимума является
 = 0,710-6 м	, отсюда
 = 4836	м = 2,8∙10-4 см
k = 3	Число штрихов на 1 см решетки
d, N

Задача 3.На дифракционную решетку в направлении нормали к ее поверхности падает монохроматический свет. Период решетки равен 2 мкм. Какого дифракционного порядка дифракционный максимум дает эта решетка в случае красного (= 0,7 мкм) света?

Решение.

Дано	Условием получения дифракционного максимума является
 = 0,710-6 м	, отсюда
d = 0,7∙10-7 м
k	Так как sin  ≤ 1, то

Если учесть, что порядок максимумов является целым числом, то для красного цвета k = 2.

Дано

k = 4

xk = 5∙10-2 м

 = 5∙10-7 м

d = 2∙10-5 м

L

Иначе, можно найти из АВС (рис.), в котором сторона АВ является частью экрана, расположенного на расстоянии от дифракционной решетки; в точке В наблюдает максимум нулевого порядка, в точке С – максимум четвертого порядка.

Таким образом , или

;

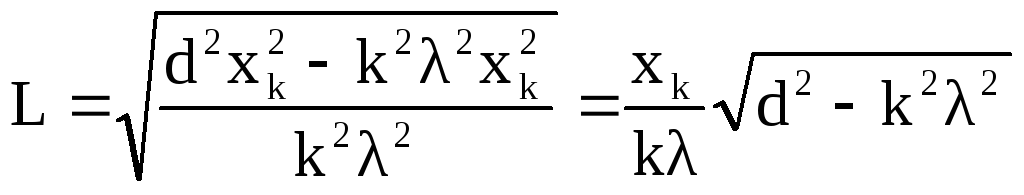м.