5. Дробно рациональные уравнения
.docxДробно рациональные уравнения. Решения
Уравнение
которые можно свести к дроби
f(x)/g(x)=0 называется дробно рациональным
уравнением.
Решение дробно
рациональных уравнений не слишком
сложная задача если Вы знаете методику,
а она достаточно проста.
Если
уравнение имеет несколько слагаемых
то переносим их по одну сторону знака
равенства и сводим к общему знаменателю.
В результате получим дробную функцию
f(x)/g(x), которая равна нулю
Следующим шагом находим корни числителя. Отвергаем среди них те, которые не принадлежат области допустимых значений (нули знаменателя) и записываем правильный ответ.
В теории все просто, однако на практике и у школьников и у студентов возникают проблемы при сведены к общему знаменателю, отыскании корней и т.д. Для ознакомления с решением рассмотрим несколько распространенных задач.
Примеры дробно рациональных уравнений
Пример
1.
Найти корни уравнения
Решение:
По методике переносим слагаемые и сводим
к общему знаменателю
Приравниваем
числитель и знаменатель к нулю и находим
корни. Первое уравнение можем решить
по теореме Виета
Второе
раскладываем на множители
Если от корней числителя отбросить нули знаменателя то получим только одно решение x=-7.
Внимание: Всегда проверяйте совпадают ли корни числителя и знаменателя. Если такие есть то не учитывайте их в ответе.
Ответ: х=-7.
------------------------------------
Пример
2. Решить уравнение
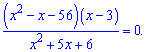
Решение:
Задано дробное рациональное уравнение.
Находим сначала корни числителя, для
этого решаем квадратное уравнение
Вычисляем
дискриминант
и
корни уравнения
Получили
три нуля числителя
.
Квадратное
уравнение в знаменателе проще и можем
решить по теореме Виета
Числитель
и знаменатель не имеют общих корней
поэтому все три найденные значения
будут
решениями.
------------------------------------
Пример
3. Найти корни уравнения
Решение:
Переносим слагаемое за знак равенства
и
сводим к общему знаменателю
Раскрываем в числителе скобки и сводим к квадратному уравнению
Полученное
дробно рациональное уравнение эквивалентно
системе двух уравнений
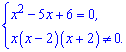
Корни
первого вычисляем через дискриминант
Нули
второго находим без проблем
Исключаем
из решений числителя значение
и
получим.
Ответ: х=3.
------------------------------------
Задачи на движение
Задача 4. Вертолет пролетел по ветру расстояние 120 км и обратно вернулся, потратив на весь путь 6 час. Найдите скорость ветра если скорость в штиль составляет 45 км/час.
Решение:
Обозначим скорость ветра через х
км/час. Тогда за ветром скорость вертолета
составит (45+х) км/час, и в обратном
направлении (45-х) км/час. По условию
задачи вертолет потратил 6 часов на
дорогу.
Разделив расстояние на
скорость и просуммировав получим время
Получили
дробно рациональное уравнение схема
решения которого неоднократно
повторялась
Решением второго уравнения будут значения x=-45; x=45.
Корни
числителя найдем после упрощений
С физических соображений первое решение отвергаем.
Ответ: скорость ветра 15 км/час.
------------------------------------
Задачи о совместной работе
Задача 2. Два лесорубы работая вместе выполнили норму вырубки за 4 дня. Сколько дней нужно на выполнение этой работы каждому лесорубу отдельно если первому для вырубки нормы нужно на 6 дней меньше чем другому?
Решение:
Пусть первый лесоруб выполняет норму
по х дней. Тогда второму необходимо
(х+6) дней.
Это означает что за один
день первый выполнит
,
а второй - 
часть всей нормы. По условию выполняют
норму за 4 дня, то есть оба в день могут
выполнить
нормы.
Составляем
и решаем уравнение
Данное
дробно рациональное уравнение эквивалентно
системе двух уравнений
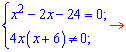
Одно
решение
не
соответствует физической сути задачи.
Время второго лесоруба
х+6=6+6=12 (дней)
Ответ: Работу первый лесоруб выполнит за 6 дней, а второй за 12.
------------------------------------
Подобных дробно рациональных уравнений можно рассмотреть множество, схема их решения неизменна. В теоретических задачах правильно составляйте уравнение и не заблуждайтесь при сведении к общему знаменателю. Все остальное сводится к решению преимущественно линейных или квадратных уравнений.
Следует приобрести навык в решении дробно-рациональных уравнений путём выполнения ряда тренировочных упражнений. Тренировочные упражнения предлагаются трёх уровней сложности: А – обязательный минимум знаний по этой теме, В – упражнения среднего уровня сложности, С – упражнения повышенной степени сложности.
|
№ |
Уравнения |
Ответы |
|
Уровень А |
||
|
1 |
|
5 |
|
2 |
|
-2; 50 |
|
3 |
|
-9; 1 |
|
4 |
|
-0,5; 1 |
|
5 |
|
0,5 |
|
6 |
|
-1 |
|
7 |
|
-4,7; -1 |
|
8 |
|
-4; 7 |
|
9 |
|
- |
|
10 |
|
2 |
;
6
|
№ |
Уравнения |
Ответы |
|
Уровень В |
||
|
1 |
|
7 |
|
2 |
|
-0,25 |
|
3 |
|
Нет корней |
|
4 |
|
0; 1 |
|
5 |
|
-1; 5 |
|
6 |
|
-1 |
|
7 |
(x+4)(x2-1)
=4x2
+ 24x
-
|
5 |
|
8 |
|
- |
|
9 |
|
4 |
|
10 |
|
1 |
|
№ |
Уравнения |
Ответы |
|
Уровень С |
||
|
1 |
|
-2 |
|
2 |
|
1; 4;
|
|
3 |
x2+x+1= |
-2; 1 |
|
4 |
|
1; 8 |
|
5 |
x2-5x+ |
1; 2; 3; 4 |
|
6 |
|
2 |
|
7 |
|
|
|
8 |
|
-3; 1 |
|
9 |
|
0,2; 1 |
|
10 |
|
Нет корней
|
