16. Геометрическая оптика как предельный случай волновой оптики.

Уравнения Эйкона.

Эйкология (от греч.Эйкон-изображено)

Волновое у-е для световой волны в среде с показателем преломления n=c\v. ²Ф - =0

Для монохроматической волны Ф(r,t)=(r)exp{-it}; ²+n²=0, где к₀=\с- волновое число в вакууме.

Волновое число в среде к= nк₀

₌(ln)+(ln)² ²(ln)+[(ln)]²+=0

Решение ищем: ()=A()exp{is()}

Вещественная скалярная ф-ия S() называется эйконалом (от греч. Eikon-изображения)

²(lnA)+[(lnA)]²-[S]²+n²+i{²S+2(lnA)S}=0

Приравниваем вещественную и мнимую часть получим два у-я для оредел. A() и S():

{

Для оптического диапазона длина волны много меньше расстояния L, на которых амплитуда волны существенно меняется (порядка размера оптических элементов). Поэтому первыми двумя слагаемыми в первом уравнении () можно пренебречь (их сумма имеет порядок 1/L²). Тогда это уравнение в оптическом диапазоне принимает вид: [S]²=n²

Это уравнение называется уравнением эйконала.

Градиент от функции S(r) направлен по нормали к поверхности S=const. Поэтому эйконал S описывает поверхности постоянной фазы волны, а ÑS приводит к понятию луча, т.е. к представлению о движении световой энергии в данной точке в определенном направлении. Лучом называется линия, касательная к которой совпадает в каждой точке с вектором ÑS. Распространение света рассматривается как движение световой энергии по лучам. Плоскость, перпендикулярная лучам света (где S = const), называется волновым фронтом.

Анализ распространения света в лучевом приближении составляет предмет геометрической оптики. Этот подход оправдан всегда, когда.

Физически этот член описывает искривление материальными объектами световых лучей, т.е. дифракцию света. Исходя из этого, можно сказать, что в геометрической оптике не учитываются дифракционные эффекты.

Принцип Ферма. В однородной среде S=k×r (k=const) и лучи являются прямыми параллельными линиями, а фронт волны – плоскостью, перпендикулярной лучам.

Для неоднородной среды лучи имеют более сложную конфигурацию. Пусть точки P₁ и P₂ соединяются лучом L (рис.5.1). Вычислим изменение фазы вдоль луча. Для каждой его точки имеем:

где dr направлен по лучу и совпадает с ÑS, dl – элемент длины пути. Для изменения фазы находим:

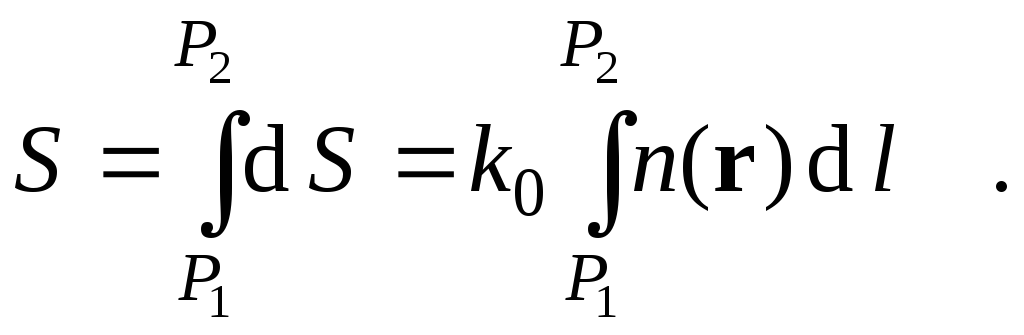
Интегрирование идет вдоль луча. Интеграл в (5.12) называется оптической длиной пути. Из (5.12) следует, что оптические длины путей вдоль различных лучей между точками волнового фронта в два момента времени одинаковы. Для любой другой кривой, соединяющей точки P₁ и P₂ , оптическая длина пути оказывается больше, чем для реального луча.

Принцип Ферма утверждает, что интеграл в (5.12) вдоль луча имеет стационарное значение, т.е. первая вариация dS относительно соседних путей интегрирования равна нулю. Или то же самое в другой формулировке: реальный луч отличается от остальных кривых, соединяющих две заданные точки, тем, что соответствующая ему оптическая длина имеет стационарное значение, т.е. малое изменение траектории не приводит к изменению оптической длины.

К принципу Ферма можно подойти и с другой стороны. Учтем что dt=dl / v – время прохождения пути dl со скоростью v, а n(r) = c / v(r). Тогда 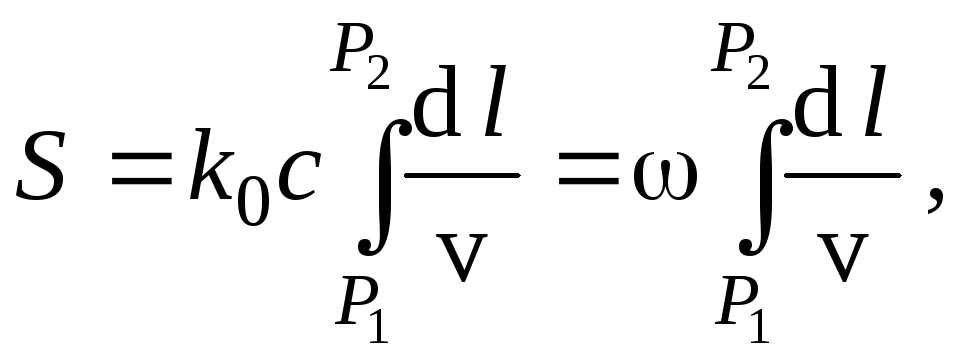(5.13)

где интеграл здесь дает время, затрачиваемое на прохождение пути от P₁ и P₂. С этой точки зрения принцип Ферма звучит так: лучом, соединяющим две точки, является тот путь, который делает стационарным время, затрачиваемое светом на его прохождение. Формулировка о стационарности времени прохождения пути между двумя точками, с одной стороны, утверждает экстремальный характер этого времени, а с другой стороны, не исключает наличия нескольких путей с одинаковым временем прохождения.

Например, в геометрической оптике все лучи от точки предмета идут по различным путям и встречаются в точке изображения. Но все они затрачивают одно и то же время на прохождение своего пути. Другими словами, оптические длины всех путей, соединяющих точку предмета с точкой изображения, одинаковы (принцип таутохронизма).