
- •1. Характеристика оптического диапазона электромагнитных волн. Особенности видимого диапазона
- •3. Т.К. K, w, m0, e0 – вещественные величины, то это значит, что e и b в плоской эмв колеблются в одинаковой фазе.
- •Складывая почленно (2.55) и (2.56) и обозначив
- •7. Волна с круговой или эллиптической поляризацией как суперпозиция волн с линейными поляризациями и линейно поляризованная волна как суперпозиция волн с круговой поляризацией.
- •8. Понятие дисперсии света. Классическая электронная дисперсия.
- •9 Нормальная и аномальная дисперсия.
- •10. Модулированные волны и волновые пакеты. Распространение волновых пакетов в диспергирующей среде. Групповая и фазовая скорость. Формула Рэлея.
- •11 Отражение и преломление света на границе двух диэлектриков.
- •13.Энергетические и фазовые соотношения при преломлении света на границе раздела двух сред. Явление Брюстера.
- •14.Полное внутреннее отражения. Примеры его проявления и использования.
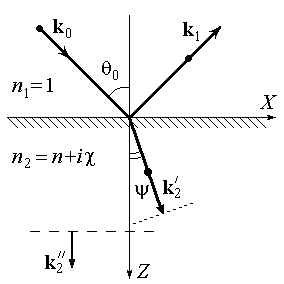
- •15. Распространение света в проводящих средах. Комплексный показатель преломления. Отражение света от поверхности проводника. Глубина проникновения. Закон Бугера.
- •16. Геометрическая оптика как предельный случай волновой оптики.
- •17.Центрированные оптические системы. Параксиальное приближение. Кардинальные элементы оптической системы.
- •18. Линза, её основные элементы. Тонкие и толстые линзы. Фокусное расстояние линзы. Построение изображения в оптических системах.
- •19. Оптические приборы.
- •24 Многолучевая интерференция.
- •28 Дифракционная решетка.
- •29. Критерий рэлея. Дисперсионная область и разрешающая спрособность дифракционной решётки.
- •30. Принципы голографической записи изображений. Схемы записи и воспроизведения голограмм.
- •31. Анизотропные среды. Тензор диэлектрической проницаемости. Распространение плоской электромагнитной волны в анизотропной среде. Эллипсоид лучевых скоростей.
- •32. Оптическая ось. Двуосные и одноосные кристаллы. Двойное лучепреломление. Обыкновенный и необыкновенный лучи. Поляризация при двойном лучепреломлении.
- •33. Поляроиды. Поляризационные и двоякопреломляющие призмы.
13.Энергетические и фазовые соотношения при преломлении света на границе раздела двух сред. Явление Брюстера.
Энергет.коэф.
отражения называется абсолютное значение
отношения нормальных компонент
векторов.Пластина в отраж.и падающ.волнах:
R=![]() =
=![]() Энергет.коэф. пропускания вводится
аналогичным образом для преломленной
волны: τ=
Энергет.коэф. пропускания вводится
аналогичным образом для преломленной
волны: τ=![]() =
=![]() ,
, ![]() cosϴ0
cosϴ0
H0n=H1 cosϴ0
H2n=H2 cosϴ2
R=![]() 2
τ=
2
τ=![]() =
=![]() 2
2
Энергетическое соотношение при преломлении и отражении
R5=![]() 2
R6=
2
R6=![]() 2
2
ᴊ9=![]() ᴊP=
ᴊP=![]()
При ϴ0=0 для μ1= μ2

R*ᴊ=1
R=![]() 2
ᴊ=
2
ᴊ=![]()
Энергетические
соотношения при преломлении и отражении.
Энергетическим
коэффициентом отражения
![]() называется абсолютное значение отношения
нормальных компонент векторов Пойнтинга
в отраженной и падающих волнах:
называется абсолютное значение отношения
нормальных компонент векторов Пойнтинга
в отраженной и падающих волнах:
![]()
Энергетический
коэффициент пропускания
![]() вводится аналогичным образом для
преломленной волны:
вводится аналогичным образом для
преломленной волны:
![]() (4.73)
(4.73)
Т.к.![]() ,(4.74)
,(4.74)![]() ,то
дляÂ
имеем:
,то
дляÂ
имеем:![]() ,
,![]()
Получим: ;
; ;
;![]()
![]()
При q0 = 0 для m1 = m2
 ;(4.82)
;(4.82)![]() .(4.83)
.(4.83)
Прямой проверкой
можно показать, что
![]() .
.
Это выражает закон
сохранения энергии при отражении и
преломлении света на границе раздела
двух сред. Графики для
![]() изображены на рис.4.11.
изображены на рис.4.11.
Явление Брюстера.
Для p–поляризованной
волны при некотором угле падения 0=б
назыв.углом Брюстера, отраженная волна
отсутствует, т.е.
![]() .
Это явление называетсяявлением
Брюстера.
.
Это явление называетсяявлением
Брюстера.
При переходе через
угол Брюстера фаза колебаний отраженной
волны скачком меняется на ![]() .Заметим,
что явлении Брюстера наблюдается тогда,
когда
направления преломленной и отраженной
волны ортогональны: Если
связывать наличие отраженной волны с
вынужденными колебаниями электронов
во второй среде, то в направлении,
перпендикулярном преломленной волне,
не должна распространяться энергия,
т.к. образующийся при этом диполь не
излучает в направлении собственных
колебаний.
.Заметим,
что явлении Брюстера наблюдается тогда,
когда
направления преломленной и отраженной
волны ортогональны: Если
связывать наличие отраженной волны с
вынужденными колебаниями электронов
во второй среде, то в направлении,
перпендикулярном преломленной волне,
не должна распространяться энергия,
т.к. образующийся при этом диполь не
излучает в направлении собственных
колебаний.
При
![]() при падающей волне с произвольным
азимутом отражается лишьs
– поляризованная компонента. Это
является одним из способов получения
линейно-поляризованного света.
при падающей волне с произвольным
азимутом отражается лишьs
– поляризованная компонента. Это
является одним из способов получения
линейно-поляризованного света.
Пример.
Стопа Столетова. При нормальном падении
света (![]() )
понятияs– и
p–
поляризаций теряют смысл и дают один и
тот же результат (для диэлектрика
)
понятияs– и
p–
поляризаций теряют смысл и дают один и
тот же результат (для диэлектрика
![]() ):
): (4.70)
– (4.71)
(4.70)
– (4.71)
14.Полное внутреннее отражения. Примеры его проявления и использования.


При падении света
на границу двух диэлектриков, для которых
![]() ,
из з. Снеллиуса
следует,что существует предельный (или
угол ϴn
падения, при котором угол преломлений:
ϴ2=
,
из з. Снеллиуса
следует,что существует предельный (или
угол ϴn
падения, при котором угол преломлений:
ϴ2=![]() ),
тогда sinϴn=
),
тогда sinϴn=![]() .
.
ϴ0≤ ϴn- угол преломления ϴ2 имеет обычную геометрическую интерпретацию, и коэффициенты R и T являются вещественными.
Когда угол падения
![]() ,
не существует вещественного угла
преломленияq2
, т.к. закон Снеллиуса дает для
,
не существует вещественного угла
преломленияq2
, т.к. закон Снеллиуса дает для
sin ϴ2
значение
больше единицы, а для cosq2
– чисто мнимое значение:
(таким образом, формулы Френеля обеспечивают выполнение граничных условий и в этом случае).
Рассмотрим сначала световую волну во второй среде (преломленную) в общем случае:

В такой записи
сомножитель I означает комплексную
амплитуду волны II, распространяющейся
вдоль оси X
со скоростью
![]() .
.


Знак (+) в первой экспоненте соответствует безграничному возрастанию поля в среде, что лишено физического смысла. Поэтому остается (–), что соответствует быстро убывающей с ростом z амплитуде волны, распространяющейся во второй среде вдоль X. Практически эта неоднородная волна существует лишь в поверхностном слое второй среды толщиной порядка длины волны. Причем фазовая скорость этой неоднородной (и соответственно не плоской) зависит как от свойств среды, так и от угла падения.
Формулы Френеля для отраженной волны имеют вид:
 ;
;
 .
.
 Видно,
что энергетические коэффициенты
Видно,
что энергетические коэффициенты![]() при углах падения больше критического.
Поэтому это явление называетсяполным
внутренним отражением
(ПВО). При
этом волна и соответствующая доля
энергии проникают через границу раздела
во вторую среду на некоторую глубину d
(глубину
проникновения)
(амплитуда поля на глубине d
падает в е раз):
при углах падения больше критического.
Поэтому это явление называетсяполным
внутренним отражением
(ПВО). При
этом волна и соответствующая доля
энергии проникают через границу раздела
во вторую среду на некоторую глубину d
(глубину
проникновения)
(амплитуда поля на глубине d
падает в е раз):
движутся вдоль поверхности раздела и затем возвращаются в первую среду. Места входа энергии во вторую среду и ее возвращения в первую смещены друг относительно друга. Амплитуды p– и s–компонент отраженной волны не изменяются по абсолютному значению, но испытывают различные фазовые сдвиги. Если представить, что
![]()
то

![]() .
.
Обозначим
![]()
Тогда .
.
Примеры:1. Призма–крыша. 2.Световоды. 3.Миражи.
4.Ромб (параллелепипед)
Френеля (![]() ).
).
![]()
![]()
