7. Волна с круговой или эллиптической поляризацией как суперпозиция волн с линейными поляризациями и линейно поляризованная волна как суперпозиция волн с круговой поляризацией.

Основные случаи поляризации:

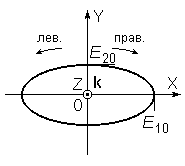
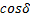1. =0

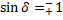
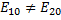
– эллиптическая поляризация

Если при наблюдении навстречу волне вращения вектора в фиксированной плоскости (перпендикулярна волновому вектору) происходит по часовой стрелке, то такая волна называется правой эллиптически поляризованной волной, если против часовой левой.

=0

эллипс вырождается в окружность. Такая поляризация называется круговой или циркулярной. Понятия правой и левой круговой поляризации применимы здесь аналогично определенным выше для эллиптической поляризации.

3. 0 (общий случай)

Главные оси эллипса не совпадают с осями координат. Ориентация зависит от сдвига фаз . Эллиптичность поляризаций

4. Линейная поляризация =0

Конец суммарного вектора электрического поля движется вдоль соответствующего отрезка прямой. Получаемая линейно поляризованная волна является предельным случаем эллиптически поляризованной волны. Видно, что световая волна с любой поляризацией может быть представлена в виде суперпозиции двух линейно поляризованных во взаимно-перпендикулярных плоскостях волн. Поэтому можно сказать, что электромагнитные волны обладают двумя независимыми состояниями поляризации.

Рассмотрим противоположный случай – суперпозицию волн с левой и правой круговыми поляризациями. Пусть при некоторой фиксированной координате z заданы компоненты их полей E₁ (левая) и E₂ (правая):

; ; ;

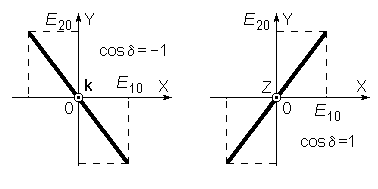
В результате их суперпозиции получается линейно поляризованная волна с E_x=E_1x+E_2x=2E_ocos wt E_y=E_1y+E_2y=0 Если между двумя круговыми волнами есть сдвиг фаз, то результирующий вектор линейно поляризованной волны будет колебаться в плоскости, расположенной под некоторым углом к оси X.

8. Понятие дисперсии света. Классическая электронная дисперсия.

Дисперсия света – зависимость скорости распространения световых волн и их частот.

Дисперсия появляется лишь в распространение немонохроматических волн, так ее монохроматические составляющие с различными частотами распространяются с различными скоростями. Дисперсия является следствием зависимости поляризованности атомов от частоты. Для нахождения явного вида входящей в математическое уравнение воспользуемся микроскопически классической теорией взаимодействия эл. Маг. Поля волны с веществом. Микроскопическая теория исходит из идеализации модели строения вещества. Наибольшей простотой отличается модель газообразной среды, т.к. для нее в первом приближение можно не учитывать взаимодействие атомов или молекул и считать, что действительно на отдельный атом поля совпадает со средним полем ЭВМ. В таких условиях для получения макроскопического матер. уравнения достаточно рассмотреть действие поля ЭВМ на изолированный атом.

Классическая электронная дисперсия

(1) уравнение вынужденных колебаний

В классической электронной дисперсии электрон, с которым взаимодействует электромагнитное поле (внешний или оптический электрон), в атоме рассматривается как затухающий дипольный асциллятор, характерный определенной собственной частотой w_o и постоянной затухающий

Уравнение движения в поле E(t)=E_o*e^-jwt свет волна имеет вид (1)

где r – смещение электрона из положения равновесия, e и m – заряд и масса электрона

Решение:

Дипольный момент атома p(t) индуцированный полем E(t) Если N – концентрация электронов в собственной частотой колебаний w_o, то поляризованность ( поляризация) Р среды определяется как С другой стороны

где - линейная диэлектрическая восприимчивость среды, которая в общем случае зависит от частоты w. Векторы связаны соотношением

отношение диэлектрической проницаемости

показатель преломления, а следовательно и скорость ЭВМ зависят от частоты, n – комплексная величина

; ;

Для прозрачных или частично прозрачных в оптическом диапазоне диэлектриков ;

Для различных ансамблей электронов с собственными частотами w₀ и концентрацией N_i