
- •1. Характеристика оптического диапазона электромагнитных волн. Особенности видимого диапазона
- •3. Т.К. K, w, m0, e0 – вещественные величины, то это значит, что e и b в плоской эмв колеблются в одинаковой фазе.
- •Складывая почленно (2.55) и (2.56) и обозначив
- •7. Волна с круговой или эллиптической поляризацией как суперпозиция волн с линейными поляризациями и линейно поляризованная волна как суперпозиция волн с круговой поляризацией.
- •8. Понятие дисперсии света. Классическая электронная дисперсия.
- •9 Нормальная и аномальная дисперсия.
- •10. Модулированные волны и волновые пакеты. Распространение волновых пакетов в диспергирующей среде. Групповая и фазовая скорость. Формула Рэлея.
- •11 Отражение и преломление света на границе двух диэлектриков.
- •13.Энергетические и фазовые соотношения при преломлении света на границе раздела двух сред. Явление Брюстера.
- •14.Полное внутреннее отражения. Примеры его проявления и использования.
- •15. Распространение света в проводящих средах. Комплексный показатель преломления. Отражение света от поверхности проводника. Глубина проникновения. Закон Бугера.
- •16. Геометрическая оптика как предельный случай волновой оптики.
- •17.Центрированные оптические системы. Параксиальное приближение. Кардинальные элементы оптической системы.
- •18. Линза, её основные элементы. Тонкие и толстые линзы. Фокусное расстояние линзы. Построение изображения в оптических системах.
- •19. Оптические приборы.
- •24 Многолучевая интерференция.
- •28 Дифракционная решетка.
- •29. Критерий рэлея. Дисперсионная область и разрешающая спрособность дифракционной решётки.
- •30. Принципы голографической записи изображений. Схемы записи и воспроизведения голограмм.
- •31. Анизотропные среды. Тензор диэлектрической проницаемости. Распространение плоской электромагнитной волны в анизотропной среде. Эллипсоид лучевых скоростей.
- •32. Оптическая ось. Двуосные и одноосные кристаллы. Двойное лучепреломление. Обыкновенный и необыкновенный лучи. Поляризация при двойном лучепреломлении.
- •33. Поляроиды. Поляризационные и двоякопреломляющие призмы.
Складывая почленно (2.55) и (2.56) и обозначив
![]() (2.57)
получаем:
(2.57)
получаем:
 (2.58)
(2.58)
Две плоские монохром. бегущие ЭМВ с одинаковой частотой, распростр. в одном и том же напр., в результате сложения дают плоскую монохроматическую ЭМВ той же частоты, распр. в том же направлении.
Биения. Рассмотрим случай, когда w1 ¹ w2 , E1 || E2 :
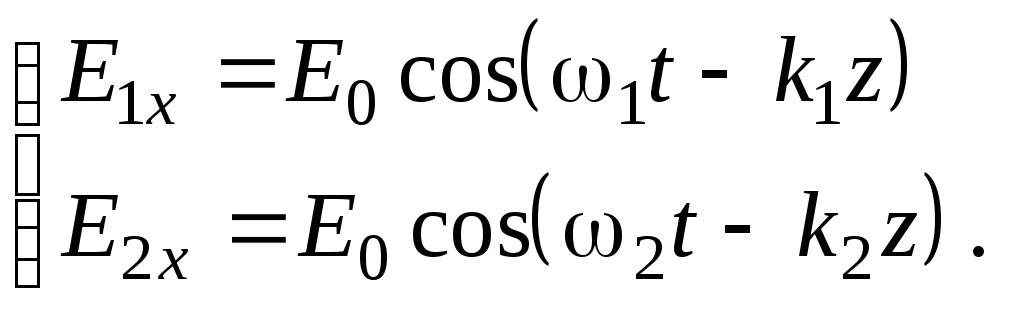 (2.59)
(2.59)
В соответствии с
принципом суперпозиции имеем: (2.60)
(2.60)
Мы получили
незатухающую бегущую в сторону +Z
немонохроматическую
волну. Т.к.
в оптическом диапазоне обычно | w1
– w2
| <<
w1
+ w2
, то сомножитель
![]() в (2.60) является медленно меняющейся
амплитудой ЭМВ с частотой (w1
+ w2)
/ 2 (см. рис.2.3). Гармонические колебания
с медленно изменяющейся амплитудой
называются биениями.
Понятие «медленно изменяющаяся амплитуда»
определяется относительно основного
гармонического колебания: амплитуда
мало меняется в течение многих периодов
основного гармонического колебания.
Частота W
= |w1
– w2|
называется частотой
биений.
Стоячие
волны.
Рассм.
суперпозицию двух монохроматических
волн с w1
= w2
= w
, E10
= E20
= E0
,
E1
||
E2
и распространяющихся навстречу друг
другу:
в (2.60) является медленно меняющейся
амплитудой ЭМВ с частотой (w1
+ w2)
/ 2 (см. рис.2.3). Гармонические колебания
с медленно изменяющейся амплитудой
называются биениями.
Понятие «медленно изменяющаяся амплитуда»
определяется относительно основного
гармонического колебания: амплитуда
мало меняется в течение многих периодов
основного гармонического колебания.
Частота W
= |w1
– w2|
называется частотой
биений.
Стоячие
волны.
Рассм.
суперпозицию двух монохроматических
волн с w1
= w2
= w
, E10
= E20
= E0
,
E1
||
E2
и распространяющихся навстречу друг
другу:
 (2.61)
(2.61)
где d – разность фаз. Тогда
![]() (2.62)
(2.62)
Сомножитель
![]() с точностью до знака можно рассматривать
как амплитуду колебаний напряженности
поля в заданной точкеz
. Она изменяется от точки к точке по
гармоническому закону. Напряженность
во всех точках
изменяется
с одинаковой частотой в одной фазе.
Такая волна называется стоячей.
В точках оси Z,
где
с точностью до знака можно рассматривать
как амплитуду колебаний напряженности
поля в заданной точкеz
. Она изменяется от точки к точке по
гармоническому закону. Напряженность
во всех точках
изменяется
с одинаковой частотой в одной фазе.
Такая волна называется стоячей.
В точках оси Z,
где
![]() полеE =
0 (такие точки называются узлами).
В точках оси Z,
где
полеE =
0 (такие точки называются узлами).
В точках оси Z,
где
![]() полеE
– максимально (такие точки называются
пучностями).
Расстояние между узлами (или пучностями)
равняется половине
длины бегущей волны
– l/2.
Кроме того, колебания напряженности во
всех точках стоячей волны в некоторый
момент времени находятся в одной и той
же фазе (например, E
= 0 во всех z
при
полеE
– максимально (такие точки называются
пучностями).
Расстояние между узлами (или пучностями)
равняется половине
длины бегущей волны
– l/2.
Кроме того, колебания напряженности во
всех точках стоячей волны в некоторый
момент времени находятся в одной и той
же фазе (например, E
= 0 во всех z
при
![]() ),
тогда как колебания напряженности
электрического поля в различных точках
бегущей волны не совпадают по фазе.
),
тогда как колебания напряженности
электрического поля в различных точках
бегущей волны не совпадают по фазе.
Магнитная индукция в данном случае получается из суперпозиции магнитных индукций волн:
 (2.63)
(2.63)
Суммарное поле
отыщется в виде:
![]() (2.64)
(2.64)
Видно, что вектор B также образует стоячую волну, узлы которой совпадают с пучностями стоячей волны E (рис.2.4). По времени колебаний электрического и магнитного полей стоячей ЭМВ отличаются по фазе на четверть периода колебаний. Это означает, что если E достигает максимума, то B = 0, если же E растет, то B уменьшается.
Преобразование
энергии в стоячей волне.
Т.к.
![]() ,
то поток энергии отсутствует в точках,
гдеE =
0 или B
= 0 (H
= 0). Поток энергии через узлы и пучности
в такой волне отсутствует. Поэтому с
течением времени энергия движется между
соседними узлами и пучностями, превращаясь
из энергии магнитного поля в энергию
электрического поля и наоборот, а
пользуясь формулой для объемной плотности
энергии электромагнитного поля
,
то поток энергии отсутствует в точках,
гдеE =
0 или B
= 0 (H
= 0). Поток энергии через узлы и пучности
в такой волне отсутствует. Поэтому с
течением времени энергия движется между
соседними узлами и пучностями, превращаясь
из энергии магнитного поля в энергию
электрического поля и наоборот, а
пользуясь формулой для объемной плотности
энергии электромагнитного поля
![]() (2.65)
(2.65)
можно сказать, что энергия стоячей волны, заключенная между соседними узлами и пучностями, остается постоянной с течением времени.
6 Поляризация электромагнитных волн. Поляризация света – это физическая характеристика оптического излучения, описывающая поперечную анизотропию световых волн, т.е. неэквивалентность различных направлений в плоскости, перпендикулярной направлению распространения волн.
Световые волны, у
которых направления колебаний векторов
электрического ![]() и магнитного
и магнитного ![]() полей сохраняются неизменными в
пространстве или изменяются по
определенному закону называются
поляризованными.
полей сохраняются неизменными в
пространстве или изменяются по
определенному закону называются
поляризованными.
Если вектор ![]() световой волны колеблются лишь в одной
неизменной в пространстве плоскости,
то такая волна называется линейно или
плоско поляризованной. При линейной
поляризации плоскость содержащая
волновой вектор
световой волны колеблются лишь в одной
неизменной в пространстве плоскости,
то такая волна называется линейно или
плоско поляризованной. При линейной
поляризации плоскость содержащая
волновой вектор ![]() и
и ![]() называется плоскость поляризации волны.
называется плоскость поляризации волны.
Если колебания
вектора ![]() совершаются так, что конец описывает
окружность в плоскости, перпендикулярно
направленно распространенной волны
совершаются так, что конец описывает
окружность в плоскости, перпендикулярно
направленно распространенной волны
![]() , то такая волна называется поляризованной
по кругу если эллипс, то эллиптически
поляризованной.
, то такая волна называется поляризованной
по кругу если эллипс, то эллиптически
поляризованной.
Световая волна в
которой различные направления вектора
![]() в поперечной к направлению распространения
волны плоскости равновероятны, называется
естественной ( естественно поляризованной
или неполяризованной).
в поперечной к направлению распространения
волны плоскости равновероятны, называется
естественной ( естественно поляризованной
или неполяризованной).
Закон Малюса
I(![]() )=Iocos2
)=Iocos2![]()
Виды поляризации:
Электронная поляризация - смещение электронного облака относительно центра ядра атома или иона в результате чего возникает электрический момент, исчезающий после окончания действия электрического поля. Наблюдается во всех без исключения диэлектриках. Единственным видом поляризации она является в неполярных диэлектриках.
Ионная поляризация - наблюдается в веществах с ионной химической связью и проявляется в смещении друг относительно друга разноименно заряженных ионов. Как указывалось, время электронной поляризации весьма мало - на 2 - 3 порядка больше ионной поляризации.
Релаксационные (замедленные) виды поляризации - проявляются в газах, жидкостях и твердых диэлектриках в том случае, если они состоят из полярных молекул, диполей или молекул, имеющих отдельные радикалы или части (сегменты), обладающие собственными электрическими моментами:
Ионно – релаксационная поляризация - наблюдается в диэлектриках с ионным типом химических связей, например в неорганических стеклах, имеющих неплотную упаковку ионов, электротехническом фарфоре и других.
Миграционная поляризация наблюдается в неоднородных диэлектриках, имеющих проводящие и полупроводящие включения, слои с различной проводимостью и т.п.
Электронно-релаксационная поляризация характерна для твердых диэлектриков, содержащих дефекты или примесные ионы, способные захватывать электроны.
Спонтанная поляризация
Число независимых поляризаций. Электромагнитная волна с любой поляризацией может быть представлена в идее суперпозиции двух линейно поляризованных волн, плоскости колебаний электрического вектора которых взаимно перпендикулярны.
Рассмотрим такую
суперпозицию с одинаковыми частотами
w,
амплитудами электрических полей ![]() и
и ![]() распространяющихся в одном направлении
( вдоль оси z
декартовой системы координат) со сдвигом
фаз
распространяющихся в одном направлении
( вдоль оси z
декартовой системы координат) со сдвигом
фаз ![]() .
Пусть вектор
.
Пусть вектор ![]() колеблется в плоскости xz,
а вектор
колеблется в плоскости xz,
а вектор ![]() в плоскости yz
в плоскости yz
![]() E1y=E1z=0
E2x=E2z=0
E1y=E1z=0
E2x=E2z=0
![]()
![]()
![]()
![]() - состояние поляризации суммарного
поля в общем виде
- состояние поляризации суммарного
поля в общем виде
