17.Центрированные оптические системы. Параксиальное приближение. Кардинальные элементы оптической системы.

Линзами называют детали из оптически прозрачных однородных материалов ограниченные двумя прямолежащими поверхностями, из которых хоты бы одна яв-ся поверхностью тела вращения(сфера, асферическая или цилиндр.поверхность)

Параксиальное приближение.

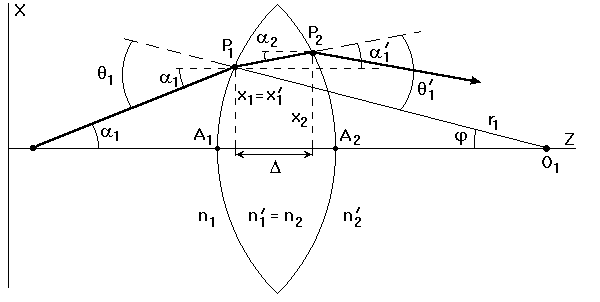
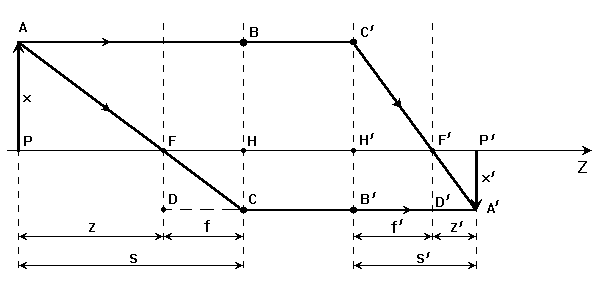
Прохождение лучей в центрированных оптических системах. Рассмотрим прохождение лучей через сферическую линзу, не накладывая ограничений на ее толщину (рис.5.3). Обозначения видны из рисунка.

Ось Z совпадает с осью линзы. Главной оптической осью линзы называется прямая, проходящая через центры кривизны ее поверхности (в данном построении это ось Z). Свет распространяется вдоль положительного направления оси Z. Луч света лежит в плоскости XZ. r₁ и r₂ – радиусы кривизны 1-й и 2-й сферических поверхностей линзы (r₂ на рис.5.3 не показан, чтобы не загромождать рисунок). Весь расчет проводится в параксиальном приближении:

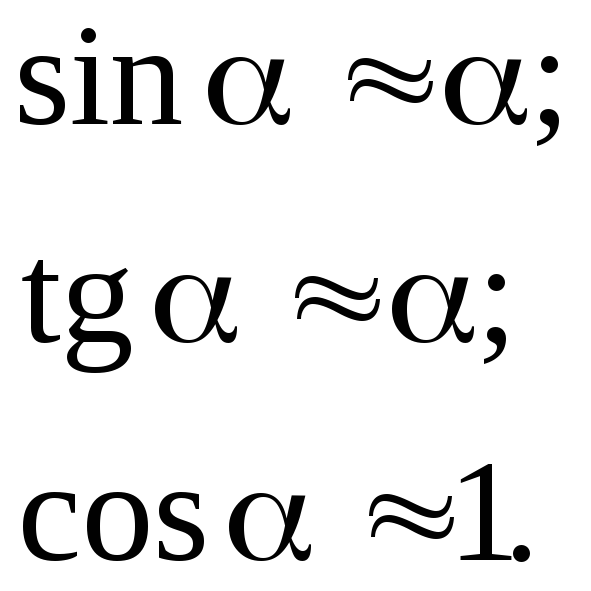
Преломление на первой сферической поверхности. В точке P₁ закон Снеллиуса в параксиальном приближении имеет вид:

Используя геометрические соотношения между углами:(5.24)

а в параксиальном приближенииполучаем:

Кроме этого учтем соотношение(5.27)

Система уравнений (5.26) и (5.27) позволяют, задав координаты падающего на первую поверхность линзы луча (n₁a₁ ; x₁), найти координаты (n₁^/a₁^/ ; x₁^/) преломленного в линзе луча. Полученную систему удобно записать в матричном виде: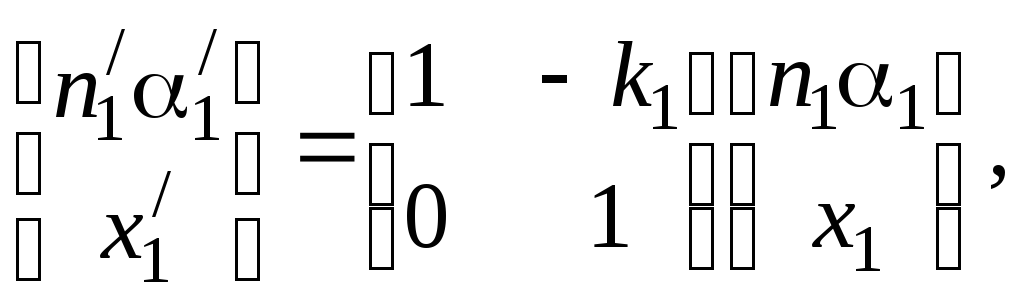где величинаk₁=(n₁^/–n₁)/r₁ называется преломляющей силой первой поверхности, а матрицаназываетсяпреломляющей матрицей первой поверхности.

Распространение луча внутри линзы. Преломленный луч в параксиальном приближении, пройдя внутри линзы, падает на её вторую поверхность на расстоянии x₂ от оси:(5.30)

Отметим, что величина D в параксиальном приближении практически равна толщине линзы А₁А₂ . С учетом, что получаем в матричном виде: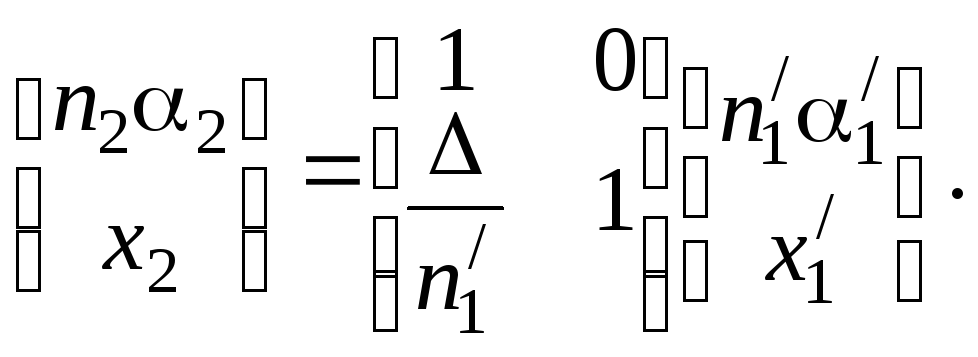

Матрица 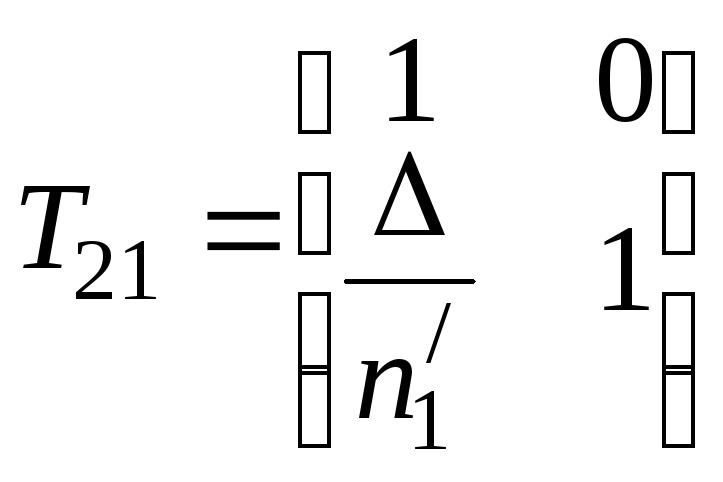(5.32)

описывает распространение луча от первой поверхности линзы ко второй и называется передаточной матрицей.

Преломление луча на второй сферической поверхности рассматривается точно так же, как и на первой поверхности. Величина k₂=(n₂^/ –n₂)/r₂ называется преломляющей силой второй поверхности, а матрица R₂ – преломляющей матрицей второй поверхности:(5.33)

Знаки всех величин в приведенных выражениях необходимо брать с учётом правила знаков: если встречаемая лучом преломляющая поверхность выпуклая, то её радиус кривизны надо брать с положительным знаком, а если вогнутая – с отрицательным; углы a, отсчитываемые от оси Z против часовой стрелки, положительны, а по часовой стрелке – отрицательны; расстояния, отсчитываемые по Z (по рис. 5.3 – слева направо), положительны, а против Z (справа налево) – отрицательны; расстояния от оси Z, отсчитываемые вверх, положительны, вниз – отрицательны.

Распространение луча через оптическую систему. Используя (5.29), (5.31), (5.33), получаем связь между характеристиками на выходе линзы и входе в неё:

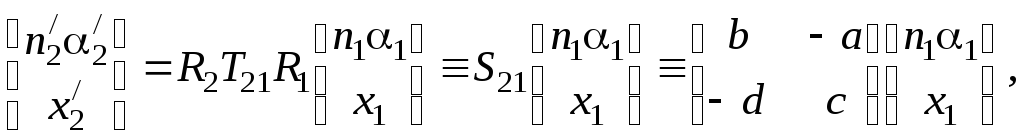(5.34) (5.35)

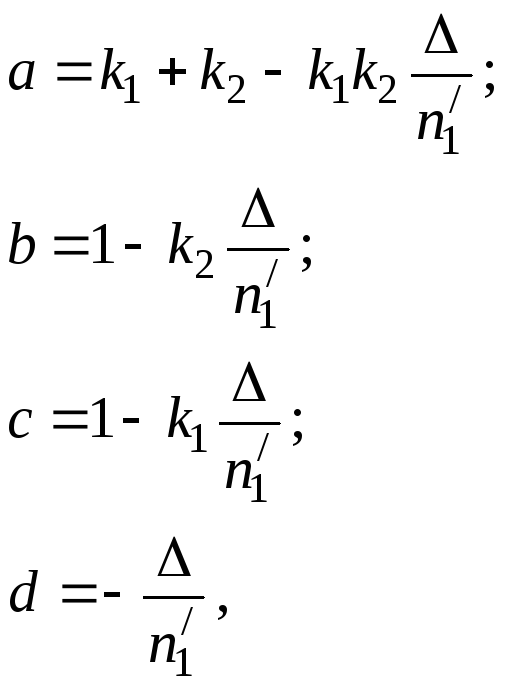(5.36)

где a, b, c, d называются постоянными Гаусса. Независимыми являются только три из четырех постоянных Гаусса. Матрица S₂₁ полностью описывает рассмотренную оптическую систему.

Преобразование луча от плоскости предмета к плоскости изображения. Пусть из точки некоторой плоскости (плоскости предмета), расположенной на расстоянии l слева от точки А₁ выходит луч с координатами (n₁a₁, x) и падает на рассматриваемую линзу. В некоторой плоскости, расположенной справа от точки А₂ на расстоянии l^/ луч характеризуется координатами (n₂^/a₂^/, x^/). Между этими парами координат по приведенным выше правилам получаем соотношение:(5.37)

(Знак l уже учтён)Перемножая матрицы в (5.37), имеем:(5.38)

Матрица Q₂₁ называется матрицей преобразования предмета к изображению:

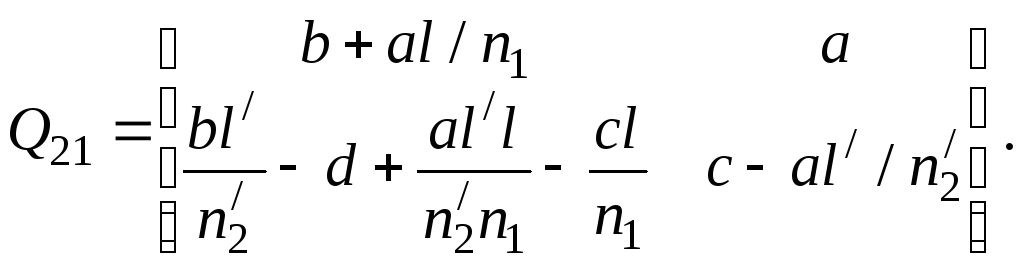(5.39)

Обозначим – увеличение оптической системы.

Изображение- отображение плоскости предмета на плоскость, называемую плоскостью изображения, когда все лучи, исходящие от точки предмета, сходятся после преломления в оптической системе в одной точке плоскости изображения и все точки отображаются с одинаковым увеличением.

Исходя из этого определения в точке изображения увеличение М не должно зависеть от угла a₁. Поэтому соответствующий член в матрице Q₂₁ обращается в нуль:(5.41)

Из определения увеличения и выражения (5.40) имеем:(5.42)

Тогда матрица преобразования от предмета к изображению принимает вид: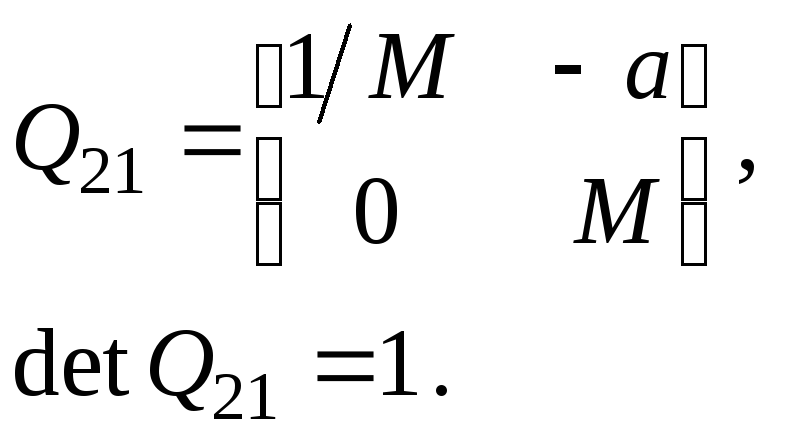(5.43)

Кардинальные элементы оптической системы. Плоскости H и H^/, увеличение для точек которых М = 1, называются главными плоскостями, а их пересечения с осью системы (ось Z) – главными точками системы. Найдём из (5.42) их положение:(5.44)

где l_H – отсчёт положения плоскости H относительно точки А₁; l_H^/ – отсчёт положения плоскости H относительно точки А₂ . Точка на оси системы, в которой сходятся лучи, падающие на оптическую систему параллельно оптической оси (т.е. точка с увеличением M = 0) и точка, выйдя из которой лучи после прохождения оптической системы становятся параллельными оптической оси (т.е. с увеличением M = ¥), называются фокусами оптической системы. Плоскости, проходящие через фокусы перпендикулярно оптической оси, называются фокальными. Найдём из (5.42) их положение:

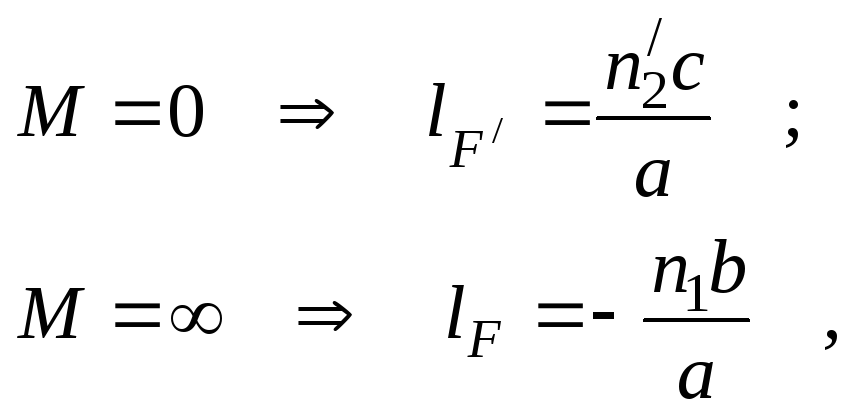
где l_F – отсчёт положения переднего фокуса относительно точки А₁ , l_F^/ – отсчёт положения заднего фокуса относительно точки А₂ Расстояние f между передним фокусом и передней главной точкой называется передним фокусным расстоянием; расстояние f ^/ между задним фокусом и задней главной точкой называется задним фокусным расстоянием:

Главные и фокальные плоскости называются кардинальными элементами оптической системы. Их положение позволяет полностью описать преломление лучей в оптической системе и построить изображение заданного предмета (рис).

Физический смысл постоянных Гаусса. Пусть линза располагается в воздухе: n₁ = n₂^/ = 1. Тогда из (5.46) следует:(5.47)

т.е. a является величиной, обратной фокусному расстоянию. Из (5.45) и (5.47) имеем:

Коэффициенты b и c характеризуют взаимное расположение главных и фокальных плоскостей.