
- •Модуль 20.Магнитное поле
- •20.1. Основные формулы
- •20.2. Примеры решения задач
- •20.3. Контрольные задания
- •22.1. Основные законы
- •22.2. Примеры решения задач
- •22.3. Контрольные задания
- •Модуль 23. Электромагнитные колебания
- •23.1. Основные формулы
- •23.3. Примеры решения задач
- •23.3. Контрольные задания
- •25.1. Основные формулы
- •25.2. Примеры решения задач
- •25.3. Контрольные задания
- •26.1. Основные формулы
- •26.2. Примеры решения задач
- •26.3. Контрольные задания
- •27.1. Основные формулы
- •27.2. Примеры решения задач
- •27.3. Контрольные задания
- •28.1. Основные формулы
- •28.2. Примеры решения задач
- •28.3. Контрольные задания
- •29.1. Основные формулы
- •29.2. Примеры решения задач
- •29.3. Контрольные задания
- •30.1 Основные законы
- •30.2 Примеры решения задач.
- •30.3 Контрольные задания
- •31.1 Основные формулы
- •Для стационарных состояний
- •31.2. Примеры решения задач.
- •31.3 Контрольные задания.
- •32.1. Основные формулы
- •32.3. Контрольные задания.
- •34.1. Основные формулы
- •34.2.Примеры решения задач
- •34.3 Контрольные задания
- •35.1 Основные формулы
- •35.2 Примеры решения задач
- •35.3 Контрольные задания
- •Модуль 36. Атомное ядро
- •36.1 Основные формулы
- •36.2 Примеры решения задач
- •Решение. Дефект массы определяется по формуле
- •36.3 Контрольные задания
- •Основные физические постоянные (округленные значения)
- •Некоторые астрономические величины
25.1. Основные формулы
Законы отражения и преломления света
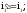
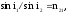
где
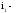 угол
падения;
угол
падения;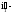 угол
отражения;
угол
отражения; угол
преломления;
угол
преломления;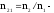 относительный
показатель преломления второй среды
относительно первой;
относительный
показатель преломления второй среды
относительно первой;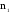 и
и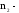 абсолютные
показатели преломления первой и второй
среды.
абсолютные
показатели преломления первой и второй
среды.
Предельный угол полного внутреннего отражения при распространении света из оптически более плотной среды в оптически менее плотную
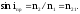
Формула сферического зеркала
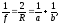
где
а и
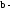 соответственно
расстояния от полюса зеркала до предмета
и изображения;
соответственно
расстояния от полюса зеркала до предмета
и изображения;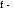 фокусное
расстояние зеркала;
фокусное
расстояние зеркала;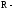 радиус
кривизны зеркала.
радиус
кривизны зеркала.
Оптическая сила тонкой линзы
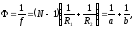
где
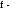 фокусное
расстояние линзы;
фокусное
расстояние линзы;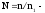 относительный
показатель преломления;
относительный
показатель преломления;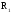 и
и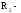 радиусы
кривизны поверхностей (
радиусы
кривизны поверхностей (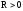 для выпуклой поверхности;
для выпуклой поверхности;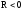 для вогнутой);а
и
для вогнутой);а
и
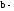 соответственно расстояния от оптического
центра линзы до предмета и изображения.
соответственно расстояния от оптического
центра линзы до предмета и изображения.
Сила света
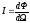 ,
,
где
d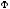 -
световой поток, излучаемый источником
в пределах телесного угла d
-
световой поток, излучаемый источником
в пределах телесного угла d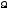 .
.
Полный световой поток, испускаемый изотропным точечным источником
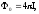
где
 сила света источника.
сила света источника.
Светимость поверхности
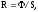
где
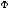 -
световой поток, испускаемый поверхностью;
-
световой поток, испускаемый поверхностью;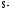 площадь этой поверхности.
площадь этой поверхности.
Яркость
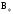 светящейся
поверхности в некотором направлении
светящейся
поверхности в некотором направлении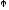
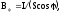
где
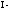 сила
света;
сила
света;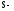 площадь
поверхности;
площадь
поверхности;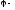 угол
между нормалью к элементу поверхности
и направлением наблюдения.
угол
между нормалью к элементу поверхности
и направлением наблюдения.
Освещенность Е поверхности
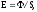
где
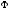 -
световой поток, падающий на поверхность;
-
световой поток, падающий на поверхность;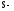 площадь
этой поверхности.
площадь
этой поверхности.
Связь светимости
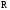 и яркостиВ
при условии, что яркость не зависит от
и яркостиВ
при условии, что яркость не зависит от
направления,
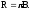
25.2. Примеры решения задач
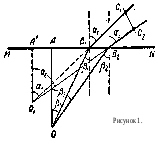
Какова истинная глубина водоема, если при рассматривании дна под углом в 30 кажущаяся глубина его равна 1 м? Показатель преломления воды равен 1,33. (рисунок 25.1).
Дано.
= 30
n = 1,33
h = 1м
H — ?
Решение. Световые лучи ОВ1С1 и ОВ2С2, идущие от точки на дне водоема, прежде чем попасть в глаз наблюдателя, преломляются на поверхности воды MN. Поэтому наблюдателю точка О кажется совмещенной с точкой О1 (точка пересечения продолжения отрезков В1С1 и В2С2).
Из
рисунка 25.1. видно, что с одной стороны
В1В2
=
h
tg2
— h
tg1,
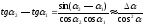
а
с другой
В1В2
=
H
tg2
— H
tg1.
Следовательно,
h(tg2
— tg1)
= H(tg2
— tg1),
откуда,
введем
обозначение: 1
= ,
2
= 1
+ ,
1
= ,
2
=
+
Считая
углы
и
малыми, получим:
Htg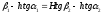 и
следовательно,
и
следовательно,
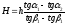 .
По
закону преломления углы
и
связаны друг с другом соотношением:
.
По
закону преломления углы
и
связаны друг с другом соотношением:
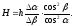
n sin = sin .
Беря от обеих частей последнего равенства полные дифференциалы, мы получим:
n cos d = cos d,
откуда
найдем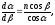
так как = d, = d, то
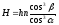
= 30; cos3 = 0,649;
= 22; cos3 = 0,797;
2.
Определить угол отклонения
для луча, проходящего через призму с
преломляющим углом D
= 20,
если луч падает под углом а1
= 5.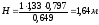
Показатель преломления вещества призмы n = 1,52.
Дано:
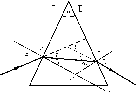
а1 = 5
n = 1,52
—?
Решение.Угол отклонения — это угол между падающим лучом и лучом, выходящим через призму. Выведем приближенную формулу для угла
отклонения. Из рисунка 25.2 следует, Рисунок 25.2
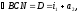
(1)
= 1 + 2 = a1 + i2 — D. (2)
Применим закон преломления4 для грани II:
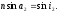
(3)
Из уравнений (1),(2) и (3) находим:
n sin(D — i1) = sin( + D — a).
Разложим
данное выражение в ряд Маклорена,
ограничившись первыми двумя членами:
Dnsini1+nDcosi=—sina1+(D+)cosa1
или
—(+D)cosa1=nsini1—nDcosi1—sina1.
Так
как nsini1=sina1,
то
(4)
Так как угол a1
весьма мал,
то при параксиальных лучах величиной
sin2a1
можно
пренебречь. Тогда выражение (4)
примет вид:
= (n
— 1)
D.
(5)
= 200,52
= 1024.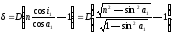
3.Определить смещение луча при прохождении его через плоскопараллельную стеклянную пластинку толщиной 3 см. Показатель преломления стекла 1,755. Угол падения луча равен 45.
Дано:

h = 3 см a1 = 45 d — ?
Решение. Очевидно, что a2 = i1 и i2 = a1
Из рисунка 25.3 видно, что смещение луча d равно
d = AB sin(i2 — a2), Рисунок 25.3
Следовательно,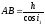
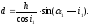
Угол
 1
= 45,
а угол i1
определим из соотношения sin
1
= 45,
а угол i1
определим из соотношения sin 1
= n
sini1:
1
= n
sini1:
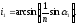
i 24; d 1,1 см.
