32.1. Основные формулы

Коэффициент прозрачности 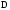прямоугольного потенциального барьера

конечной ширины

где множитель, который можно приравнять к единице;высота потенциального барьера;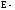энергия частицы.

 Одномерное уравнение Шредингера для стационарных состояний

,

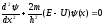где - волновая функция, описывающая состояние частицы;- масса частицы; Е- полная энергия;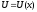- потенциальная энергия частицы.

 Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика:

а) 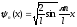(собственная нормированная волновая функция);

б) 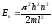(собственное значения энергии),

где - квантовое число (=1,2,3,…);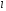- ширина ящика. В области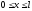и

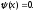
1. Примеры решения задач

1. Волновая функция 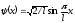описывает основное состояние частицы в бесконечно глубо­ком прямоугольном ящике шириной. Вычислить вероят­ность нахождения частицы в малом интервале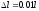в двух случаях: 1 (вблизи стенки) (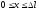); 2) в средней части ящика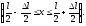

Решение. Вероятность того, что частица будет обнаружена в интервале dx (от х до х + dx), пропорциональна этому интервалу, и квадрату модуля волновой функции, описывающей данное состояние, равна

В первом случае искомая вероятность найдется интегрированием в пределах от 0 до 0,01(рис. 64):

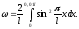
Знак модуля опущен, так как 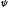— функция в данном случае не является комплексной.

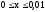
Так как х изменяется в интервале 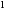и, следовательно, справедливо приближенное равенство

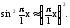
С учетом этого выражения (1) примет вид

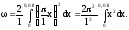
После интегрирования получим

Во втором случае можно обойтись без интегрирования, так как квадрат модуля волновой функции вблизи ее максимума в заданном малом интервале (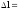0,01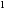) практически не изменяется. Искомая вероятность во втором случае определяется выражением

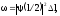
или

32.3. Контрольные задания.

32.1. Написать уравнение Шредингера для линейного гармонического осциллятора.Учесть, что сила, возвращающая частицу в положение равновесия,  = - кх (где к – коэффициент пропорциональности, х - смещение).

32.2. Временная часть уравнения Шредингера имеет вид . Найти решение уравнения.

32.3.Написать уравнение Шредингера для свободного электрона, движущегося в положительном направлении оси Х со скоростью . Найти решение этого уравнения.

32.4. Электрон находится в бесконечно глубоком прямоугольном одномерном потенциальном ящике шириной 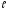. Написать уравнение Шредингера и его решение ( в тригонометрической форме).

32.5.Электрону в потенциальном ящике шириной отвечает волновое число к=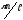( n = 1,2,3,…). Используя связь энергии Е электрона с волновым числом к, получить выражения для собственных значений Е_n.

32.6. Частица находится в потенциальном ящике. Найти отношение разности соседних энергетических уровней 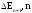к энергии частицы Е_n при n  . Пояснить полученные результаты.

32.7.Электрон находится в потенциальном ящике шириной 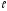= 0,5 нм. Опередить наименьшую разность энергетических уровней электрона. Ответ выразить в электрон – вольтах.

32.8. Электрон находится в одномерном потенциальном ящике шириной 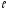. Определить среднее значение координаты х  электрона ( 0  х  ).

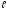32.9. Частица находится в бесконечно глубоком, одно­мерном, прямоугольном потенциальном ящике. Найти отношение разности 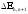соседних энергетических уровней к энергиичастицы в трех случаях: 1).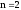; 2)= 5; 3).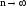

32.10. В прямоугольной потенциальной яме шириной 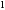с абсолютно непроницаемыми стенками (0 <х < 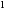) на­ходится частица в основном состоянии. Найти вероят­ностьместонахождения этой частицы в области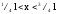

Модуль 34. Конденсированное состояние

Элементы структурной кристаллографии. Методы исследования кристаллических структур. Теп­лоемкость кристаллической решетки. Фоновый газ. Размерный эффект в теплопроводности кристаллов. Носители тока как квазичастицы. Энерге­тические зоны в кристаллах. Уровень Ферми. Поверхность Ферми. Метал­лы, диэлектрики и полупроводники в зонной теории. Понятие дырочной проводимости. Собственная и примесная проводимость. Явление сверх­проводимости. Куперовское спаривание. Кулоновское отталкивание и фононное притяжение. Эффект Джозефсона. Квантовые представления о свойствах ферромагнетиков. Обменное взаимодействие. Температура Кю­ри. Намагничивание ферромагнетиков.