
- •Казахский Национальный Технический УниверситетИм.К.И. Сатпаева
- •Содержание
- •2. Конспект лекционных занятий
- •1. При установившейся фильтрации капельной жидкости можно считать ее плотность независящей от давления, т.Е. Рассматривать жидкость как несжимаемую. Тогда,
- •Лекция № 10. Обобщение расчетных формул на случай слоисто-неоднородных и зонально-неоднородных пластов
- •Лекция № 13. Приток жидкости к гидродинамически несовершенным скважинам
- •Лекция № 18. Неустановившееся движение упругой жидкости в пористой среде
- •Лекция № 19. Прямолинейно-параллельный неустановившийся поток упругой жидкости
- •Лекция № 21,22. Приближенные методы решения задач теории упругого режима
- •Лекция № 24. Решение задачи о притоке газа к скважине методом пссс.
- •Лекция № 25. Приближенное решение задач об отборе газа из замкнутого пласта.
- •Лекции № 26, 27. Взаимное вытеснение жидкостей
- •Лекция № 28. Двухфазное течение несмешивающихся жидкостей. Теория Баклея-Леверетта
- •Лекция № 29, 30. Особенности фильтрации в трещиноватых и трещиновато-пористых пластах
- •ГлоссариЙ
- •Литература
Лекция № 21,22. Приближенные методы решения задач теории упругого режима
Метод ПССС.
Плоско-параллельный поток.
А. В момент времени t=0
в горизонтальном пласте постоянной
толщиныhи шириныBпущена в эксплуатацию галерея с постоянным
забойным давлением. До пуска галереи
во всем пласте![]() .
.
Требуется найти распределение давления, закон перемещения границы возмущенной области l(t)и изменение дебита галереи во времениQ(t).
Дебит галереи при установившемся процессе
![]() (1)
(1)
Воспользуемся уравнением материального баланса
![]() (2)
(2)
где
![]()
![]()
![]() ,
(3)
,
(3)
Подставляя (1) в (2) с учетом (3), получим
![]()
![]()
![]() (4)
(4)
После интегрирования (4) будем иметь:
![]() или
или![]() (5)
(5)
Распределение давления в возмущенной зоне
![]() (6)
(6)
с учетом (5) имеем
![]()
![]() (7)
(7)
Дебит галереи
![]() ,
,
![]()
![]() (8)
(8)
Погрешность не превосходит 11%
B, в том же пласте, как и в случае А, пущена галерея с постоянным дебитом.
В этом случае уравнения (2) с учетом (1) принимает вид:
![]() (9)
(9)
или
![]()
![]()
интегрируя
![]() ,
получим,
,
получим,
![]() откуда
откуда![]() (10)
(10)
Распределение давления из (6) с учетом (1)
![]()
![]() ,
,
![]()
![]() (11)
(11)
значение
![]() определяется из (11) при х=
определяется из (11) при х=
![]() (12)
(12)
погрешность до 25%.
Плоскорадиальный поток
Пусть в неограниченном горизонтальном
пласте постоянной толщины hв момент времениt=0,
пущена добывающая скважина радиусаr![]() с
постоянным дебитомQ.
До пуска скважины во всем пласте
с
постоянным дебитомQ.
До пуска скважины во всем пласте![]() .
.
Через время tпосле пуска скважины вокруг нее образуется возмущенная область радиусаr где давление в соответствии с ПССС будет распределяться по стационарному закону
![]() (13)
(13)
Дебит скважины
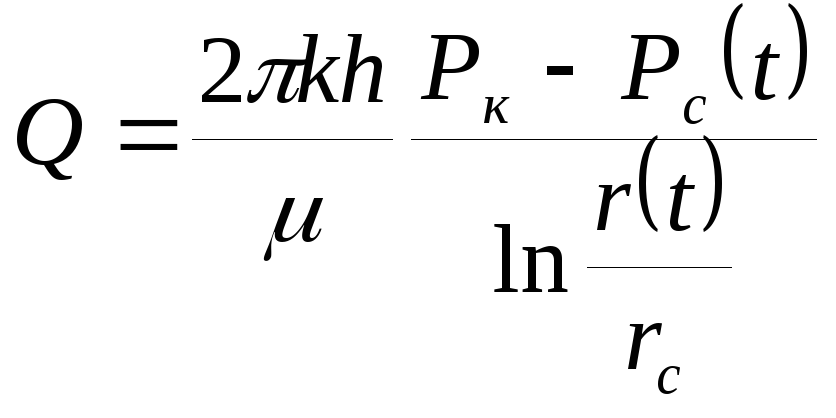 (14)
(14)
Размеры возмущенной области
![]() (15)
(15)
Т. к.
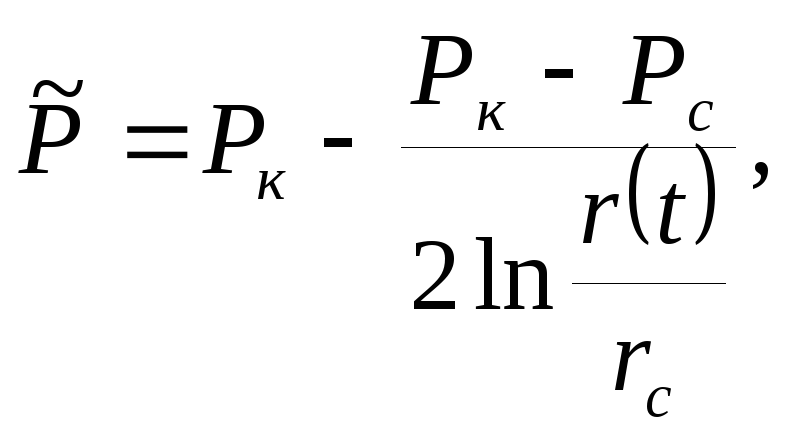 то
то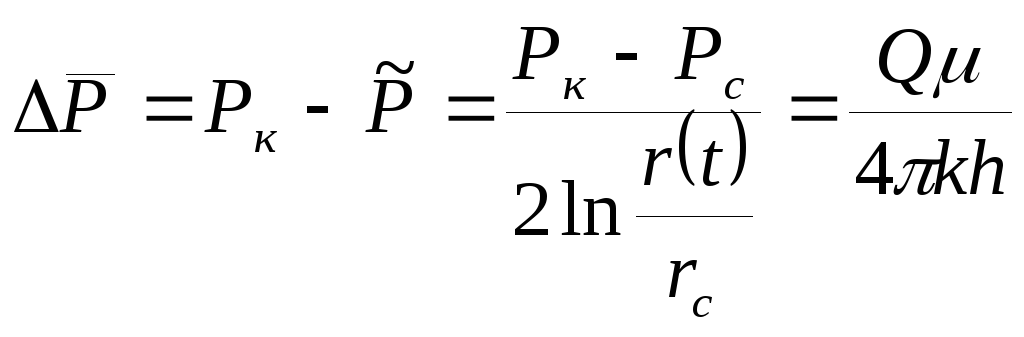 (16)
(16)
Подставив (15) и (16) в уравнение материального баланса (2), получим
![]()
или
![]()
откуда
![]() (17)
(17)
Подставляя (17) в (13), будем иметь
![]()
![]()
![]()
![]() (18)
(18)
Давление на скважине определяют из (8) при r=rc:
![]() (19)
(19)
погрешность 10%.
2. Метод А. М. Пирвердяна.
В отличие от ПССС распределение давления в возмущенной области по методу А.М. Пирвердяна задается в виде квадратной параболы.
Рассматривается плоско-параллельный неустановившийся поток упругой жидкости.
А. Рассмотрим случай постоянного дебита Q=const.
Уравнение распределения давления в возмущенной области
![]() (20)
(20)
Дебит галереи
![]() (21)
(21)
Градиент давления из (20)
![]()
тогда (22)
Средневзвешенное по объему пластовое давление
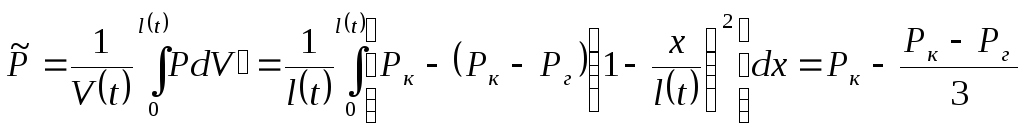
тогда
![]() (23)
(23)
Уравнение материального баланса примет
вид:
![]()
откуда
![]() (24)
(24)
Интегрируя (24) в пределах от 0до tи от0доlполучим
![]() (25)
(25)
Распределение давления в возмущенной области
![]() ,0 < x
,0 < x![]() ,
,
![]()
![]()
![]()
Давление на галерее определяется при
![]() (26)
(26)
погрешность 9%, т. е. в 2,5 раза меньше, чем при
B. Рассмотрим случай,
когда![]() .
.
Уравнение материального баланса в этом случае принимает вид (с учетом (22) и (23))
![]()
или
![]() откуда
откуда![]() (27)
(27)
Распределение давления в возмущенной области:
![]() (28)
(28)
Дебит галереи
![]() (29) погрешность около 2,5 %.
(29) погрешность около 2,5 %.
Основная литература:2 [151-162]
Контрольные вопросы:
Сущность метода ПССС.
Закон перемещения внешней границы возмущенной области при постоянном дебите.
Закон перемещения внешней границы возмущенной области при Рг =const.
Сущность метода А.М. Пирвердяна.
Закон перемещения внешней границы возмущенной области по методу А.М. Пирвердяна.
Лекция № 23. Неустановившееся движение газа в пористой среде
Для вывода дифференциального уравнения неустановившейся фильтрации идеального газа в уравнении неразрывности потока подставляются выражения для компонента скорости фильтрации и уравнения состояния идеального газа.
Считая коэффициенты пористости m![]() ,
проницаемости k
и вязкости газа
,
проницаемости k
и вязкости газа![]() постоянными
получим
постоянными
получим
![]() ,
(1)
,
(1)
где
![]()
Рассмотрим конкретную задачу о притоке газа в скважину, расположенную в пласте бесконечной протяженности с постоянной толщиной h.
Дифференциальное уравнение (1) в данном случае имеет вид:
![]() (2)
(2)
которое решается при начальном и граничном условиях:
![]() приt=0
приt=0
![]() при
при![]() 0(3)
0(3)
Введем условие на забое скважины - Q![]() =constмассовый дебит.
=constмассовый дебит.
Q![]()
![]()
Откуда![]() (4)
(4)
Проводя аналогию между неустановившейся
фильтрацией упругой жидкости и идеального
газа делаем вывод, что все соотношения
для идеального газа давление входит в
квадрате, коэффициент пьезопроводности
для жидкости
![]() заменяется
на
заменяется
на![]() для газа, коэффициент
для газа, коэффициент![]() В
остальном все соотношения аналогичны.
В
остальном все соотношения аналогичны.
Тогда решение уравнения (2) при условии (3) и (4) имеет вид
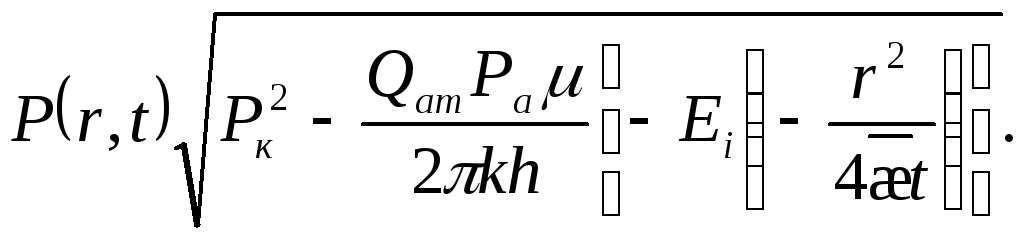 (5)
(5)
Изменим давление на забое скважины (при r=rc)
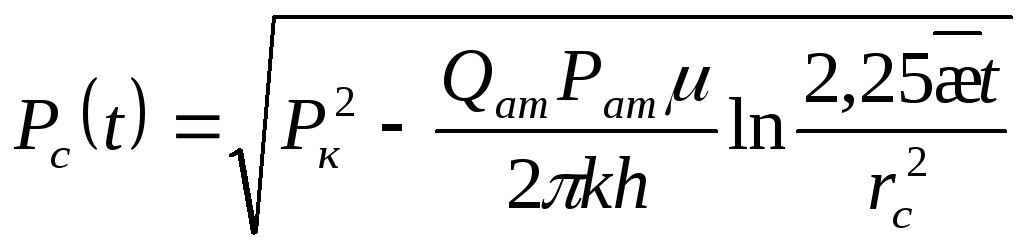 (6)
(6)
Основная литература:2 [170-184]
Дополнительная литература:4 [303-310]
Контрольные вопросы:
Дифференциальное уравнение фильтрации газа.
Аналогия между неустановившейся фильтрацией упругой жидкости и идеального газа.
Определение давления на стенке газовой скважины при постоянном дебите.
