
- •1.Числовая последовательности и ее предел.
- •2.Способы задания функции.
- •1. Аналитический способ
- •2. Табличный способ
- •3. Графический способ
- •3.Предел функции. Односторонние пределы.
- •Левый и правый пределы функции
- •4.Первый замечательный предел.
- •7.Производная. Геометрический и механический смысл производной
- •8.Таблица производных и правила дифференцирования
- •9.Возрастание и убывание функции
- •Точки экстремума, экстремумы функции.
- •Достаточные условия возрастания и убывания функции.
- •Достаточные условия экстремума функции.
- •Первое достаточное условие экстремума.
- •Второй признак экстремума функции.
- •Третье достаточное условие экстремума функции.
- •10. Экстремумы функции Определение экстремума
- •Точки экстремума
- •Задачи на нахождения экстремума функции
- •11.Производные высших порядков. Формула Тейлора
- •Формула Тейлора
- •Определённый интеграл
- •13. Геометрический смысл определенного интеграла.
- •14.Определение числового ряда. Сходимость ряда.
- •15.Признак сходимости Даламбера и Коши
- •17.Понятие суммы степенного ряда. Ряд Тейлора
- •Определение
- •Формула Тейлора для большого числа переменных
- •19.Частная производная
- •Обозначение
- •Геометрическая интерпретация
- •Примеры
- •21.Дифференциальное уравнение
- •Обыкновенные дифференциальные уравнения
- •Порядок дифференциального уравнения
- •Простейшие дифференциальные уравнения первого порядка
- •Дифференциальные уравнения в частных производных
- •Линейные и нелинейные дифференциальные уравнения
- •Примеры
11.Производные высших порядков. Формула Тейлора
Если
функция ![]() имеет
производную в каждой точке
имеет
производную в каждой точке ![]() своей
области определения, то ее производная
своей
области определения, то ее производная ![]() есть
функция от
есть
функция от ![]() .
Функция
.
Функция ![]() ,
в свою очередь, может иметь производную,
которую называют производной
второго порядка функции
,
в свою очередь, может иметь производную,
которую называют производной
второго порядка функции ![]() (или второй
производной)
и обозначают символом
(или второй
производной)
и обозначают символом ![]() .
Таким образом
.
Таким образом
![]()
Пример
Задание. Найти
вторую производную функции ![]()
Решение. Для начала найдем первую производную:
![]()
![]()
![]()
![]()
Для нахождения второй производной продифференцируем выражение для первой производной еще раз:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ. ![]()
Больше примеров решенийРешение производных онлайн
Производные
более высоких порядков определяются
аналогично. То есть производная ![]() -го
порядка функции
-го
порядка функции ![]() есть
первая производная от производной
есть
первая производная от производной ![]() -го
порядка этой функции:
-го
порядка этой функции:
![]()
Формула Тейлора
Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.
Формула Тейлора
![]()
, где Rn(x) - остаточный член формулы Тейлора.
Остаточный член формулы Тейлора
В форме Лагранжа:
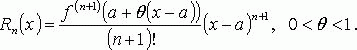
В форме Коши:
![]()
12.Неопределенный и определенный интегралы
Неопределённый интеграл.
![]() Определение.
Функция F(x) называется первообразной
для функции f(x) на интервале X=(a,b) (конечном
или бесконечном), если в каждой точке
этого интервала f(x) является производной
дляF(x), т.е.
Определение.
Функция F(x) называется первообразной
для функции f(x) на интервале X=(a,b) (конечном
или бесконечном), если в каждой точке
этого интервала f(x) является производной
дляF(x), т.е. ![]() .
.
![]() Из
этого определения следует, что задача
нахождения первообразной обратна задаче
дифференцирования: по заданной функции
f(x ) требуется найти функцию F(x), производная
которой равна f(x).
Из
этого определения следует, что задача
нахождения первообразной обратна задаче
дифференцирования: по заданной функции
f(x ) требуется найти функцию F(x), производная
которой равна f(x).
![]() Первообразная
определена неоднозначно: для
функции
Первообразная
определена неоднозначно: для
функции ![]() первообразными
будут и функция arctg x, и функция arctg
x-10:
первообразными
будут и функция arctg x, и функция arctg
x-10: ![]() .
Для того, чтобы описать все множество
первообразных функции f(x), рассмотрим
.
Для того, чтобы описать все множество
первообразных функции f(x), рассмотрим
![]() Свойства
первообразной.
Свойства
первообразной.
Если функция F(x) - первообразная для функции f(x) на интервале X, то функция f(x) + C, где C - произвольная постоянная, тоже будет первообразной для f(x) на этом интервале. (Док-во:
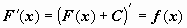 ).
).Если функция F(x) - некоторая первообразная для функции f(x) на интервале X=(a,b), то любая другая первообразная F1(x) может быть представлена в виде F1(x) = F(x) + C, где C - постоянная на X функция.
![]() Из
этих свойств следует, что если F(x) -
некоторая первообразная функции f(x) на
интервале X, то всё множество первообразных
функции f(x) (т.е. функций, имеющих
производную f(x) и дифференциал f(x) dx) на
этом интервале описывается выражением
F(x) + C, где C - произвольная постоянная.
Из
этих свойств следует, что если F(x) -
некоторая первообразная функции f(x) на
интервале X, то всё множество первообразных
функции f(x) (т.е. функций, имеющих
производную f(x) и дифференциал f(x) dx) на
этом интервале описывается выражением
F(x) + C, где C - произвольная постоянная.
Неопределённый
интеграл и его свойства.
![]() Определение.
Множество первообразных функции f(x)
называется неопределённым интегралом
от этой функции и обозначается
символом
Определение.
Множество первообразных функции f(x)
называется неопределённым интегралом
от этой функции и обозначается
символом ![]() .
.
![]() Как
следует из изложенного выше, если F(x) -
некоторая первообразная функции f(x),
то
Как
следует из изложенного выше, если F(x) -
некоторая первообразная функции f(x),
то ![]() ,
где C - произвольная постоянная. Функцию
f(x) принято называть подынтегральной
функцией, произведение f(x) dx - подынтегральным
выражением.
,
где C - произвольная постоянная. Функцию
f(x) принято называть подынтегральной
функцией, произведение f(x) dx - подынтегральным
выражением.
![]() Свойства
неопределённого интеграла, непосредственно
следующие из определения:
Свойства
неопределённого интеграла, непосредственно
следующие из определения:
 .
. (или
(или 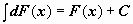 ).
).
Таблица неопределённых интегралов.
|
1 |
|
11 |
|
|
2 |
|
12 |
|
|
3 |
|
13 |
|
|
4 |
|
14 |
|
|
5 |
|
15 |
|
|
6 |
|
16 |
|
|
7 |
|
17 |
|
|
8 |
|
18 |
|
|
9 |
|
19 |
|
|
10 |
|
20 |
|
В
формулах 14, 15, 16, 19 предполагается, что
a>0. Каждая из формул таблицы справедлива
на любом интервале, на котором непрерывна
подынтегральная функция. Все эти формулы
можно доказать дифференцированием
правой части. Докажем, например, формулу
4: если x > 0, то ![]() ;
если x < 0, то
;
если x < 0, то ![]() .
Простейшие
правила интегрирования.
.
Простейшие
правила интегрирования.
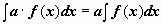 (
( )
)
