Второй признак экстремума функции.

Пусть ,

• если , то - точка минимума;

• если , то - точка максимума.

Как видите, этот признак экстремума функции требует существования производной как минимум до второго порядка в точке .

Пример.

Найти экстремумы функции .

Решение.

Начнем с области определения:

Продифференцируем исходную функцию:

Производная обращается в ноль при x=1, то есть, это точка возможного экстремума. Находим вторую производную функции и вычисляем ее значение при x = 1:

Следовательно, по второму достаточному условию экстремума, x=1 - точка максимума. Тогда 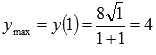- максимум функции.

Графическая иллюстрация.

Ответ:

Третье достаточное условие экстремума функции.

Пусть функция y=f(x) имеет производные до n-ого порядка в -окрестности точки и производные до n+1-ого порядка в самой точке . Пусть и .

Тогда,

• если n – четное, то - точка перегиба;

• если n – нечетное, то - точка экстремума, причем

  • если , то - точка минимума;

  • если , то - точка максимума.

Пример.

Найти точки экстремума функции .

Решение.

Исходная функция является целой рациональной, ее областью определения является все множество действительных чисел.

Продифференцируем функцию:

Производная обращается в ноль при , следовательно, это точки возможного экстремума. Воспользуемся третьим достаточным условием экстремума.

Находим вторую производную и вычисляем ее значение в точках возможного экстремума (промежуточные вычисления опустим):

Следовательно, - точка максимума (для третьего достаточного признака экстремума имеем n=1 и ).

Для выяснения характера точек находим третью производную и вычисляем ее значение в этих точках:

Следовательно, - точка перегиба функции (n=2 и ).

Осталось разобраться с точкой . Находим четвертую производную и вычисляем ее значение в этой точке:

Следовательно, - точка минимума функции.

Графическая иллюстрация.

Ответ:

 - точка максимума, - точка минимума функции.

10. Экстремумы функции Определение экстремума

Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x₁< x₂ выполняется неравенство (f(x₁) < f (x₂) (f(x₁) > f(x₂)).

Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f ^'(x)  0

(f ^' (x)  0).

Точка x_о называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки x_о, для всех точек которой верно неравенство f(x) ≤ f(x_о) (f(x) ≥ f(x_о)).

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.

Точки экстремума

Необходимые условия экстремума. Если точка x_о является точкой экстремума функции f(x), то либо f ^'(x_о) = 0, либо f (x_о) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x_о - критическая точка. Если f ^' (x) при переходе через точку x_о меняет знак плюс на минус, то в точке x_о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x_о экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную  f ^' (x) в окрестности точки x_о и вторую производную  в самой точке x_о. Если f ^' (x_о) = 0, >0 (<0), то точка x_о является точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

Пример 3.22. Найти экстремумы функции f(x) = 2x³ - 15x²+ 36x - 14.

Решение. Так как f ^'(x) = 6x² - 30x +36 = 6(x -2)(x - 3), то критические точки функции x₁ = 2 и x₂ = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x₁ = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x₂ = 3 производная меняет знак минус на плюс, поэтому в точке x₂ = 3 у функции минимум. Вычислив значения функции в точках x₁ = 2 и x₂ = 3, найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) = 13.