Примеры
—
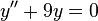однородное
дифференциальное уравнение второго
порядка с постоянными коэффициентами.
Решением является семейство функций 
,
где 
и 
—
произвольные константы, которые для
конкретного решения определяются из
задаваемых отдельно начальных условий.
Это уравнение, в частности, описывает
движение гармонического осциллятора
с циклической частотой 3.
Второй закон Ньютона можно записать в форме дифференциального уравнения
где m —
масса тела, x —
его координата, F(x, t) —
сила, действующая на тело с координатой x в
момент времени t.
Его решением является траектория
движения тела под действием указанной
силы.
Дифференциальное уравнение Бесселя — обыкновенное линейное однородное уравнение второго порядка с переменными коэффициентами:
Его
решениями являются функции
Бесселя.
Пример неоднородного нелинейного обыкновенного дифференциального уравнения 1-го порядка:
В следующей группе примеров неизвестная функция u зависит от двух переменных x и t или x и y.
Однородное линейное дифференциальное уравнение в частных производных первого порядка:
Одномерное волновое уравнение — однородное линейное уравнение в частных производных гиперболического типа второго порядка с постоянными коэффициентами, описывает колебание струны, если
—
отклонение струны в точке с координатой x в
момент времени t,
а параметр a задаёт
свойства струны:
Уравнение Лапласа в двумерном пространстве — однородное линейное дифференциальное уравнение в частных производных второго порядка эллиптического типа с постоянными коэффициентами, возникающее во многих физических задачах механики, теплопроводности, электростатики, гидравлики:
Уравнение Кортевега — де Фриза, нелинейное дифференциальное уравнение в частных производных третьего порядка, описывающее стационарные нелинейные волны, в том числе солитоны:
