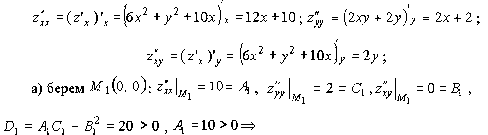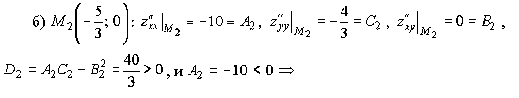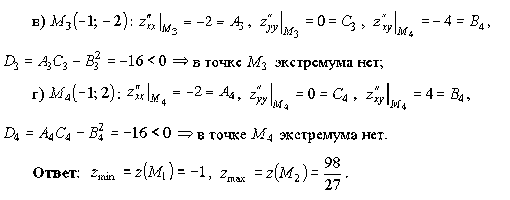- •1.Числовая последовательности и ее предел.
- •2.Способы задания функции.
- •1. Аналитический способ
- •2. Табличный способ
- •3. Графический способ
- •3.Предел функции. Односторонние пределы.
- •Левый и правый пределы функции
- •4.Первый замечательный предел.
- •7.Производная. Геометрический и механический смысл производной
- •8.Таблица производных и правила дифференцирования
- •9.Возрастание и убывание функции
- •Точки экстремума, экстремумы функции.
- •Достаточные условия возрастания и убывания функции.
- •Достаточные условия экстремума функции.
- •Первое достаточное условие экстремума.
- •Второй признак экстремума функции.
- •Третье достаточное условие экстремума функции.
- •10. Экстремумы функции Определение экстремума
- •Точки экстремума
- •Задачи на нахождения экстремума функции
- •11.Производные высших порядков. Формула Тейлора
- •Формула Тейлора
- •Определённый интеграл
- •13. Геометрический смысл определенного интеграла.
- •14.Определение числового ряда. Сходимость ряда.
- •15.Признак сходимости Даламбера и Коши
- •17.Понятие суммы степенного ряда. Ряд Тейлора
- •Определение
- •Формула Тейлора для большого числа переменных
- •19.Частная производная
- •Обозначение
- •Геометрическая интерпретация
- •Примеры
- •21.Дифференциальное уравнение
- •Обыкновенные дифференциальные уравнения
- •Порядок дифференциального уравнения
- •Простейшие дифференциальные уравнения первого порядка
- •Дифференциальные уравнения в частных производных
- •Линейные и нелинейные дифференциальные уравнения
- •Примеры
19.Частная производная
В математическом анализе частная производная — одно из обобщений понятия производной на случай функции нескольких переменных. Частная производная — это предел отношения приращения функции по выбранной переменной к приращению этой переменной, при стремлении этого приращения к нулю.
В
явном виде частная производная функции ![]() в
точке
в
точке ![]() определяется
следующим образом:
определяется
следующим образом:
![]()
Обозначение
Следует
обратить внимание, что обозначение ![]() следует
понимать как цельный символ,
в отличие от обычной производной функции
одной переменной
следует
понимать как цельный символ,
в отличие от обычной производной функции
одной переменной ![]() , которую
можно представить, как отношение
дифференциалов функции и аргумента.
Однако, и частную производную можно
представить как отношение дифференциалов,
но в этом случае необходимо обязательно
указывать, по какой переменной
осуществляется приращение функции:
, которую
можно представить, как отношение
дифференциалов функции и аргумента.
Однако, и частную производную можно
представить как отношение дифференциалов,
но в этом случае необходимо обязательно
указывать, по какой переменной
осуществляется приращение функции: ![]() ,
где
,
где ![]() — частный
дифференциал функции
— частный
дифференциал функции ![]() по
переменной
по
переменной ![]() .
Часто непонимание факта цельности
символа
.
Часто непонимание факта цельности
символа ![]() является
причиной ошибок и недоразумений, как,
например, сокращение
является
причиной ошибок и недоразумений, как,
например, сокращение ![]() в
выражении
в
выражении ![]() . [1].
. [1].
Геометрическая интерпретация
Геометрически,
частная производная является производной
по направлению одной
из координатных осей. Частная производная
функции ![]() в
точке
в
точке ![]() по
координате
по
координате ![]() равна
производной
равна
производной ![]() по
направлению
по
направлению ![]() ,
где единица стоит на
,
где единица стоит на ![]() -ом
месте.
-ом
месте.
Примеры

Объём конуса зависит от высоты и радиуса основания
Объём V конуса зависит от высоты h и радиуса r, согласно формуле
![]()
Частная производная объема V относительно радиуса r
![]()
которая
показывает скорость,
с которой изменяется объём конуса, если
его радиус меняется, а его высота остаётся
неизменной. Например, если считать
единицы измерения объёма ![]() ,
а измерения длины
,
а измерения длины ![]() ,
то вышеуказанная производная будет
иметь размерность скорости измерения
объёма
,
то вышеуказанная производная будет
иметь размерность скорости измерения
объёма ![]() ,
т.е. изменение величины радиуса на 1 м
будет соответствовать изменению объёма
конуса на
,
т.е. изменение величины радиуса на 1 м
будет соответствовать изменению объёма
конуса на ![]()
![]() .
.
Частная производная относительно h
![]()
которая показывает скорость, с которой изменяется объём конуса, если его высота меняется, а его радиус остаётся неизменным.
Полная производная V относительно r и h

и

Различие между полной и частной производной — устранение косвенных зависимостей между переменными в последней.
Если (по некоторым причинам) пропорции конуса остаются неизменными, то высота и радиус находятся в фиксированном отношении k,
![]()
Это даёт полную производную относительно r:
![]()
|
20. Экстремум функции двух переменных | |
|