2. Практическая часть

В практической части будут рассмотрены 3 различные реализации преобразователя Гильберта, каждая со своими особенностями:

В пункте 2.1 будет рассмотрен фильтр, сформированный по формуле (1.4), реализация модели которого будет производиться на языке программирования С++.

В пункте 2.2 будет рассмотрен фильтр, сформированный по методу Паркса-Макклеллана в среде MatLab с помощью функции remez.

В пункте 2.4 оператор ДПГ будет сформирован по формуле (1.4) и затем оцифрован (дискретизирован по уровню) в среде ModelSim, на языке описания аппаратурыVerilog.

2.1 Реализация модели преобразователя на языке программирования C++

Пишем программу, состояющию из 3х блоков. Главный блок, в котором формируем оператор дискретного преобразования Гильберта, исходный сигнал, также в этом блоке будут использованы 2 других блока, один из которых отвечает за дискретную свёртку исходного сигнала с оператором дискретного преобразования Гильберта, а другой за округление отсчётов оператора дискретного преобразования Гильберта, чтобы чётные отсчёты были равно абсолютному нулю. Все результаты записываются в текстовые файлы, с помощью которых с помощью среды MatLabя построю графики.

Рассмотрим подробней параметры сигнала и преобразователя Гильберта.

Исходный дискретизированный по времени сигнал y:

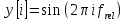
, где i– отсчёты,f_rel– относительная частота, определяется как:

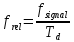
, где f_signal– частота сигнала,T_d – период дискретизации сигнала.

В нашем случае f_rel= 1, что соответствует 4 отсчётам на период синуса.

Затем формируем оператор дискретного преобразования Гильберта по выведенной ранее в теоретической части формуле, при этом выполняя условия каузальности : отклик не может опережать воздействие, поэтому задерживаем оператор дискретного преобразования на (N-1)/2, гдеN– нечётное количество отсчётов оператора.

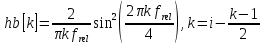
На рисунке 2.1.1 представлен полученный оператор дискретного преобразования.

Затем с помощью свёртки последовательностей находим свёртку исходного сигнала и оператора дискретного преобразования Гильберта. Результат показан на рисунке 2.1.2. Для того, чтобы убедиться что все операции проведены правильно, сравним полученный сигнал с отрицательным задержанным косинусом (см. теоретическую часть) на той же частоте, что и исходный синус. Задержка при сравнении необходима потому, что преобразование Гильберта само по себе задерживает полученный сигнал относительно исходного. В правильности проделанных операций можем убедиться на рисунке 2.1.3.

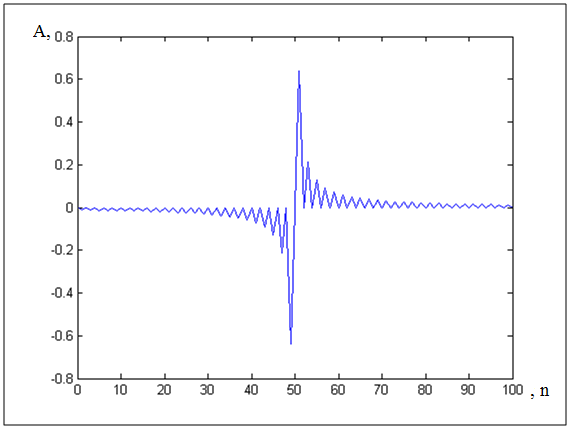
Рисунок 2.1.1 - Оператор дискретного преобразования Гильберта

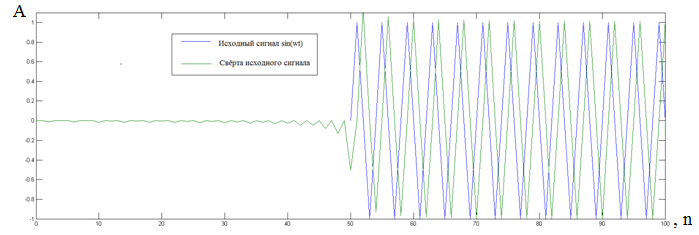
Рисунок 2.1.2 - Исходный сигнал и его свёртка

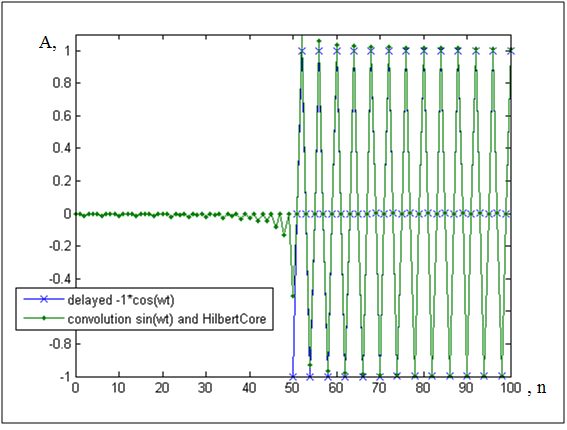
Рисунок 2.1.3 - Задержанный сигнал -cos(wt) и свёртка исходного сигнала

2.2 Реализация модели преобразователя в среде MatLab. Формирование и анализ различных характеристик преобразователя Гильберта.

Краткое описание функции remez:

Функция remez синтезирует нерекурсивный (FIR) дискретный фильтр с линейной ФЧХ по методу Паркса-Макклеллана (Parks-McClellan). Его суть состоит в итерационном поиске фильтра, АЧХ которого максимально точно совпадает с заданной. Фильтры, синтезированные таким методом, характеризуются равномерными пульсациями АЧХ, поэтому их иногда называют фильтрами с равномерными пульсациями (equiripple filters). Из-за равномерности пульсаций АЧХ импульсная характеристика синтезированного фильтра может резко обрываться по краям (в отличие от фильтров, синтезированных с использованием окон, где края импульсной характеристики всегда спадают плавно).

Синтаксис: b = remez(n, f, a, ‘ftype’);

Возвращает вектор b длины n+1, содержащий коэффициенты нерекурсивного (FIR) фильтра, частотная характеристика которого задается векторами f и a. Векторы f и a задают амплитудно-частотную характеристику фильтра следующим образом:

• f — вектор пар частотных точек, лежащих в диапазоне от 0 до 1 (1 соответствует частоте Найквиста, то есть половине частоты дискретизации). Частоты должны образовывать неубывающую последовательность.

• a — вектор, содержащий значения желаемой АЧХ для частот из вектора f.

• Желаемая АЧХ на частотах между f(k) и f(k+1) при нечетном k определяется линейной функцией, соединяющей точки (f(k), a(k)) и (f(k+1), a(k+1)).

• Желаемая АЧХ на частотах между f(k) и f(k+1) при четном k считается неопределенной. Эти полосы частот считаются переходными или неважными.

Векторы f и a должны быть одной длины и содержать четное число элементов.

На рис. 2.2.1 показана желаемая АЧХ фильтра, сформированная с помощью функции Remez с векторами:

f = [0 0.3 0.4 0.6 0.7 0.9]

a = [0 1 0 0 0.5 0.5]

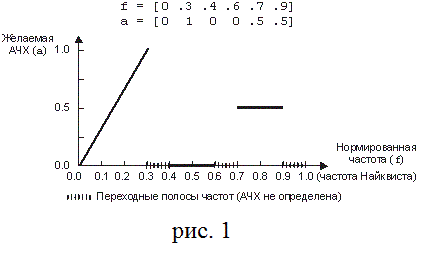
Рисунок 2.2.1 – пример реализации желаемоей АЧХ

фильтра с помощью функции remez

При формировании преобразователя Гильберта параметр ‘ftype’ == Hilbert. Преобразователь Гильберта имеет АЧХ равную единице во всём диапазоне рабочих частот.

Рассмотрим структурную схему, изображенную на рисунке 2.2.2 и реализуем её в MatLab.

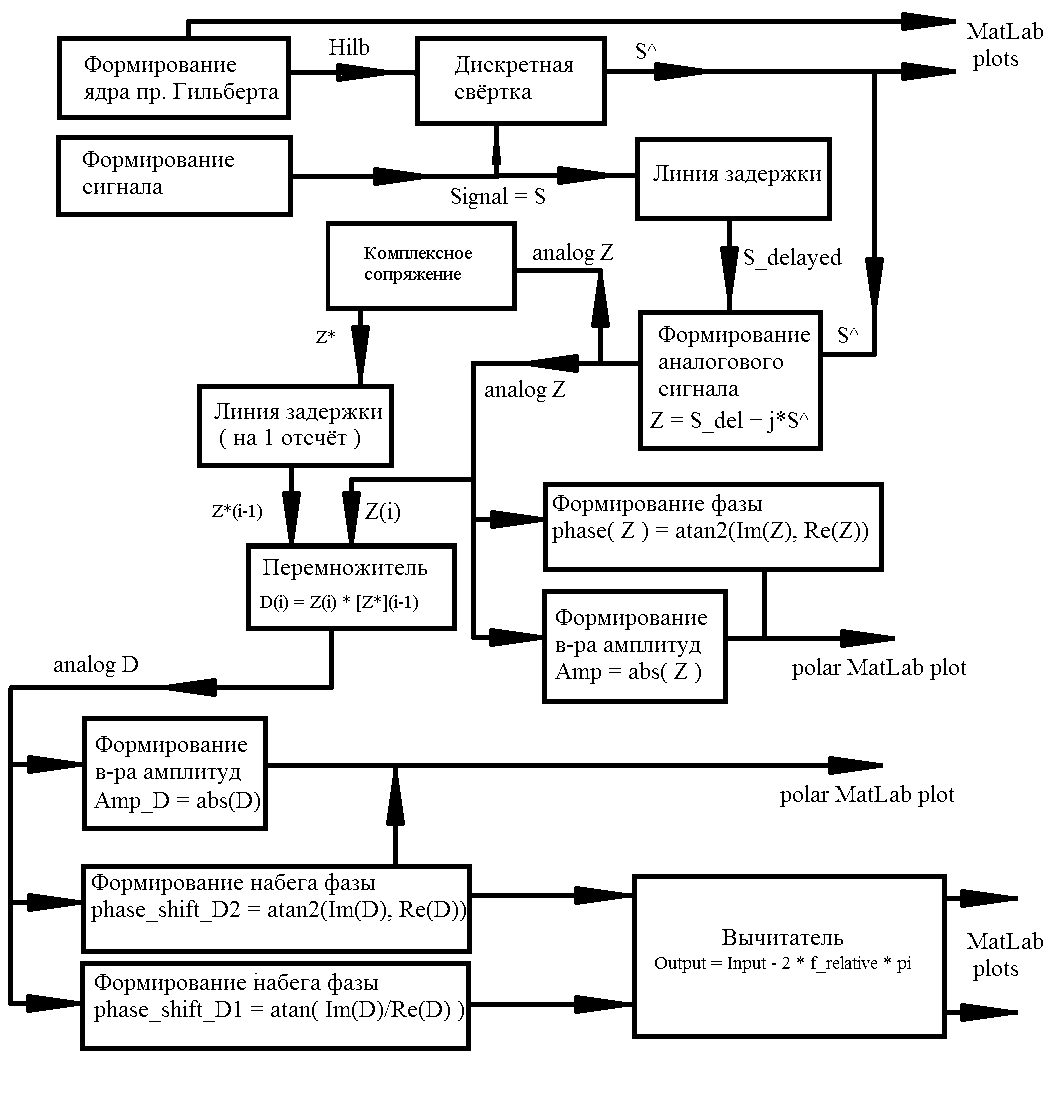
Рисунок 2.2.2 – Структурная схема, показывающая этапы исследования фазового шума в среде Matlab

Нам задан исходный сигнал S[i] , формируя ядро преобразования Гильберта Hilb[i], найдём сопряжённый по Гильберту сигнал:

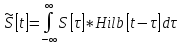
В нашем случае мы воспользуемся дискретной свёрткой. Стоит отметить, что далее под фазовым шумом будет пониматься разница между полученной фазой сигнала и фазой сигнала, полученной с помощью идеального преобразователя Гильберта.

Затем формируем аналитический сигнал 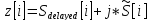, где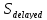- задержанный относительно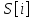сигнал. Находим для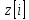комплексно сопряженный сигнал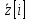. Учитывая, что сигнал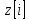получается с помощью неидеального преобразователя Гильберта, то в нём содержится фазовый шум ошибки предсказания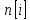. При экспоненциальном представлении аналитического сигнала:

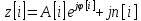
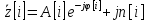
Далее согласно выражению формируем аналитический сигнал :

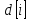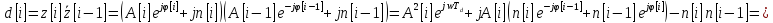
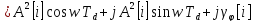
, где 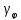- фазовый шум сигналаd,A– амлпитуда,T_d– период дискретизации,w- частота.

Тогда набег фазы равен :

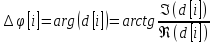
Учитывая, что

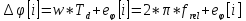, где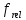– относительная частота,- искомая ошибка оценки фазы .

Получим:

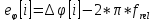
Далее реализуем эти операции в среде MatLab.

1. По желаемой АЧХ (рисунок 2.2.3) формируем преобразователь Гильберта:

% Формирование ядра пр. Гильберта

N = 100; % задаём порядок фильтра

% по заданным параметрам формируем ядро преобр. Гильберта

hilb = remez ( N , [0.1 0.9], [ 1 1 ] , ‘Hilbert’);

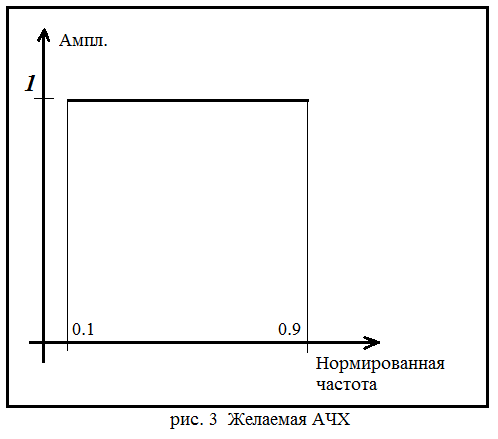
Рисунок 2.2.3 – Желаемая АЧХ

2. Формируем исходный сигнал:

% формируем исходный сигнал, задаём параметры:

M = 200 ; % кол-во отсчётов исходного сигнала

f_rel = 0.25; % относительная частота исходного сигнала, 4 отсчёта на период

S(1:M) = sin ( f_rel * 2 * pi * (0:M-1));

3. Дискретная свёртка:

% Производим дискретную свёртку:

S_linked( 1: (N + M) ) = 0;

for i = 1: (N + 1)

for j = 1:M

S_linked(i + j – 1) = S_linked(i + j – 1) + hilb(i) * S(j);

end

end

Также, для проверки правильности свёртки исходного синуса, произведём сравнение получившегося сигнала ( который, согласно теории должен стать отрицательным косинусом той же частоты) с отрицательным косинусом.

% Проверка результата свёртки Sin:

C_check( 1: (N + M) ) = -1 * cos ( f_rel * 2 * pi * ( (-N/2): (M + N/2 – 1) ) );

figure(1);

plot(0: (N + M – 1), S_linked, N/2: (N+M – 1), C_check( (N/2 + 1): (N+M) ) );

Получим следующий график ( рисунок 2.2.4 ).

Проведя краткий анализ рисунка 2.2.4 мы увидим, что полученная модель преобразователя согласовывается с теорией, и исходная синусная гармоника перешла косинусную.

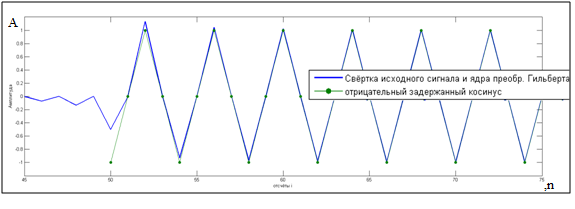
Рисунок 2.2.4 – График сравнения результата преобразования и результата идеального преобразования Гильберта

4. Линия задержки исходного сигнала:

% Задержим исходный сигнал:

S_delayed( 1: (N + M) ) = sin ( f_rel * 2 * pi * ((-N/2): (M + N/2 – 1)) );

% Формирование аналогового сигнала:

Z = S_delayed + sqrt(-1) * S_linked;

% Формирование вектора фазы:

phase_Z = atan2( imag(Z), real(Z) );

% Формирование вектора амплитуды:

amp_Z = abs( Z );

7. Строим график в полярный координатах:

polar( phase_Z(N/2:M+N/2), amp_Z(N/2:M+N/2));

Проведём краткий анализ риснука 2.2.5. Если бы этот сигнал был аналоговым (непрерывным по уровню и по времени), то его графиком в полярный координатах была бы окружность. Но учитывая, что мы берём отсчёты сигнала с частотой 4 отсчёта на период, то мы получили четырёхугольник. В итоге,результат оправдывает ожидания.

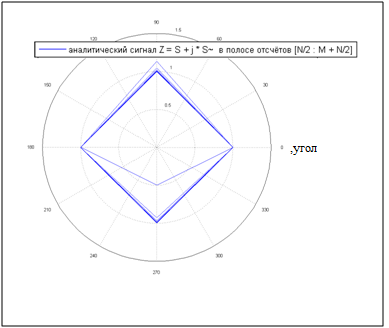
Рисунок 2.2.5 – График полученного в пункте 6 аналитического сигнала

8. Формирование аналитического сигнала D:

%Создаём комлпексно сопряженный сигнал Z_compl:

Z_compl = S_delayed – sqrt(-1) * S_linked;

% Формируем аналитический сигнал D:

for i = 1:N+M-1

D(i+1) = Z(i+1) * Z_compl(i);

end

9. Нахождение конечных параметров:

%Находим набег фазы:

phase_shift = atan2(imag(D), real(D));

%Находим фазовый шум:

n(2:N+M) = phase_shift(2:N+M) – 2*pi*f_rel;

На рисунках 2.2.6 и 2.2.7 изображены полученные графики фазового шума

(График, изображенный на рисунке 2.2.6 симметричен относительно центрального отсчёта ( [N+M] /2 )

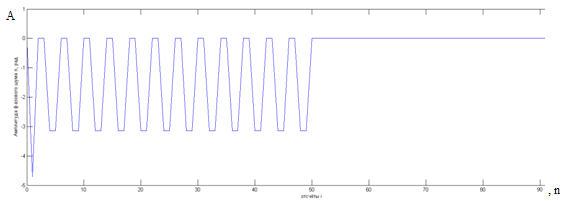
Рисунок 2.2.6 – график зависимости фазового шума от номера отсчёта

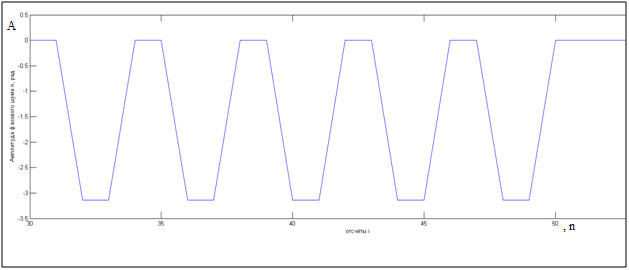
Рисунок 2.2.7 – Переходный участок графика зависимости

фазового шума от номера отсчёта