
2.7.1 Расчет технологических параметров для кожуха хк-250-00.000.02
Исходные данные:
наименование изделия – «кожух ХК-250-00.000.02»;
полимер – УПС 825;
показатель текучести расплава ПТР=7,5 г/10мин. по ГОСТ 11645-73
габариты изделия: средняя толщина стенки изделия δ = 2,5 мм
длина L=525 мм
ширина s =392 мм
масса изделия Gg=800 гр.
масса литникового остатка Gло=9,8 гр.
гнездность формы N
 =1
=1
2.7.1.1 Определение температуры расплава
Расчет температуры литья производится с использованием реологических характеристик полимера.
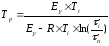 ,
,
где
Еу-
энегия активации при скорости сдвига
γi,
Еу
=42000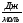 ;
;
Ti- температура определения показателя текучести расплава,
Ti=200º+273=473К;
τi – напряжение сдвига при определении показателя текучести расплава
τi =21000 Па;
τп - напряжение сдвига в области переработки при скорости сдвига равное γi
τп= 18000 Па
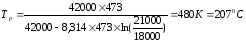
2.7.1.2 Расчет площади основного изделия – кожуха ХК-250-00.000.02 в плоскости разъема формы
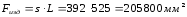 ,
(3.1)
,
(3.1)
2.7.1.3 Расчет основных параметров литниковой системы
Центральный конический (стержневой) канал
Радиус
минимальный
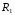 =
4 мм;
=
4 мм;
Радиус
максимальный
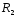 =
7 мм;
=
7 мм;
Длина
канала
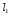 =
78 мм.
=
78 мм.
Определяем скорость сдвига на первом участке [2, с.202]:
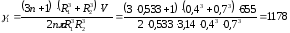
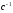 , (3.4)
, (3.4)
Показатель степени может быть найден из расчетной номограммы по средней линии для области, соответствующей методу переработки. Для этого, взяв 2 точки на средней линии этой области, по скорости сдвига и напряжению сдвига, соответствующих этим точкам, производят расчет по уравнению [2, с.201]:
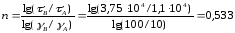 , (3.5)
, (3.5)
где
координаты точки А –
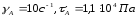 ,
,
координаты
точки В –
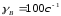 ,
,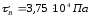
Находим напряжение сдвига [5, с.170]:
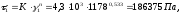 (3.7)
(3.7)
где К=4,3 ∙103 – усредненное значение коэффициента реологического уравнения
Потери давления будут равны [1, с.173]:
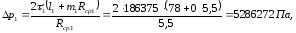 (3.8)
(3.8)
где m1 = 0 – входной коэффициент (на данном участке имеется один канал, и расплав из канала мундштука в него входит без резкого изменения скорости);
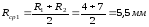 –средний
радиус канала
–средний
радиус канала
Суммарный перепад давления в литниковой системе:
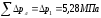 (3.16)
(3.16)
2.7.1.4 Определение температуры расплава после впрыска и сжатия расплава полимера
Температуру расплава после впрыска и сжатия полимера можно найти по уравнению [1, с.282]:
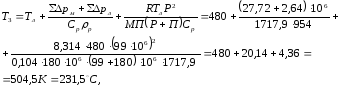
(3.17)
где
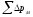 =
27,72 МПа– суммарные потери давления в
мундштуке [7,с.169];
=
27,72 МПа– суммарные потери давления в
мундштуке [7,с.169];
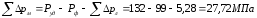 (3.18)
(3.18)
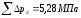 –суммарные
потери давления в каналах литниковой
системы, определенные исходя из количества
расчетных участков и их длины; М=0,104
кг/моль; П=180 МПа – коэффициенты уравнения
термодинамики [1, с.91];
–суммарные
потери давления в каналах литниковой
системы, определенные исходя из количества
расчетных участков и их длины; М=0,104
кг/моль; П=180 МПа – коэффициенты уравнения
термодинамики [1, с.91];
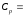 0,41
ккал/г·град = 1717,9 Дж/кг·К – удельная
теплоемкость, при температуре Тл=207
°С [8, с.43];
0,41
ккал/г·град = 1717,9 Дж/кг·К – удельная
теплоемкость, при температуре Тл=207
°С [8, с.43];
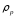 =
954 кг/м³– плотность расплава полимера
при температуре Тл=207
°С [8,с.45];
=
954 кг/м³– плотность расплава полимера
при температуре Тл=207
°С [8,с.45];
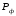 =
99 МПа – давление в полости формы
=
99 МПа – давление в полости формы
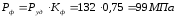 (3.19)
(3.19)
где
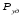 =
132 МПа – удельное давление литья;
=
132 МПа – удельное давление литья;
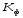 =
0,75 – коэффициент, который при литье
тонкостенных изделий [1,с.261].
=
0,75 – коэффициент, который при литье
тонкостенных изделий [1,с.261].

2.7.1.5 Время выдержки под давлением
Время выдержки под давлением находят с учетом условий:
– находят время, когда температура расплав в середине центрального литника или на каком-либо другом участке понижается до температуры текучести Тт;
–находят время, при котором температура изделия около впускного литника понижается до температуры текучести [1, с.285].
За время выдержки под давлением принимается минимальное значение из всех найденных величин [1, с.286].
Центральный конический (стержневой) канал
Радиус
минимальный
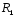 =
4 мм;
=
4 мм;
Радиус
максимальный
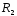 =
7 мм;
=
7 мм;
Длина
канала
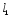 =
78 мм.
=
78 мм.
Средний
радиус канала
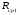 =
5,5 мм.
=
5,5 мм.
Время выдержки под давлением [1, с.285]:
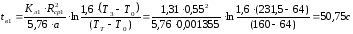 (3.20)
(3.20)
где Т0 = 64˚С – температура охлаждающей поверхности формы;
а
=
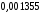 см²/с
– коэффициент температуропроводности
расплава;
см²/с
– коэффициент температуропроводности
расплава;
Т3 = 231,5 ˚С – температура расплава после впрыска и сжатия;
Rср1 = 0,55 см – средний радиус конического литника.
Температура охлаждающей поверхности формы определяется по формуле [1, с.285]:
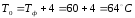 ,
(3.21)
,
(3.21)
где
Тф
–
температура формы,
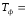 60 ˚С
60 ˚С
Коэффициент температуропроводности:
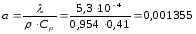 см²/с,
(3.22)
см²/с,
(3.22)
где
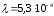 кал/см·с·град
– теплопроводность расплава полимера
при температуре Тл
=207
°С [6, с.20];
кал/см·с·град
– теплопроводность расплава полимера
при температуре Тл
=207
°С [6, с.20];
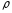 =
0,954 г/см³ – плотность расплава полимера
при температуре Тл
=
207 °С [6, с.28];
=
0,954 г/см³ – плотность расплава полимера
при температуре Тл
=
207 °С [6, с.28];
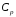 =
0,41 кал/г·град – теплоемкость расплава
полимера при температуре Тл
=
207°С [6, с.19].
=
0,41 кал/г·град – теплоемкость расплава
полимера при температуре Тл
=
207°С [6, с.19].
Поправочный
коэффициент Кл1,
учитывающий течение расплава через
литник в момент подпитки формы расплавом
[8, с.58]:
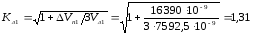 ,
(3.23)
,
(3.23)
где
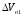 – объем расплава, нагнетаемый в форму
во время выдержки под давлением;
– объем расплава, нагнетаемый в форму
во время выдержки под давлением;
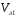 –объем
литника на расчетном участке.
–объем
литника на расчетном участке.
Объем подпитки равен [7, с.60]:
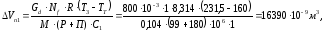
(3.24)
где
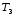 =
231,5 °С – температура расплава после
впрыска;
=
231,5 °С – температура расплава после
впрыска;
Тт=160 °С – температура текучести;
М=0,104 кг/моль,
П =180 МПа – коэффициенты уравнения состояния;
Gизд
=800 г – масса изделия;
Nf=1 – гнездность формы;
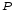 =
99 МПа– давление в полости формы;
=
99 МПа– давление в полости формы;
С1=1 – количество параллельных каналов на расчетном участке.
Объем центрального конического литника:
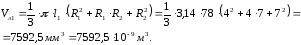
(3.25)
Время выдержки также может быть обусловлено временем охлаждения расплава в формующей полости. В этом случае время выдержки под давлением для изделия в виде пластины или втулки определяют по формуле [1, с.28]:
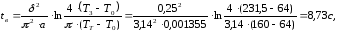
(3.30)
где
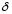 =
2,5 мм = 0,25 см – толщина изделия;
=
2,5 мм = 0,25 см – толщина изделия;
а
=
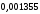 см²/с
– коэффициент температуропроводности
при средней температуре
см²/с
– коэффициент температуропроводности
при средней температуре
За
время выдержки под давлением принимаем
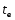 =
8,73 с
=
8,73 с
2.7.1.6 Определение времени выдержки при охлаждении
При литье изделий, имеющих внутреннюю полость, время охлаждения рассчитывается так же, как для пластины, поскольку время охлаждения зависит от размеров изделия, через которое происходит теплопередача [6, с.62]:
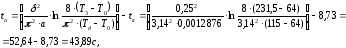
(3.31)
где
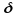 =
0,25 см– толщина изделия,
=
0,25 см– толщина изделия,
Тд
– средняя температура изделия по толщине
стенки после извлечения его из формы;
а – коэффициент температуропроводности, находится при средней температуре ;
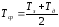 .
(3.32)
.
(3.32)
Для кристаллических полимеров средняя температура изделия по толщине стенки после извлечения его из формы [2, с.287]:
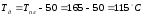 ,
(3.33)
,
(3.33)
Средняя температура:
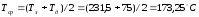
Коэффициент
температуропроводности при
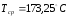 :
:
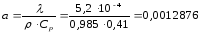 см²/с,
см²/с,
где
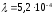 кал/см·с·град – теплопроводность
полимера при Тср
=173,25
°С [8, с.45];
кал/см·с·град – теплопроводность
полимера при Тср
=173,25
°С [8, с.45];
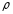 =0,985
г/см³ – плотность расплава полимера
при температуре Тср
=
173,25 °С [8, с.45];
=0,985
г/см³ – плотность расплава полимера
при температуре Тср
=
173,25 °С [8, с.45];
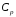 =
0,41 кал/г·град – теплоемкость расплава
при температуре Тср
=
173,25 °С [8, с.43].
=
0,41 кал/г·град – теплоемкость расплава
при температуре Тср
=
173,25 °С [8, с.43].
2.7.2.1 Расчет технологических параметров для корпуса воздуховода подачи NF 1.1.1.1.0.0.1
Исходные данные:
наименование изделия – «корпус воздуховода подачи NF 1.1.1.1.0.0.1»;

полимер ПЭ2НТ22-12;
показатель текучести расплава ПТР =7 г/10мин. по ГОСТ 11645-73
габариты изделия: средняя толщина стенки изделия δ =2 мм.;
длина изделия L=L1+L2+L3=265+178+61=504 мм.;
ширина изделия S=85 мм;
масса изделия Gg=245 гр;
масса литникового остатка Gло=22,8 гр;
гнездность формы N
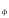 =2
=2
2.7.2.2 Расчет площади основного изделия « корпус воздуховода подачи
NF 1.1.1.1.0.0.1» в плоскости разъема формы
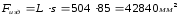
Расчет площади литниковой системы в плоскости разъема формы:
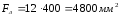
2.7.2.3 Расчет основных параметров литниковой системы
Расчетный участок 1
Центральный конический (стержневой) канал
Радиус
минимальный
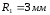 ;
;
Радиус
максимальный
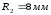 ;
;
Длина
канала
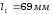 .
.
Определяем скорость сдвига на первом участке [1, с.202]:
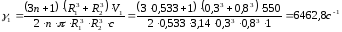 ,
,
Показатель степени n может быть найден из расчетной номограммы по средней линии для области, соответствующей методу переработки. Для этого, взяв 2 точки на средней линии этой области, по скорости сдвига и напряжению сдвига, соответствующих этим точкам, производят расчет по уравнению [1,с.41]:
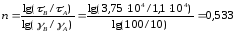 , (3.5)
, (3.5)
где
координаты точки А –
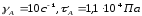 ,
,
координаты
точки В –
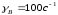 ,
,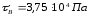
В отличие от сбалансированной системы объемная скорость течения на отдельных участках непостоянная, поэтому объемный расход в каждой расчетной ветви равен [7, с.179]:
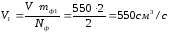 ,
,
где
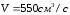 –
объемная скорость машины;
–
объемная скорость машины;
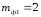 –количество
формующих полостей, питаемых данным
участком литниковой системы;
–количество
формующих полостей, питаемых данным
участком литниковой системы;
Nф =2– гнездность формы.
Находим напряжение сдвига [7, с.168]:
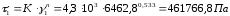 ,
,
где К=4,3∙103 – усредненное значение коэффициента реологического уравнения для 5 области переработки [2, с.196].
Потери давления будут равны [7, с.173]:
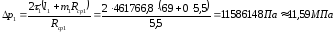 ,
,
где m1 =0 – входной коэффициент (на данном участке имеется один канал, и расплав из канала мундштука в него входит без резкого изменения скорости);
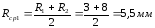 –средний
радиус канала.
–средний
радиус канала.
Расчетный участок 2
Разводящий прямоугольный канал
Глубина прямоугольной части канала h2= 7 мм;
Ширина канала b2=13 мм;
Длина
канала
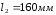 .
.
Определяем скорость сдвига на втором участке [7, с.173]:
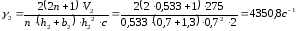 ,
,
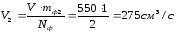 –объемный
расход в расчетной ветви;
–объемный
расход в расчетной ветви;
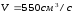 –объемная
скорость машины;
–объемная
скорость машины;
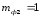 –количество
формующих полостей, питаемых данным
участком литниковой системы;
–количество
формующих полостей, питаемых данным
участком литниковой системы;
Nф =2– гнездность формы [7, с.179].
Находим напряжение сдвига [7, с.168]:
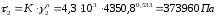 ,
,
где
К=4.3∙103
–
усредненное значение коэффициента
реологического уравнения для 5 области
переработки [2, с.196].
Потери давления будут равны [11, с.173]:
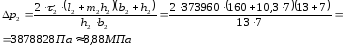
где
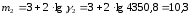 –
входной коэффициент [2, с.202] (на данном
участке имеется поворот от предыдущего
канала)
–
входной коэффициент [2, с.202] (на данном
участке имеется поворот от предыдущего
канала)
Расчетный участок 3
Прямоугольный канал канал
Глубина прямоугольной части канала h2= 7 мм;
Ширина канала b2=6 мм;
Длина
канала
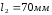 .
.
Определяем скорость сдвига на втором участке [7, с.173]:
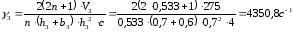 ,
,
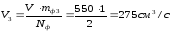 –объемный
расход в расчетной ветви;
–объемный
расход в расчетной ветви;
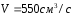 –объемная
скорость машины;
–объемная
скорость машины;
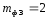 –количество
формующих полостей, питаемых данным
участком литниковой системы;
–количество
формующих полостей, питаемых данным
участком литниковой системы;
Nф = 2 – гнездность формы
Находим напряжение сдвига [2, с.196]:
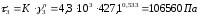 ,
,
где К=4.3∙103 – усредненное значение коэффициента реологического уравнения для 5 области переработки [2, с.196].
Потери давления будут равны [2, с.202]:
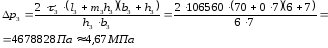 ,
,
Суммарный перепад давления в литниковой системе:
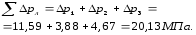

2.7.2.5 Определение температуры расплава
Расчет температуры литья производится с использованием реологических характеристик полимера.
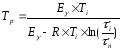 ,
,
где
Еу
-
энегия активации при скорости сдвига
γi,
Еу
=17000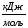 ;
;
Ti- температура определения показателя текучести расплава,
Ti=190+273=463К; τi – напряжение сдвига при определении показателя текучести расплава τi =9000 Па; τп - напряжение сдвига в области переработки при скорости сдвига равное γi τп= 18000 Па
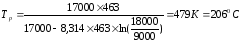

2.7.2.4 Определение температуры расплава после впрыска и сжатия расплава полимера
Температуру расплава после впрыска и сжатия полимера можно найти по уравнению [2, с.282]:
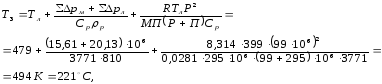
где
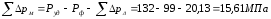 –
суммарные потери давления в мундштуке
[2, с.181];
–
суммарные потери давления в мундштуке
[2, с.181];
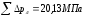 –суммарные
потери давления в каналах литниковой
системы, определенные исходя из количества
расчетных участков и их длины;
–суммарные
потери давления в каналах литниковой
системы, определенные исходя из количества
расчетных участков и их длины;
М=0,0281 кг/моль, П =295 МПа – коэффициенты уравнения термодинамики [1, с.91];
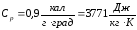 –удельная
теплоемкость, при температуре Тл=206
°С [8, с.19];
–удельная
теплоемкость, при температуре Тл=206
°С [8, с.19];
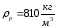 –плотность
расплава полимера при температуре
Тл=206
°С [8,с.25];
–плотность
расплава полимера при температуре
Тл=206
°С [8,с.25];
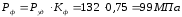 –давление
в полости формы
–давление
в полости формы
где
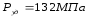 –
удельное давление литья;
–
удельное давление литья;
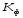 –коэффициент,
который при литье тонкостенных изделий
примерно равен 0,75 [1, с.261].
–коэффициент,
который при литье тонкостенных изделий
примерно равен 0,75 [1, с.261].
2.7.2.5 Определение времени выдержки под давлением
Время выдержки под давлением находят с учетом условий:
находят время, когда температура расплав в середине центрального литника или на каком-либо другом участке понижается до температуры текучести Тт;
находят время, при котором температура изделия около впускного литника понижается до температуры текучести. [1, с.285].
За время выдержки под давлением принимается минимальное значение из всех найденных величин. [1, с.286]. Учитывая то, что применяются каналы довольно большого сечения относительно толщины стенки изделия, понятно, что их время выдержки под давлением намного больше, поэтому рассчитаем только самый узкий участок - туннельный конический впускной канал.
Расчетный участок 3
Разводящий прямоугольный канал
Глубина прямоугольной части канала h2= 7 мм;
Ширина канала b2=6 мм;
Длина
канала
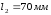 .
.
Время выдержки под давлением [1, с .285]:
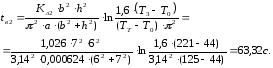
Поправочный
коэффициент Кл2,
учитывающий течение расплава через
литник в момент подпитки формы расплавом
[4, с.19]:
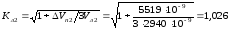
Объем подпитки равен [4, с.19]:
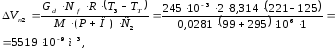
где С2=1 – количество параллельных каналов на расчетном участке.
Объем литника:
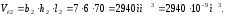
Для кристаллических полимеров средняя температура изделия по толщине стенки после извлечения его из формы [2, с.287]:
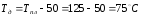 ,
(3.33)
,
(3.33)
Средняя температура:
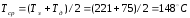
Коэффициент
температуропроводности при
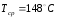 :
:
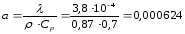 см²/с,
см²/с,
где
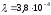 кал/см·с·град – теплопроводность
полимера при
кал/см·с·град – теплопроводность
полимера при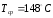 [8, с.16];
[8, с.16];
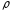 =0,87
г/см³ – плотность расплава полимера
при температуре
=0,87
г/см³ – плотность расплава полимера
при температуре
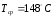 [8, с.16];
[8, с.16];
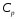 =
0,7 кал/г·град – теплоемкость расплава
при температуре
=
0,7 кал/г·град – теплоемкость расплава
при температуре
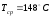 [8, с.15].
[8, с.15].
Время выдержки также может быть обусловлено временем охлаждения расплава в формующей полости. В этом случае время выдержки под давлением для изделия в виде пластины или втулки определяют по формуле [1, с.285]:
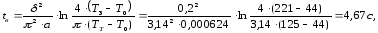
где
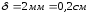 – толщина стенки изделия возле впускного
литника (см. чертеж изделия).
– толщина стенки изделия возле впускного
литника (см. чертеж изделия).
За
время выдержки под давлением принимаем
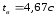 .
.
2.7.2.6 Определение времени выдержки при охлаждении
При литье изделий, имеющих внутреннюю полость, время охлаждения рассчитывается так же, как для пластины, поскольку время охлаждения зависит от размеров изделия, через которое происходит теплопередача [1, с.286]:
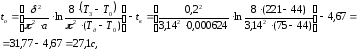
где
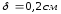 –
максимальная толщина изделия;
–
максимальная толщина изделия;
