Степенные ряды.

Ряд вида:

,

где  постоянные, называется степенным.

Теорема Абеля. Если степенной ряд , при сходится(расходится) при некотором значении , то он сходится(расходится) при всяком значении .

Число называется радиусом сходимости степенного ряда, а интервал интервалом сходимости, если:

1. ряд абсолютно сходится, при ;

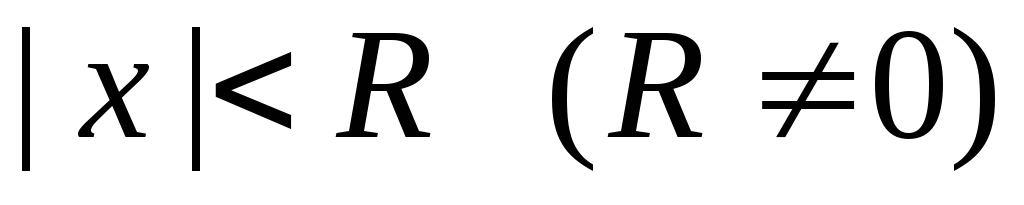2. ряд расходится, при .

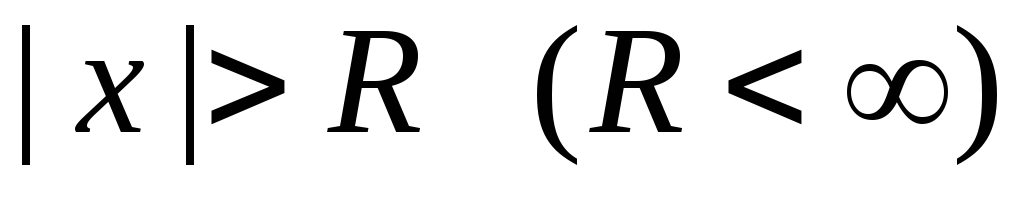Радиус сходимости степенного ряда определяется по формулам:

;

.

Свойства степенных рядов:

1. Степенной ряд сходится равномерно на любом отрезке , где 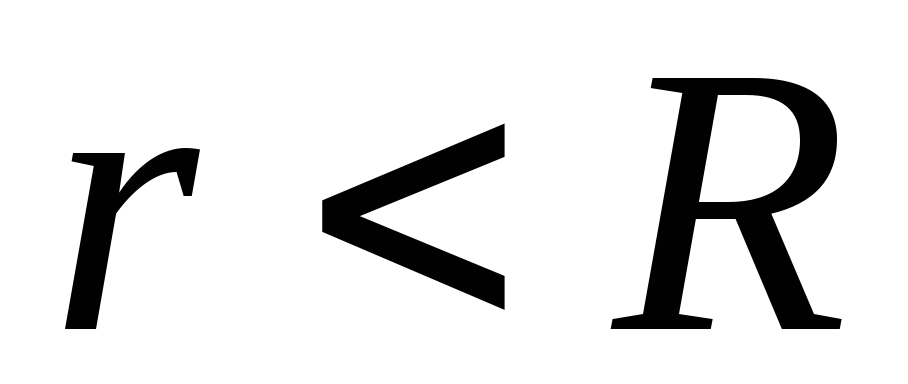,  радиус сходимости.

2. Сумма степенного ряда есть непрерывная на отрезке 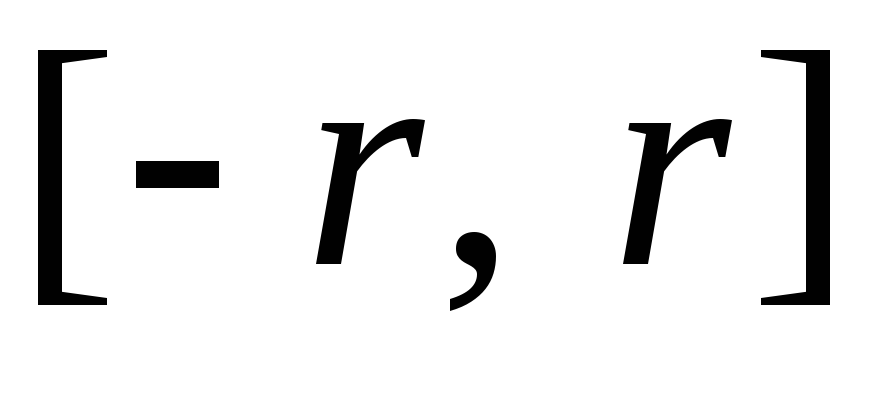функция.

3. Степенной ряд можно почленно интегрировать на любом отрезке и почленно дифференцировать в интервале .

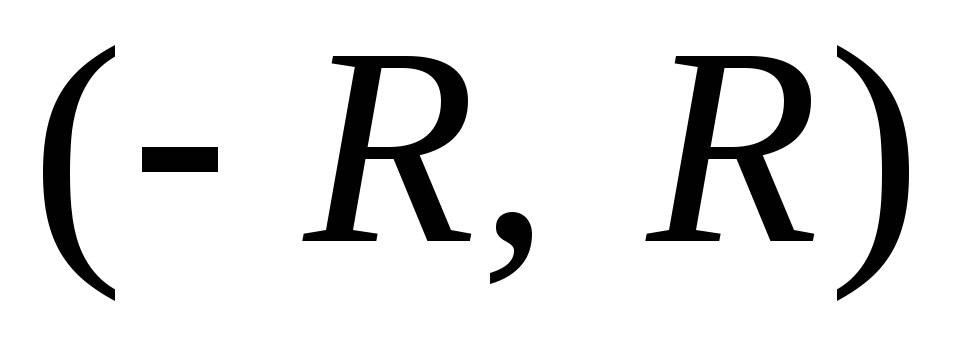Пример. Определить радиус и интервал сходимости и исследовать поведение в граничных точках интервала сходимости: .

Решение:

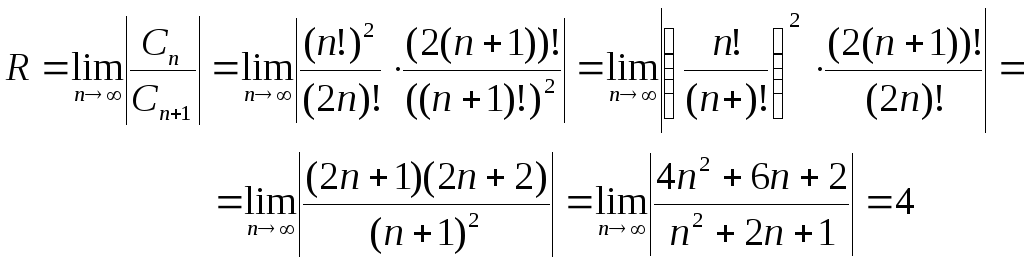
Ряд сходится при , а расходится при

При , получаем ряд , применим к нему необходимый признак сходимости:

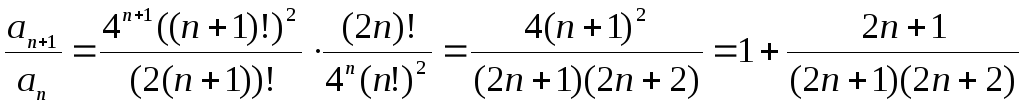1. , т.е. . Следовательно, последовательность 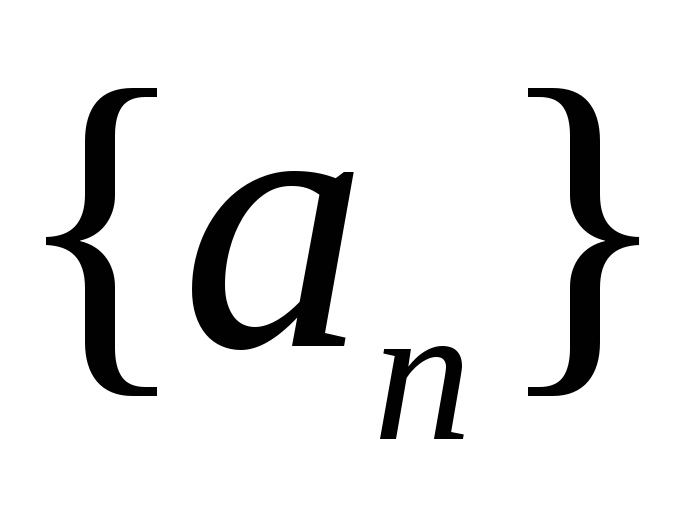монотонно возрастает.

2. , т.е. общий член ряда не стремится к нулю, т.е. ряд расходится.

Аналогично, при .

Ответ: , интервал сходимости .

Ряд Тейлора и Маклорена.

Если функция имеет производные любого порядка в окрестности точки , то для функции получим бесконечный ряд, который называется рядом Тейлора:

,

где называется остаточным членом ряда.

Ряд Тейлора сходится к функции тогда и только тогда, когда .

Если все производные ограничены , где то .

Положим , тогда получим частный случай ряда Тейлора, который называется рядом Маклорена:

.

Разложение в ряд Маклорена основных функций:

1. ;

2. ;

3. ;

4. ;

5. .

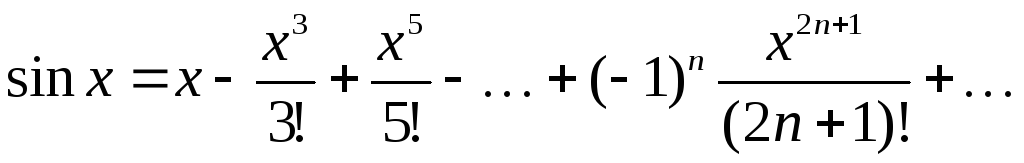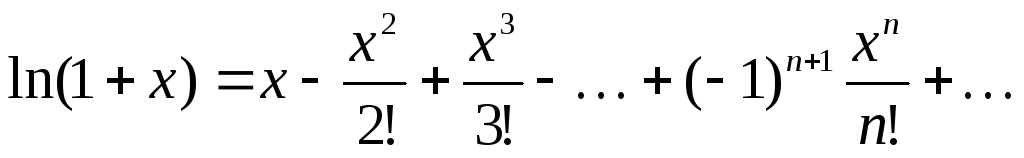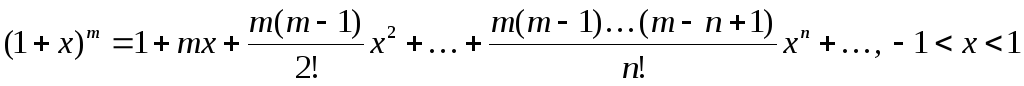Пример. Пользуясь разложениями написать разложение в степенной ряд относительно следующей функции: .

Решение: Преобразуем .

, ,

.

Ответ: .

Пример. Разложить в ряд Тейлора функцию по степеням .

Решение: Преобразуем данную функцию:

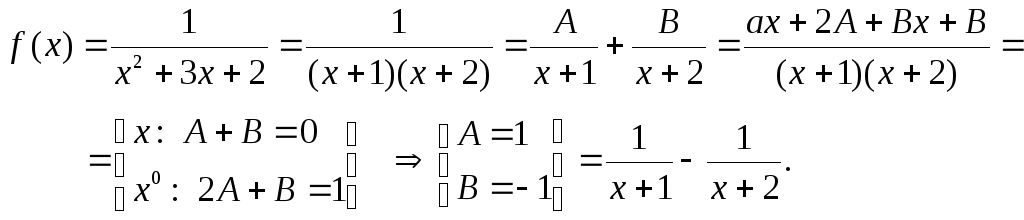
Находим значение функции и ее производных в точке :

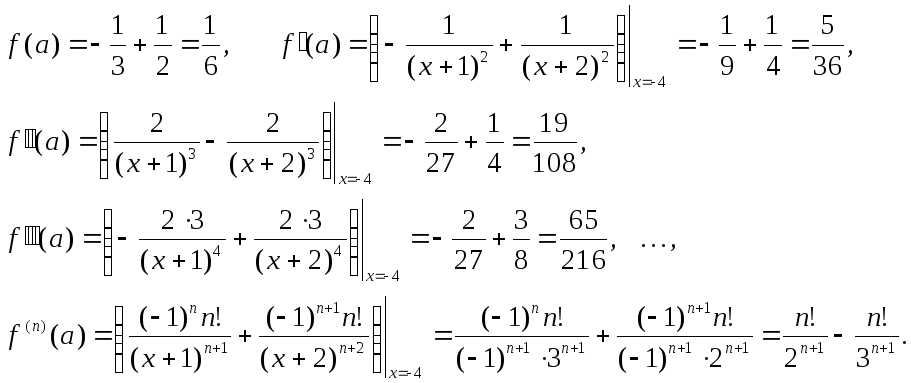
Подставляем полученное в формулу Тейлора:

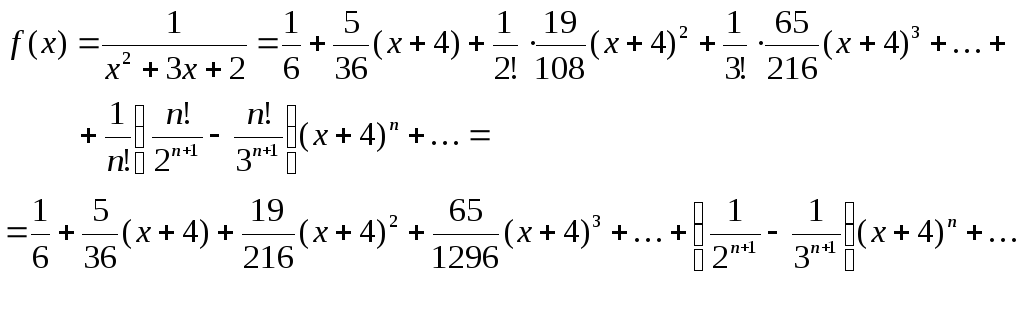
Ответ: .

Задания для самостоятельной работы.

1. Найти суммы следующих рядов:

А) ; Б) ;

В) ;

Г) ;

Д) .

2. Доказать расходимость рядов:

А) ; Б) ;

В) ; Г) .

3. Используя признаки сравнения исследовать сходимость рядов:

А) ; Б) ;

В) ; Г) .

4. Используя признаки Даламбера или Коши, исследовать сходимость следующих рядов:

   А) ;	Б) ;	В) ;
   Г) ;	Д) .

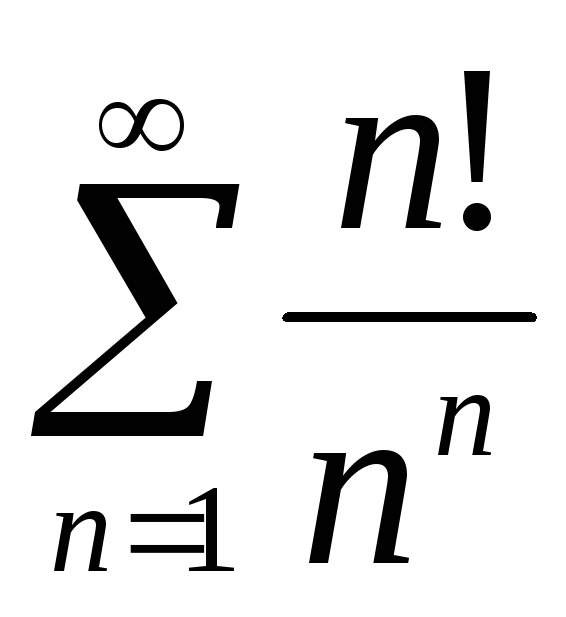5. Пользуясь интегральным признаком, исследовать сходимость следующих рядов:

   А) 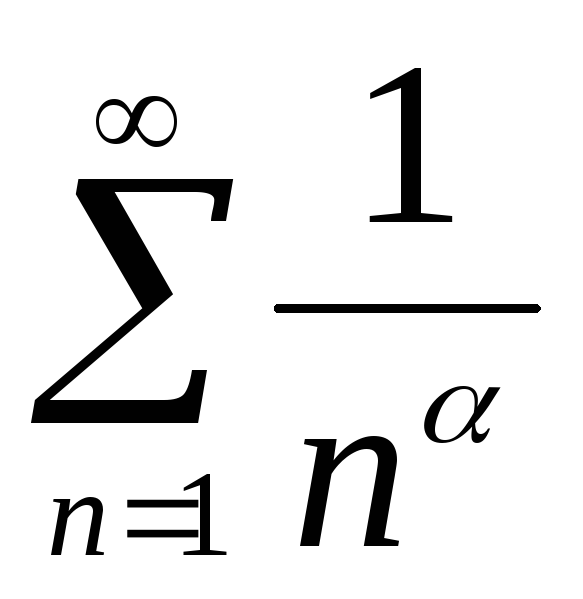;	Б) 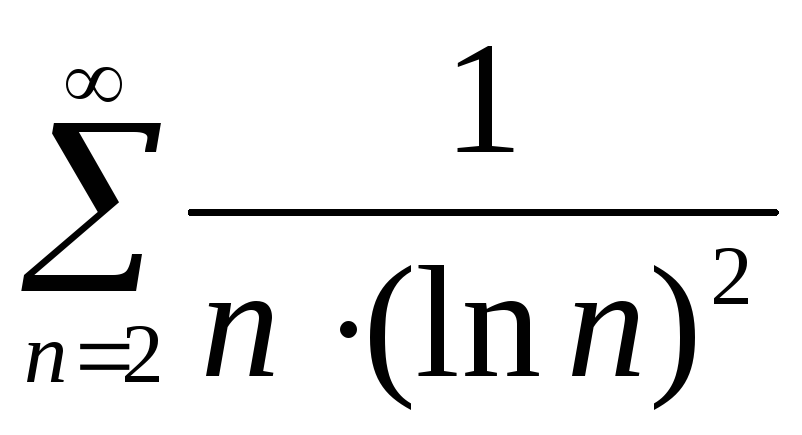;	В) ;
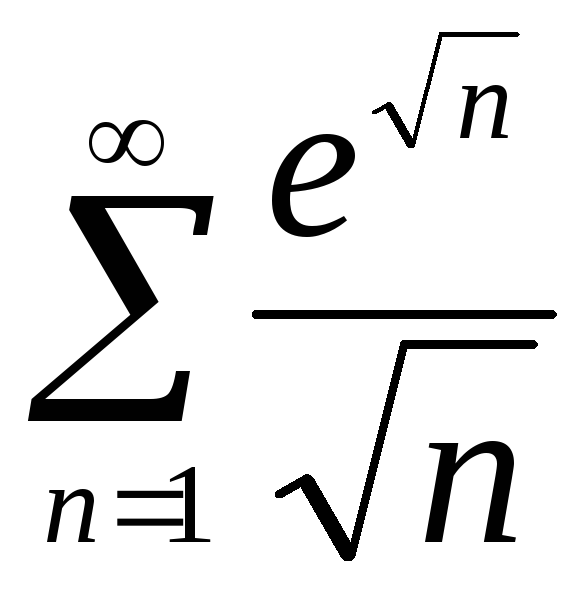   Г) 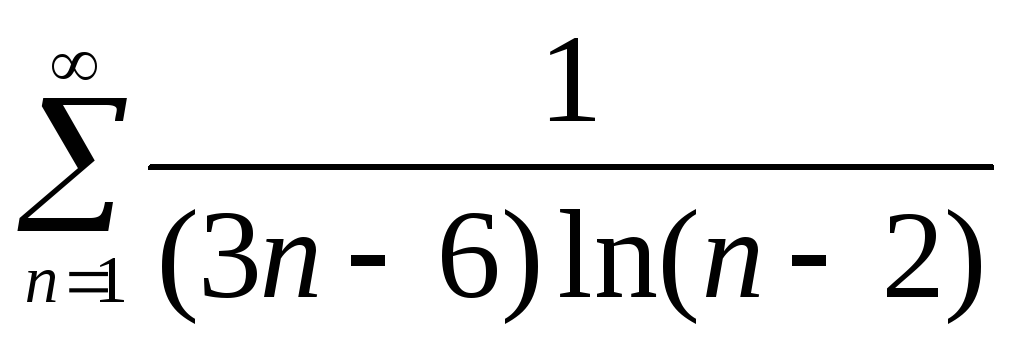;	Д) .

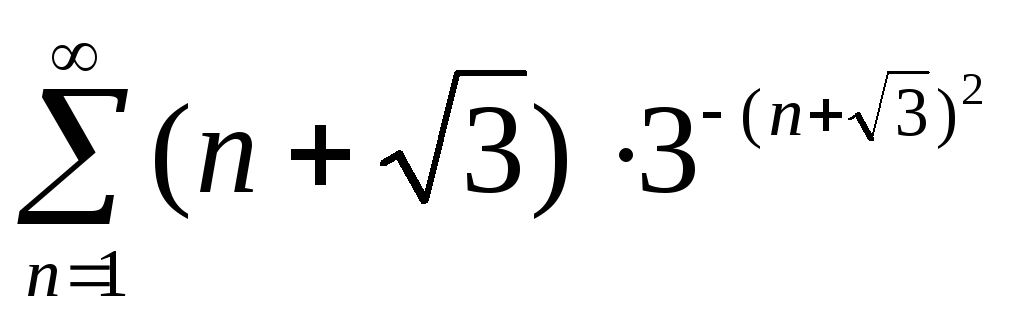6. Исследовать на абсолютную и условную сходимость:

   А) ;	Б) ;	В) ;
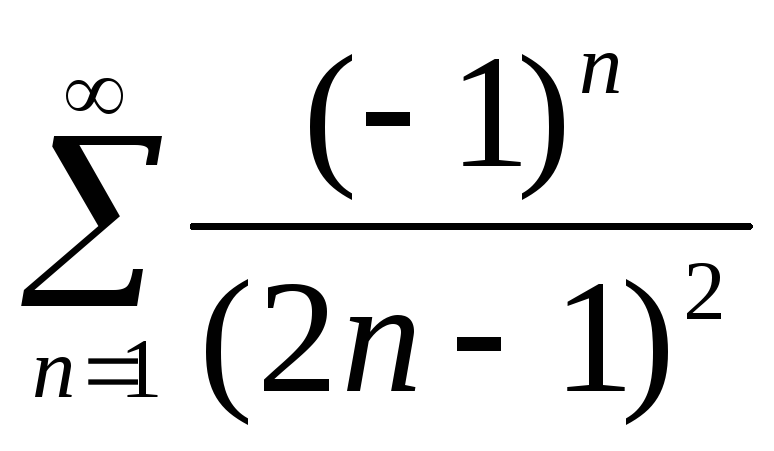   Г) ;	Д) .

7. Определить интервал сходимости степенного ряда и исследовать его сходимость на границах интервала:

   А) 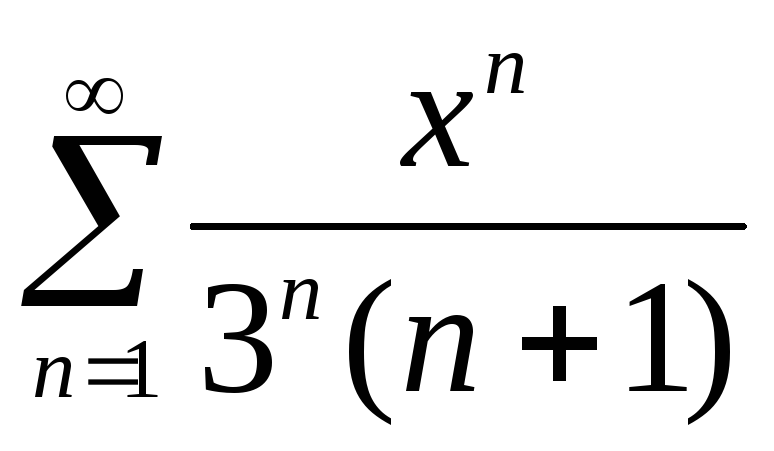;	Б) 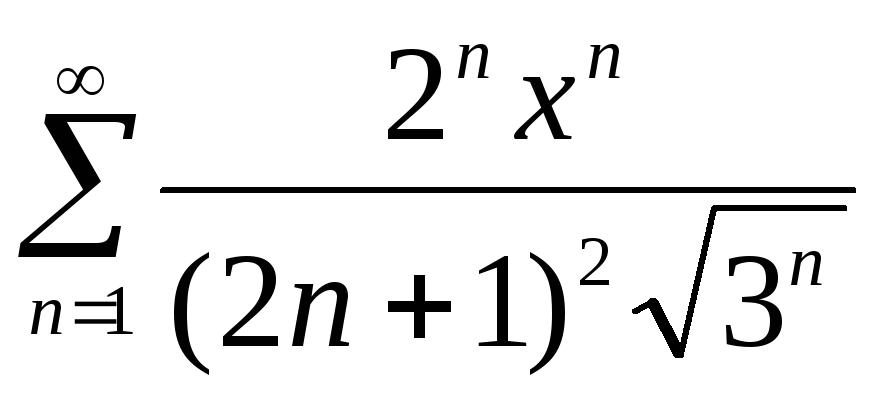;	В) ;
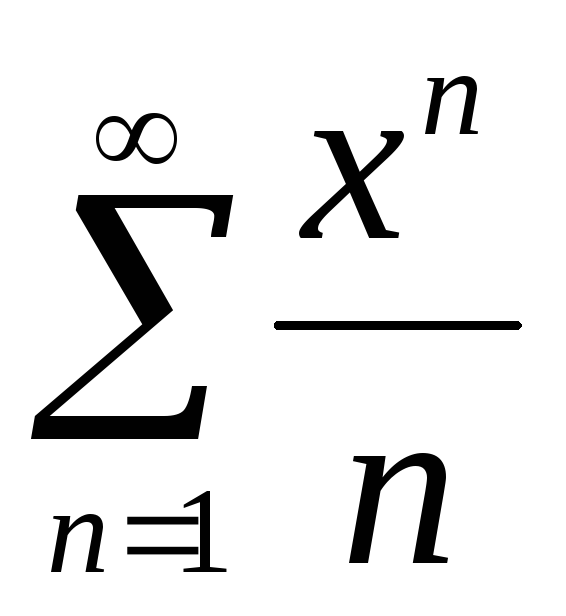   Г) ;	Д) .

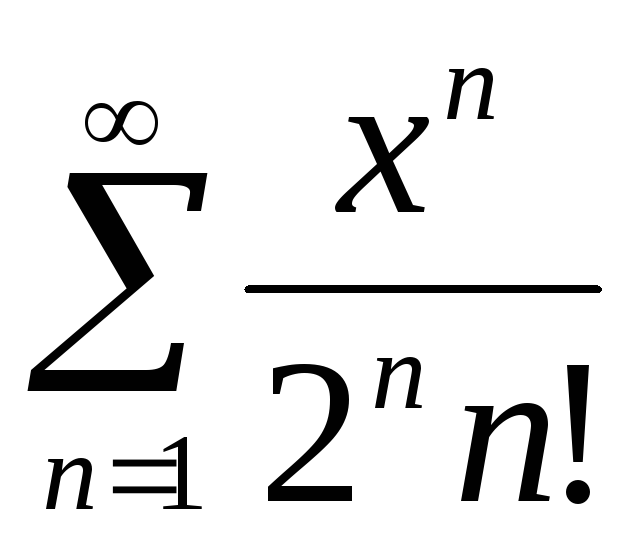8. Пользуясь разложениями элементарных функций в ряд, написать разложение в степенной ряд следующих функций:

   А) 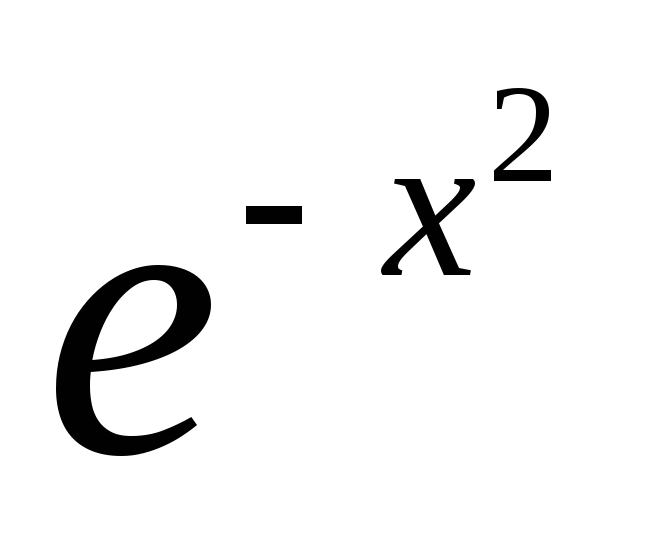;	Б) ;	В) ;
   Г) 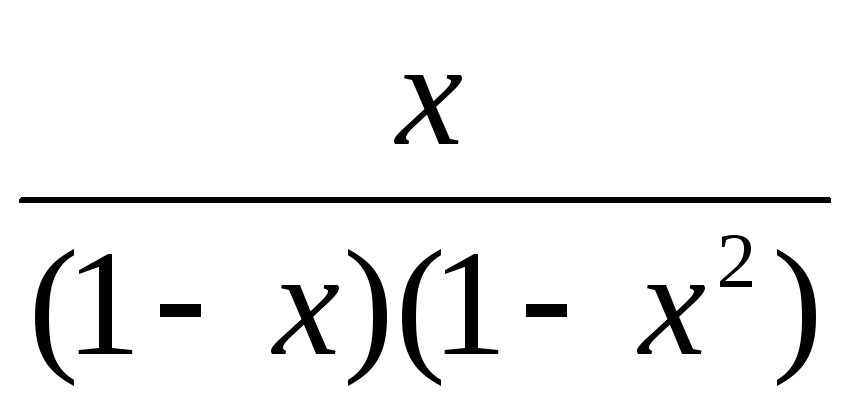;	Д) .

9. Разложить в ряд Тейлора:

А) по степеням ; Б) по степеням ;

В) по степеням ; Г) по степеням .