Ряды

Выражение вида , представляющее собой последовательность действительных или комплексных чисел , соединенных знаком плюс, называется числовым рядом. Числа называются членами ряда, а  общим членом ряда.

Сумму первых членов ряда называют -й частичной суммой числового ряда.

Числовой ряд называется сходящимся, если существует конечный предел последовательности частичных сумм ряда , т.е., где сумма числового ряда, т.е. , в противном случае, ряд называется расходящимся.

Необходимый признак сходимости ряда. Если ряд сходится, то .

Числовой ряд , полученный из ряда путем отбрасывания первых его членов, называют остатком ряда и его сумму обозначают .

Примеры числовых рядов:

1. Ряд из членов геометрической прогрессии: , сходится при 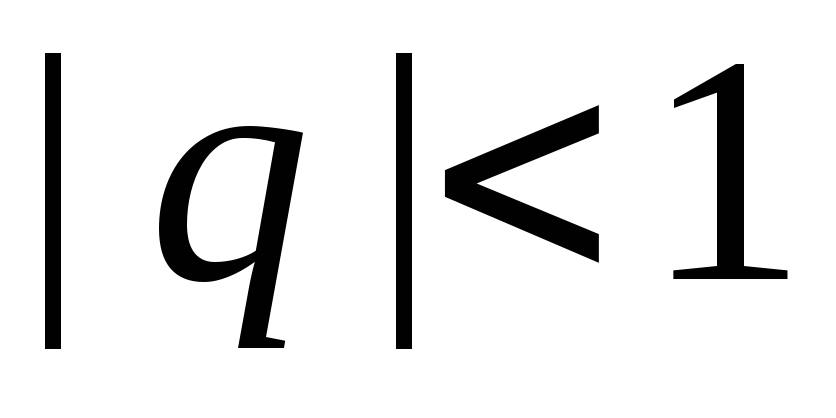, при этом, и расходится при .

2. Обобщенный гармонический ряд: сходится при и расходится при .

Свойства сходящихся рядов:

1. Если ряд сходится, то сходится и любой из его остатков.

Следствие. Все остатки ряда сходятся и расходятся одновременно.

2. Если ряд 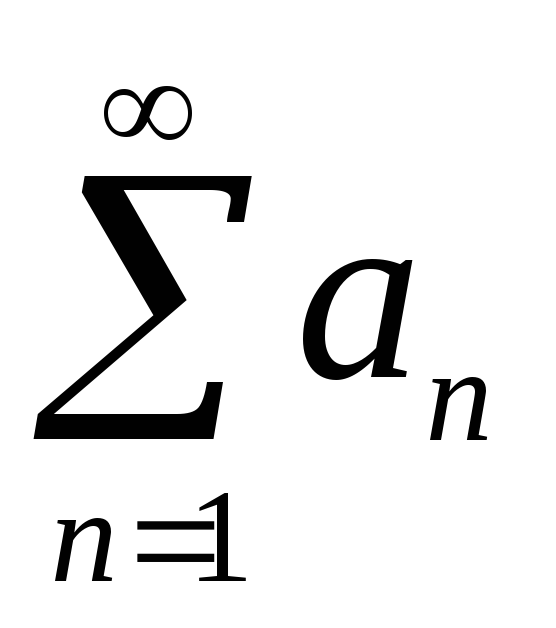сходится, то последовательность , где 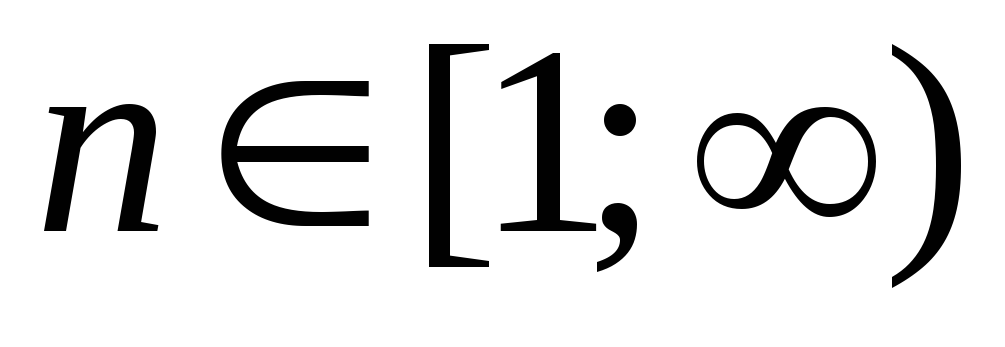стремится к нулю при : .

3. Если в ряде 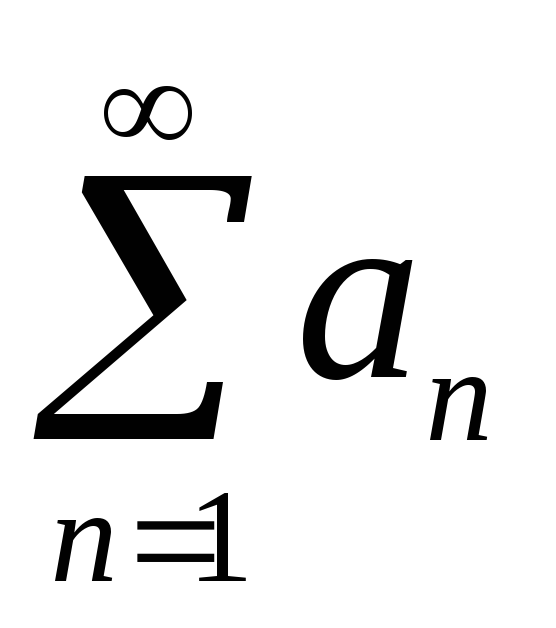отбросить конечное число членов или заменить конечное число членов другими, то это не отразится на его сходимости или расходимости.

4. Отбрасывание членов, равных нулю, не влияет на сходимость или расходимость ряда, а в случае сходимости не изменяет сумму ряда.

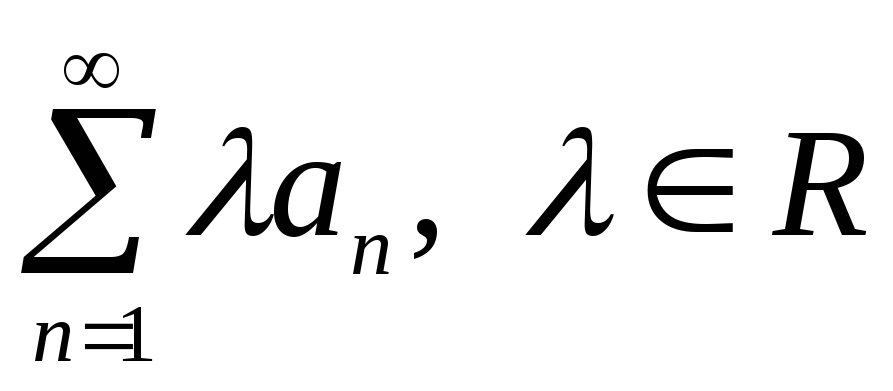5. Если ряд сходится и имеет сумму , то ряд также сходится и имеет сумму : .

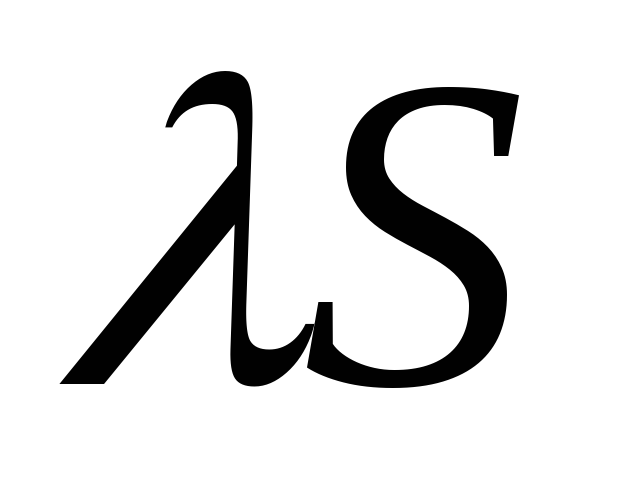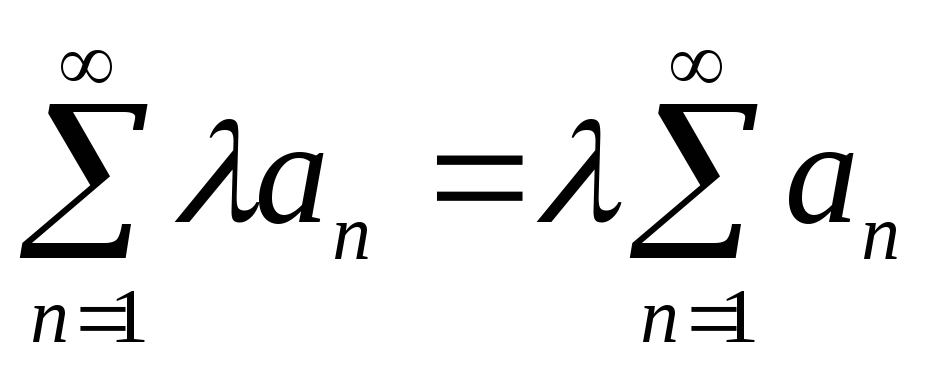6. Если ряды и сходятся и имеют суммы равные и соответственно, то ряд 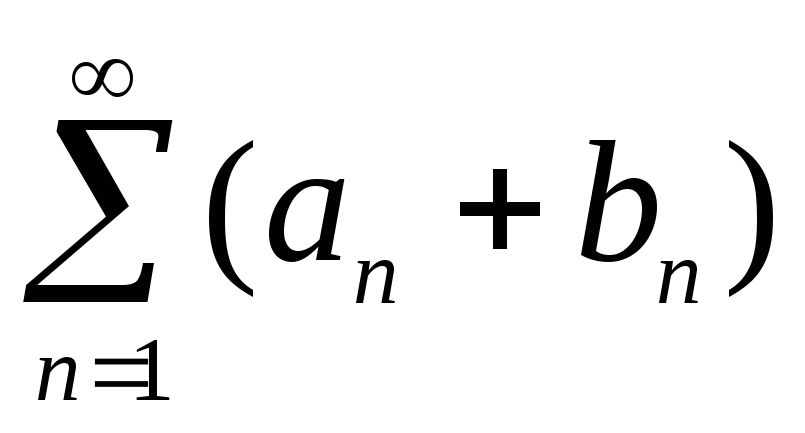также сходится и его сумма равна : .

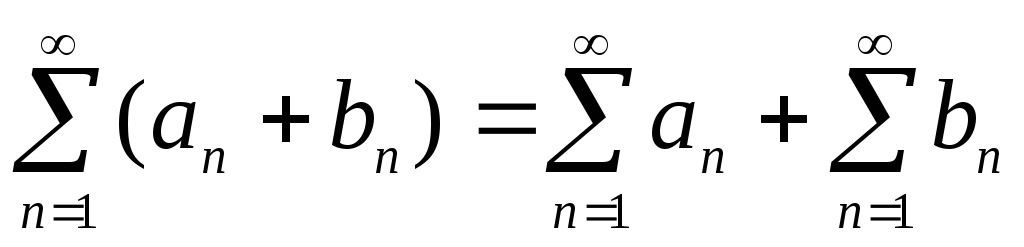7. Если каждый член сходящегося ряда не превышает соответствующий член 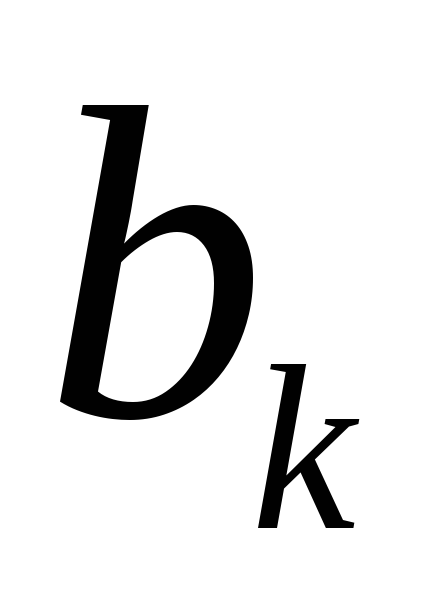сходящегося ряда 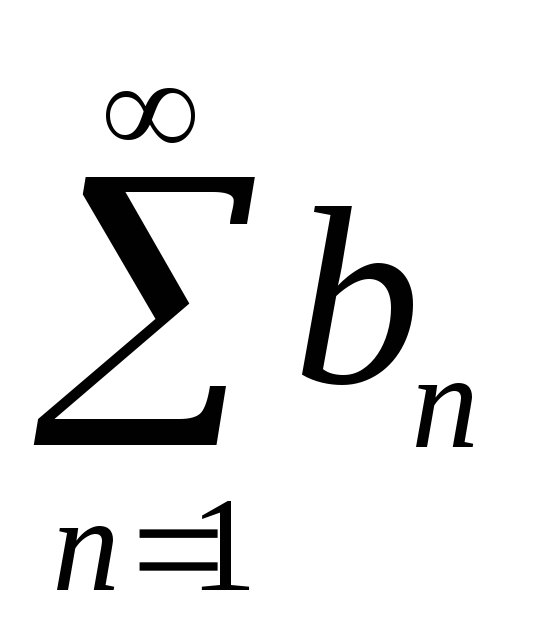, то сумма ряда не превышает сумму ряда , т.е. .

Критерий Коши сходимости числового ряда. Числовой ряд сходится тогда и только тогда, когда для любого найдется такой номер , зависящий от , что для всех и любого натурального выполняется неравенство: .

Пример. Найти сумму ряда: .

Решение: Члены ряда являются членами геометрической прогрессии, где , тогда

,

.

Ответ: Сумма ряда равна 2/3.

Пример. Доказать расходимость ряда: .

Доказательство: Применим необходимый признак сходимости

,

следовательно, ряд расходится. Доказано.

Ряды с положительными членами.

Ряд , в котором все называется положительным.

Общий признак сходимости. Для того, чтобы положительный ряд сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху.

Признаки сравнения положительных рядов. Пусть даны два ряда: и . Тогда:

1. Если при всех , то из сходимости ряда следует сходимость ряда , а из расходимости ряда следует расходимость ряда .

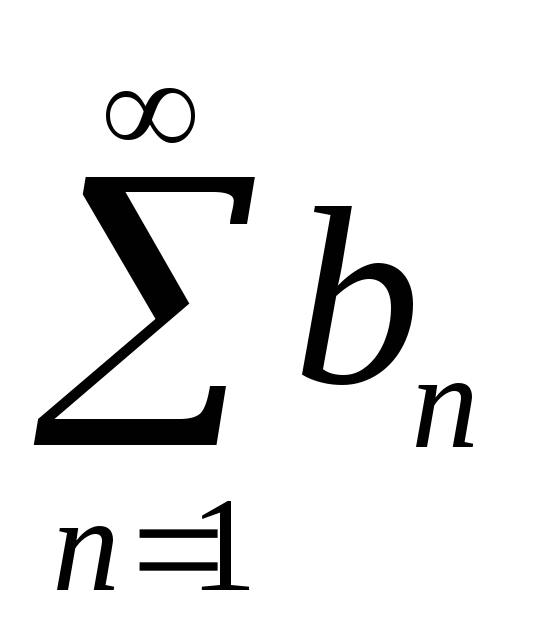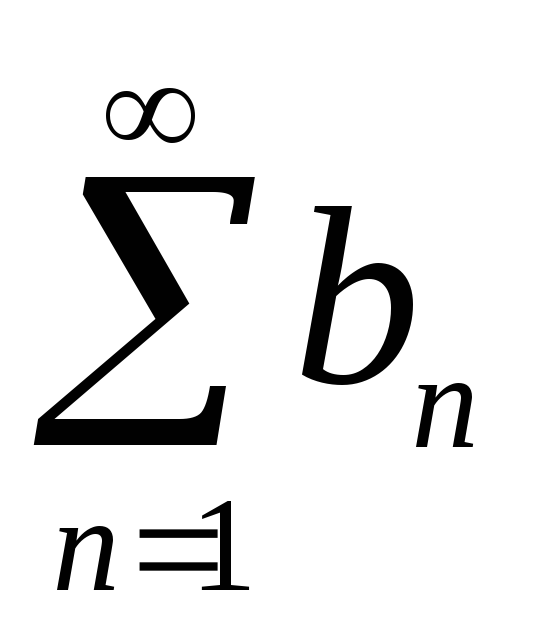2. Если существует не равный нулю и конечный, то ряды и сходятся и расходятся одновременно.

3. Если 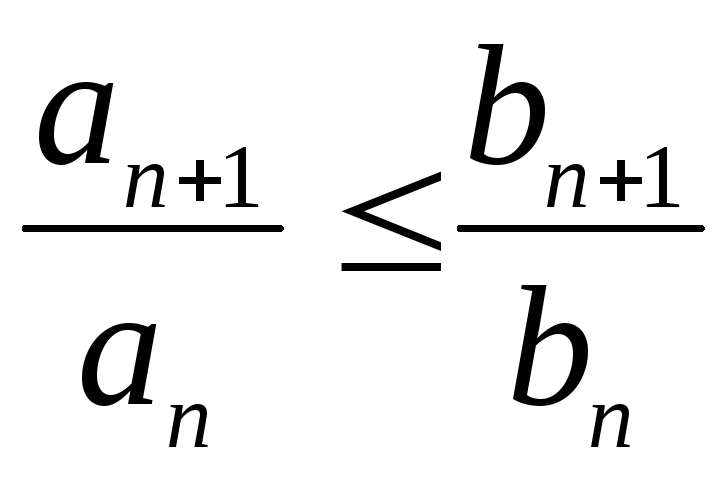при всех 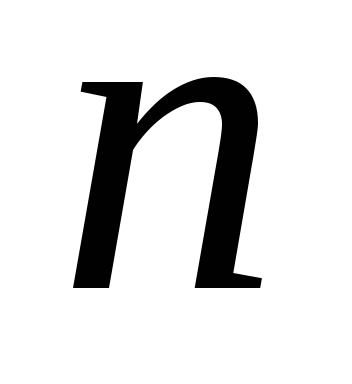, то из сходимости ряда 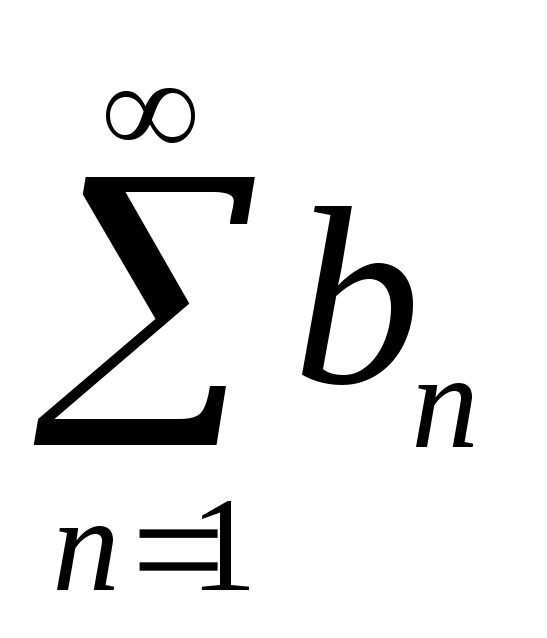вытекает сходимость ряда 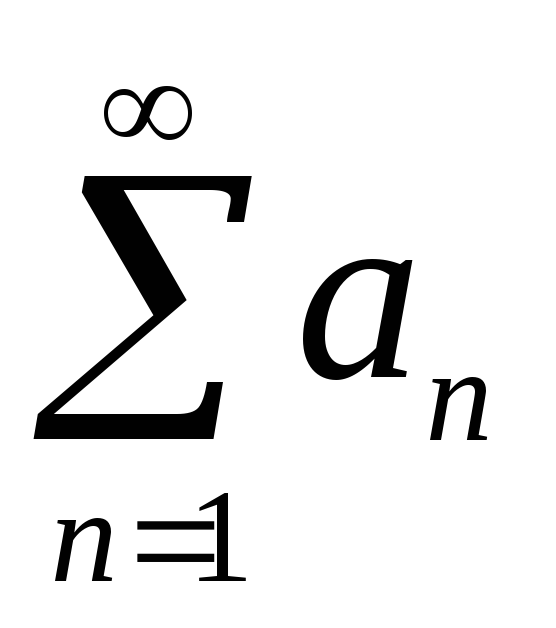, а из расходимости ряда вытекает расходимость ряда .

Признак Даламбера. Пусть для положительного ряда существует . Тогда при ряд сходится; при ряд расходится; при требуются дополнительные исследования.

Интегральный признак Коши. Пусть члены ряда положительны и убывают, т.е. и пусть  непрерывная, положительная, убывающая функция, определенная при , такая что . Тогда интеграл и ряд сходятся и расходятся одновременно.

Пример. Исследовать на сходимость ряды:

А) ;	Б)
В)

Решение:

А) Воспользуемся признаком сравнения. Сравним данный ряд с сходящимся рядом: , который является геометрической прогрессией с множителем . Сравниваем: . Так как больший ряд сходится, следовательно, и данный ряд тоже сходится.

Б) Будем использовать признак Даламбера.

.

Получили , следовательно ряд сходится.

В) Воспользуемся интегральным признаком Коши. Для этого рассмотрим интеграл

.

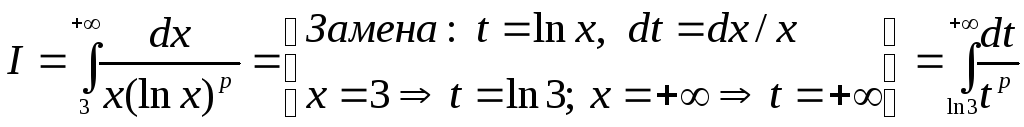Если , то , следовательно, ряд расходится.

Если , то получаем  это гармонический ряд, при ряд сходится, при ряд расходится.

Знакопеременные ряды.

Ряд называется знакопеременным, если он имеет бесконечное число как положительных, так и отрицательных членов.

Знакопеременный ряд называется абсолютно сходящимся, если сходится абсолютный ряд . Сходимость ряда влечет за собой сходимость ряда .

Знакопеременный ряд называется условно сходящимся, если абсолютный ряд расходится, а исходный  сходится.

Числовой ряд называется знакочередующимся, если для любого члены ряда и имеют различные знаки, т.е. .

Признак Лейбница. Пусть для знакочередующегося ряда выполнены условия: 1. Последовательность является не возрастающей: . 2. . Тогда ряд сходится, а его сумма не превосходит первого члена: .

Теорема. Если ряд сходится абсолютно к сумме , то члены ряда можно переставлять в любом порядке, и сумма переставленного ряда также будет равна .

Свойство. Члены сходящегося ряда можно группировать произвольно, при этом сумма ряда не изменяется.

Теорема Римана. Если ряд сходится условно, то путем соответствующей перестановки его членов можно получить ряд с наперед заданным значением суммы (при этом не исключается ±∞).

Пример. Исследовать ряд на абсолютную и условную сходимость:

1. ;

2. .

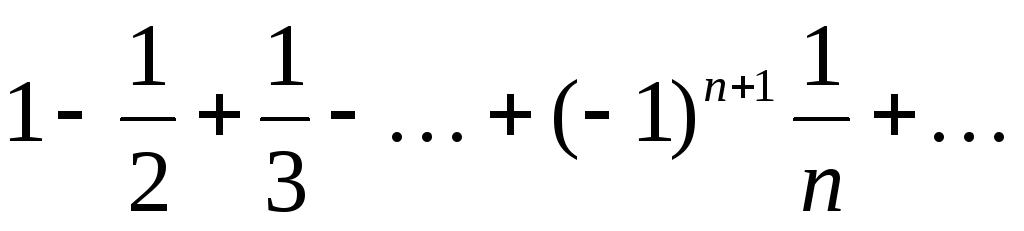Решение: Для исследования на абсолютную сходимость ряда можно использовать признаки сходимости положительных рядов.

1. Составим ряд из модулей членов данного ряда:

.

Применим для данного ряда признак сходимости Коши:

.

Откуда следует, что ряд сходится абсолютно.

2. Применим признак Лейбница.

1. Последовательность не возрастает .

2. .

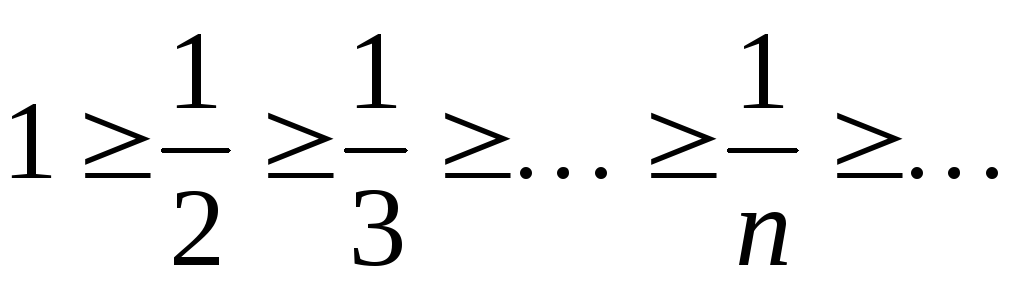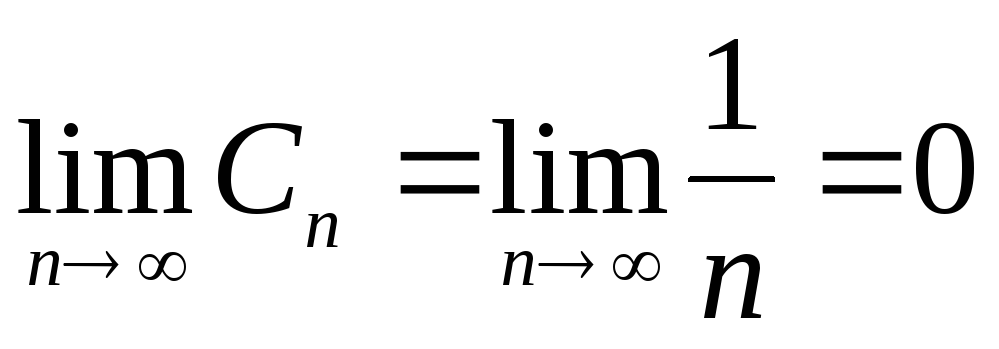Следовательно, ряд сходится.

Рассмотрим ряд составленный из модулей:  это гармонический ряд и он расходится.

Получим, что данный ряд сходится условно.