
- •Лекція 1 Вступ. Основні поняття і визначення
- •Лекція 2 Теорія кіл постійного струму. Режими і закони
- •Лекція 3 Теорія кіл постійного струму. Розрахунок розгалужених кіл
- •Аналіз електричних кіл при гармонічних діях Лекція 4 Синусоїдний струм: моделі та аналіз
- •Лекція 5 Аналіз простих кіл змінного струму
- •Лекція 6 Аналіз простих кіл змінного струму II
- •Частотні характеристики електричних кіл. Резонансні кола Лекція 7 Частотні характеристики кіл
- •Лекція 8 Послідовний коливальний контур
- •Лекція 9 Паралельний коливальний контур
- •Лекція 10 Зв’язані коливальні контури
- •Лекція 11 Електричні фільтри
- •Часові методи аналізу електричних кіл Лекція 12 Класичний метод аналізу перехідних процесів у електричних колах першого порядку
- •Лекція 13 Класичний метод аналізу перехідних процесів у електричних колах другого порядку
- •Лекція 14 Метод інтеграла згортки
- •Список літератури
Частотні характеристики електричних кіл. Резонансні кола Лекція 7 Частотні характеристики кіл
Комплексні функції кіл та їхній зв’язок з параметрами ЕК.
Частотні характеристики кіл, їх властивості та розрахунок.
Як уже відомо, комплексний метод аналізу КЗС полягає у поданні часових синусоїдних функцій через експоненційні функції уявної частоти
 :
:

Застосування
функції
 дозволяє
ввести поняття комплексної функції
(КФ) кола. Це поняття служить для опису
лінійних кіл, які не містять у собі
незалежних джерел енергії.
дозволяє
ввести поняття комплексної функції
(КФ) кола. Це поняття служить для опису
лінійних кіл, які не містять у собі
незалежних джерел енергії.
Сигнал
 на виході лінійного кола і сигнал
на виході лінійного кола і сигнал на
його вході зв’язані лінійним диференційним
рівнянням виду:
на
його вході зв’язані лінійним диференційним
рівнянням виду:
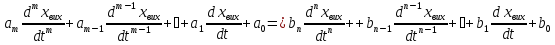 ,
(7.1)
,
(7.1)
де
 - дійсні коефіцієнти, які залежать лише
від параметрів кола і його схеми.
- дійсні коефіцієнти, які залежать лише
від параметрів кола і його схеми.
Застосуємо до рівняння (7.1) комплексний метод. Здійснивши перехід із дійсної, часової області оригіналів до комплексної площини зображень для вхідної і вихідної синусоїдних величин:
 ,
,
і
урахувавши, що операція диференціювання
у часовій області заміняється у
комплексній області множення на
 ,
одержимо наступне рівняння:
,
одержимо наступне рівняння:

 (7.2)
(7.2)
Комплексною функцією кола називається відношення комплексних зображень реакції кола і його вхідної дії:


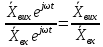

 (7.3)
(7.3)
Порядок
ЕК і його КФ визначається найвищим
степенем при
 у знаменнику виразу (7.3) – поліномі
у знаменнику виразу (7.3) – поліномі .
.
КФ дозволяє легко знайти зображення вихідного сигналу, якщо відоме зображення вхідного сигналу:
 (7.4)
(7.4)
Нехай
ЕК представлено у вигляді пасивного
чотириполюсника рис. 7.1. Таке подання
уможливлює проведення класифікації
комплексних функцій кола. На вхідних
затискачах 1-1’ діють напруги
 і
струм
і
струм
 .
На
затискачах 2-2’ окремо виділеного
елемента
.
На
затискачах 2-2’ окремо виділеного
елемента
 схеми
діють напруга
схеми
діють напруга
 і струм
і струм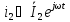 .
.
 Рисунок
7.1
Рисунок
7.1
Комплексні функції кола можуть бути вхідними і передаточними.
Вхідна функція – це відношення зображень струму і напруги, які діють на вхідних затискачах. До таких функцій належить вхідний опір і вхідна провідність.



 (7.5)
(7.5)
Передаточна функція – це відношення зображень струмів і напруг, які діють на різних парах затискачів. До таких функцій належать: комплексні передаточні функції, або коефіцієнти передачі за напругою і струмом:

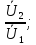

 ;
(7.6)
;
(7.6)
Передаточні опори:



 ;
(7.7)
;
(7.7)
Передаточні провідності:

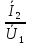

 (7.8)
(7.8)
Розглянемо
зв’язок КФ кола з його параметрами
детальніше. Нехай дано схему ЕК рис.
7.2. На ній
 - реальні джерела вхідного сигналу. На
вході ЕК діють напруга
- реальні джерела вхідного сигналу. На
вході ЕК діють напруга і
струм
і
струм ,
а на виході, тобто на будь-якому елементі
,
а на виході, тобто на будь-якому елементі – напруга
– напруга
 і
струм
і
струм
 .
.
 Рисунок
7.2
Рисунок
7.2
Знайдемо відношення між цими напругами та струмами, скориставшись методом контурних струмів. Вважаючи k-й і l-й контури зовнішніми, запишемо систему рівнянь за МКС:
 (7.9)
(7.9)
де
 -
контурні
опори,
-
контурні
опори,
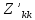 - сума опорів елементівk-го
контуру без урахування внутрішнього
опору джерела
- сума опорів елементівk-го
контуру без урахування внутрішнього
опору джерела
 - контурний опірk-го
контуру;
- контурний опірk-го
контуру;

 -
контурні струми. Із системи рівнянь
(7.9) виключені параметри джерела сигналу.
-
контурні струми. Із системи рівнянь
(7.9) виключені параметри джерела сигналу.
Розв’язок
системи відносно вихідного струму
 (див. лекцію 3):
(див. лекцію 3):


 ,
(7.10)
,
(7.10)
де
Δ – детермінант системи (7.9); Δkl
– алгебраїчне
доповнення елемента
 .
.
Аналогічно одержимо розв’язок відносно струму на виході:



 (7.11)
(7.11)
Вхідні і передаточні функції ЕК рис. 7.2 знаходимо з урахуванням формул (7.10) і (7.11):
Вхідна провідність:
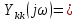
 ;
(7.12)
;
(7.12)
Передаточні провідність і опір:

 ;
;

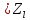
 ; (7.13)
; (7.13)
Коефіцієнт передачі за напругою і струмом:



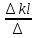

 (7.14)
(7.14)
Детермінанти
 -
являють собою суму добутків контурних
опорів, наприклад:
-
являють собою суму добутків контурних
опорів, наприклад:
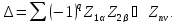
Будь-який
контурний опір у загальному випадку є
раціональною функцією уявної частоті
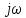 :
:

і
тому детермінанти є раціональними функціями, а відтак усі
перераховані КФ (7.12) – (7.14) є раціональними
функціями змінної
є раціональними функціями, а відтак усі
перераховані КФ (7.12) – (7.14) є раціональними
функціями змінної і можуть бути подані у вигляді раціонального
дробу (7.3) з дійсними коефіцієнтами.
Важливими є те, що всі коефіцієнти
чисельника
і можуть бути подані у вигляді раціонального
дробу (7.3) з дійсними коефіцієнтами.
Важливими є те, що всі коефіцієнти
чисельника і знаменника
і знаменника цього дробу є величинами дійсними,
оскількивони
залежать лише від схеми ЕК і визначаються
його параметрами
цього дробу є величинами дійсними,
оскількивони
залежать лише від схеми ЕК і визначаються
його параметрами

Таким
чином, КФ кола (вхідні і передаточні) не
залежать від вибору визначальних величин
(контурних струмів, вузлових потенціалів)
або вибору незалежних контурів і вузлів.
Вони однозначно визначаються виключно
схемою кола і його параметрами
 Інакше
кажучи, схема і параметри кола зумовлюють
той чи інший характер частотної залежності
КФ, яка породжена присутністю реактивних
елементів у колі.
Інакше
кажучи, схема і параметри кола зумовлюють
той чи інший характер частотної залежності
КФ, яка породжена присутністю реактивних
елементів у колі.
Частотні характеристики ЕК є компонентами комплексних функцій. Нехай маємо КФ кола:
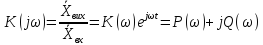 (7.15)
(7.15)
Тут функція
 (7.16)
(7.16)
Модуль
КФ, який називається амплітудно-частотною
характеристикою (АЧХ) кола. Величина
 - це відношення амплітуди вихідного
сигналу до амплітуди вхідного сигналу.
- це відношення амплітуди вихідного
сигналу до амплітуди вхідного сигналу.
Функція
 (7.17)
(7.17)
визначає зсув за фазою реакції кола відносно вхідної дії і називається фазочастотною характеристикою (ФЧХ) кола.
Функція
 (7.18)
(7.18)
це дійсна частина КФ кола і називається дійсною частотною характеристикою (ДЧХ) кола.
Функція
 (7.19)
(7.19)
це уявна частина КФ кола і називається уявною частотною характеристикою (УЧХ) кола.
Частотні
характеристики описують властивості
ЕК при дії на них синусоїдних сигналів.
Вони можуть легко бути виміряні в
експериментальний спосіб. За їх допомогою
можна визначити реакцію кола на задану
дію будь-якої частоти, а також аналізувати
важливі особливості застосування кола.
Так, АЧХ, зображена на рис. 7.3, характеризую
ЕК, яке має властивості пропускати
сигнали тільки в діапазоні частот від
 до
до .
Таке коло може бути застосоване як
смуговій фільтр. Ця АЧХ дозволяє оцінити
такі якісні показники кола, як рівномірність
характеристики у межах смуги пропускання
(діапазон частот від
.
Таке коло може бути застосоване як
смуговій фільтр. Ця АЧХ дозволяє оцінити
такі якісні показники кола, як рівномірність
характеристики у межах смуги пропускання
(діапазон частот від до
до ),
затухання поза смугою пропускання
(частоти менші за
),
затухання поза смугою пропускання
(частоти менші за та більші за
та більші за ),
крутизну характеристики на межах смуги
пропускання. До того ж можна кількісно
визначити граничні частоти
),
крутизну характеристики на межах смуги
пропускання. До того ж можна кількісно
визначити граничні частоти ,
, ,
смугу пропускання
,
смугу пропускання тощо.
тощо.

Рисунок 7.3
Розглянемо деякі приклади визначення частотних характеристик ЕК:
Фільтр верхніх частот (рис. 7.4) КФ RC кола:

 (7.20)
(7.20)
Уведемо
позначення
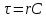 ,
яке називаєтьсястала
часу
кола. Одержимо:
,
яке називаєтьсястала
часу
кола. Одержимо:
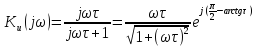

 -
АЧХ
RC
кола.
-
АЧХ
RC
кола.
 -
ФЧХ
RC
кола.
-
ФЧХ
RC
кола.
АЧХ і ФЧХ показані на рис. 7.4 б. Якщо КФ подати у алгебраїчній формі
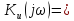
 ,
,
то отримаємо ДЧХ і УЧХ (рис. 7.4 в):


Рисунок 7.4
Фільтр нижніх частот (рис. 7.5)

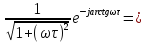
 (7.21)
(7.21)

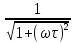 –АЧХ
–АЧХ
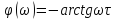 -
ФЧХ
-
ФЧХ
АЧХ і ФЧХ показані на рис. 7.5 б.

 -
ДЧХ
-
ДЧХ

 -
УЧХ.
-
УЧХ.
ДЧХ і УЧХ показані на рис. 7.5 в.
Окрім rC - кіл, існують ще й rL - кола, які виконують такі ж самі функції щодо обробки сигналів. Ці кола показані на рис. 7.6 а,б.
Оцінимо їх КФ. Для схеми рис. 7.6 а:

де

 - стала
часу кола.
- стала
часу кола.
Для схеми рис. 7.6 б:

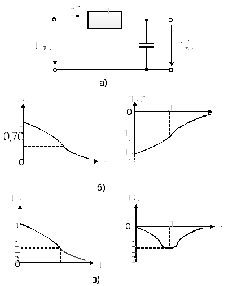
Рисунок 7.5
 Рисунок
7.6
Рисунок
7.6
Отримані вирази комплексних функцій rL – кіл рис. 7.6 свідчить про те, що частотні характеристики rL – кіл збігаються з частотними характеристиками rС – кіл, причому схема рис. 7.6 а є фільтром верхніх частот, дуальним до схеми рис. 7.5 а, а схема рис. 7.6 б є фільтром нижніх частот, дуальним до фільтру рис. 7.5 б.
Розглянуті приклади підтверджують теоретичні положення про властивості комплексних функцій ЕК. Ці властивості наступні:
 –властивість
спряженої симетрії;
–властивість
спряженої симетрії;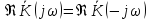 –властивість
парності ДЧХ;
–властивість
парності ДЧХ; –властивість
непарності
УЧХ;
–властивість
непарності
УЧХ; –парність
АЧХ;
–парність
АЧХ;
 –непарність
ФЧХ.
–непарність
ФЧХ.
