Лекція 5 Аналіз простих кіл змінного струму

1. Коло змінного струму з одним пасивним елементом.

2. КЗС з послідовним і паралельним з’єднанням елементів r, L,C.

1. КЗС з активним опором r

Рисунок 5.1

Якщо прикласти до опору r напругу

,

по колу рис. 5.1 а потече струм

де ;

В КЗС з одним пасивним елементом – активним опором r – напруга і струм збігаються за фазою: (див. рис. 5.1 б).

Комплексний опір

Комплексна провідність

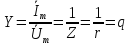
КЗС з індуктивністю L

Якщо прикласти напругу до котушки з індуктивністюL, то через неї потече струм

Рисунок 5.2

Струм наводить у котушціL ЕРС самоіндукції , яка врівноважує прикладену напругу

(5.1)

Підставивши до формули (5.1) вираз для струму , виконавши операцію диференціювання, одержимо:

де ;.

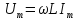Зсув фаз між напругою і струмом у колі з індуктивністю (рис. 5.2 а) дорівнює , тобто у індуктивності відстає за фазою навід прикладеної напруги (рис. 5.2 б).

Комплексний опір кола з індуктивністю:

(5.2)

де - індуктивний опір.

Фізичний сенс індуктивного опору полягає у тому, що протіканню струму через котушку перешкоджає ЕРС самоіндукції, яка виникає у котушці, породжена струмом і спрямована на зустріч прикладеній до котушки напрузіІндуктивний опір є лінійною функцією частоти (рис. 5.3).

Рисунок 5.3

Комплексна провідність:

(5.3)

де – індуктивна провідність.

Чисто уявний характер комплексних опору та провідності кола з індуктивністю вказує на її чисто реактивний характер.

КЗС з ємністю С Рисунок 5.4

Якщо до конденсатора С (рис. 5.4 а) прикласти напругу , то у колі потече струм

де .

Зсув фаз між напругою і струмом у колі з ємністю С (рис. 4.5 а) дорівнює , тобто струм через ємність випереджає прикладену напругу за фазою на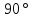(рис. 4.5 б).

Комплексний опір кола з ємністю:

(5.4)

де 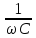– ємнісний опір.

Фізичний сенс ємнісного опору полягає у тому, що чим більше частота струму, тим частіше відбувається перезаряд ємності С, а відтак тим менший її реактивний опір. Адже ємність має менший опір щодо струму заряду саме на початку заряду. Цей ефект посилюється у разі збільшення самої ємності. Залежність ємнісного опору від частоти графічно показана на рис. 5.5.

Рисунок 5.5

(5.5)

де - ємнісна провідність.

Дане коло, подібно до попереднього, має чисто уявний характер комплексного опору (провідності), а відтак є чисто реактивним.

2. КЗС із послідовним з’єднанням елементів r, L,C

Якщо до кола рис. 5.6 прикласти напругу , то у колі потече струм

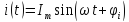
За ІІ законом Кірхгофа для миттєвих значень напруг

де

Рисунок 5.6

За ІІ законом Кірхгофа для комплексних значень напруг

(5.6)

оскільки

Комплексний опір кола:

(5.7)

де – повний опір.

Нехай частота напруги 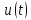змінюється, а відтак змінюються реактивні опори кола. Розглянемо три випадки:

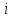1. Струм відстає за фазою від напруги на деякий кут. Коло маєіндуктивний характер (див. векторну діаграму рис. 5.7 а);

2. Струм випереджає за фазою напругу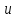на деякий кут. Коло маєємнісний характер (рис. 5.7 б).

3. Опір кола чисто активний. При цьому, оскільки , то струм у колі збільшується в порівнянні з попередніми випадками. Це явище називається резонансом напруг (див. векторну діаграму рис. 5.7 в).

Рисунок 5.7

Комплексна провідність r, L,C:

де .

КЗС із паралельним з’єднанням елементів r, L, C

Нехай до входу кола рис. 5.8 прикладена напруга . За І законом Кірхгофа:

де

За І законом Кірхгофа для комплексних значень струмів:

Комплексна провідність кола:

де .

Рисунок 5.8

Характер кола рис. 5.8. залежить від співвідношення реактивних провідностей. Три випадки в залежності від частоти вхідної напруги:

1. Струм відстає від прикладеної напруги . Коло має індуктивний характер (див. діаграму рис. 5.9 а).

2. Струм випереджає прикладену напругу. Коло має ємнісний характер.

3. Провідність кола чисто активна 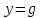. При цьому , оскільки , то струм у нерозгалуженій частині кола стає значно меншим, ніж у попередніх випадках. Це явище називається резонансом струмів (див. векторну діаграму рис 5.9 в).

Рисунок 5.9

Комплексний опір кола рис. 5.8

де .

Висновки з лекції:

1. Опори (провідності) реактивних елементів є суттєво частотозалежними:

2. Характер КЗС (індуктивний, ємнісний, чисто активний) залежить від частоти вхідної дії на коло ( якщо КЗС є у загальному випадку комплексною).

3. При деякій частоті вхідної дії настає рівність

КЗС набуває активного характеру , і в ньому виникає або резонанс напруг при послідовному з’єднанні елементів r, L, C – коли напруга на елементах на багато разів перевищує ЕРС джерела живлення (послідовний резонанс), або резонанс струмів при паралельному з’єднанні елементів r, L, C – коли струми у гілках набагато перевищують струм у нерозгалуженій частині схеми (паралельний резонанс).