
- •Лекція 1 Вступ. Основні поняття і визначення
- •Лекція 2 Теорія кіл постійного струму. Режими і закони
- •Лекція 3 Теорія кіл постійного струму. Розрахунок розгалужених кіл
- •Аналіз електричних кіл при гармонічних діях Лекція 4 Синусоїдний струм: моделі та аналіз
- •Лекція 5 Аналіз простих кіл змінного струму
- •Лекція 6 Аналіз простих кіл змінного струму II
- •Частотні характеристики електричних кіл. Резонансні кола Лекція 7 Частотні характеристики кіл
- •Лекція 8 Послідовний коливальний контур
- •Лекція 9 Паралельний коливальний контур
- •Лекція 10 Зв’язані коливальні контури
- •Лекція 11 Електричні фільтри
- •Часові методи аналізу електричних кіл Лекція 12 Класичний метод аналізу перехідних процесів у електричних колах першого порядку
- •Лекція 13 Класичний метод аналізу перехідних процесів у електричних колах другого порядку
- •Лекція 14 Метод інтеграла згортки
- •Список літератури
Часові методи аналізу електричних кіл Лекція 12 Класичний метод аналізу перехідних процесів у електричних колах першого порядку
Перехідні процеси у ЕК та класичний підхід до їх аналізу.
Вільні напруги і струми у простих ЕК.
Перехідні процеси у простих ЕК з джерелом постійної напруги.
Перехідні процеси у простих ЕК з джерелом синусоїдної напруги.
Перехідні процеси у розгалужених колах першого порядку.
Розрізнення стаціонарного і перехідного режимів у ЕК викладається у лекції 2 (1-е питання). Досі аналіз ЕК ми здійснювали виключно для умов стаціонарного режиму. Наступні три лекції стосуються нестаціонарних режимів ЕК, тобто перехідних процесів (ПП). ПП виникають в колі при:
підключенні – відключенні джерел енергії від кіл;
стрибкоподібній зміні схеми кола;
стрибкоподібній зміні параметрів елементів кола.
Усі
ці зміни можна описувати через комутацію
(замикання і розмикання). Тривалість
комутації нескінченно мала,
 ,
тобто комутація відбувається миттєво.
Момент комутації
,
тобто комутація відбувається миттєво.
Момент комутації є
початком відліку часу. Тоді
є
початком відліку часу. Тоді
 - це момент, що безпосередньо передує
моменту комутації, а
- це момент, що безпосередньо передує
моменту комутації, а - момент, що безпосередньо слідує за
моментом комутації.
- момент, що безпосередньо слідує за
моментом комутації.
В
ЕК, які не містять в собі енергоємних
елементів (L
і
C),
після комутації установлюється новий
стаціонарний режим одразу і миттєво. В
таких ЕК перехідні процеси відсутні. У
колах з індуктивностями і ємностями ПП
тривають певний час, оскільки електрична
енергія конденсаторів

 і магнітна енергія індуктивних котушок
і магнітна енергія індуктивних котушок
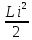 не можуть змінюватися стрибкоподібно
внаслідок тяглості (неперервності)
енергії у часі. Практично це означає
неможливість стрибків струмів в
індуктивностях і напруг на ємностях.
не можуть змінюватися стрибкоподібно
внаслідок тяглості (неперервності)
енергії у часі. Практично це означає
неможливість стрибків струмів в
індуктивностях і напруг на ємностях.
Це засвідчують наступні закони комутації ЕК:
 ;
;
 (12.1)
(12.1)
Класичний метод аналізу ПП в електричних колах має наступний алгоритм:
Складається система рівнянь миттєвих значень струмів
 та
напруг
та
напруг
 (за
допомогою одного з вивчених методів –
МРК, МКС або МВП). При цьому застосовують
співвідношення:
(за
допомогою одного з вивчених методів –
МРК, МКС або МВП). При цьому застосовують
співвідношення:
 (12.2)
(12.2)
В одержаній системі рівнянь вибирається основна змінна. Через виключення інших змінних із системи одержують одне рівняння відносно основної лише змінної. Для лінійних ЕК, що містять елементи
 ,
це рівняння є інтегро - диференційним.
,
це рівняння є інтегро - диференційним.Через повторне диференціювання з останнього рівняння можна одержати лінійне неоднорідне диференційне рівняння з постійними коефіцієнтами виду:

 ,
(12.3)
,
(12.3)
де
 і
і -
постійні коефіцієнти, що залежать від
схеми ЕК і параметрів його елементів;
-
постійні коефіцієнти, що залежать від
схеми ЕК і параметрів його елементів; - вихідна величина (напруга, струм і
т.д.);
- вихідна величина (напруга, струм і
т.д.); - зовнішня дія на коло (джерело ЕРС або
струму). Порядок вищої похідної рівняння
визначає порядок кола.
- зовнішня дія на коло (джерело ЕРС або
струму). Порядок вищої похідної рівняння
визначає порядок кола.
Розв’язок рівняння (12.3) шукають у вигляді:
 (12.4)
(12.4)
де
 - вільна складова – загальний розв’язок
однорідного диференційного рівняння:
- вільна складова – загальний розв’язок
однорідного диференційного рівняння:
 (12.5)
(12.5)
 -
примушена складова – частковий розв’язок
рівняння (12.3) з ненульовою правою
частиною.
-
примушена складова – частковий розв’язок
рівняння (12.3) з ненульовою правою
частиною.
Складова
 - це вільні електричні струми або напруги.
Вони дорівнюють різниці перехідних і
усталених струмів або напруг. Складова
- це вільні електричні струми або напруги.
Вони дорівнюють різниці перехідних і
усталених струмів або напруг. Складова - характеризує процес, що виникає у ЕК
під впливом зовнішньої дії по закінченні
ПП, тобто під впливом ЕРС або струму
джерел (коли
- характеризує процес, що виникає у ЕК
під впливом зовнішньої дії по закінченні
ПП, тобто під впливом ЕРС або струму
джерел (коли ).
).
Розв’язок однорідного диференційного рівняння (12.5) має вид:
 (12.6)
(12.6)
де
 - корені характеристичного рівняння:
- корені характеристичного рівняння:
 (12.7)
(12.7)
 –сталі
інтегрування.
–сталі
інтегрування.
Корені
 у пасивних електричних кіл або дійсні
від’ємні, або комплексні з від’ємною
дійсною частиною, а відтак
у пасивних електричних кіл або дійсні
від’ємні, або комплексні з від’ємною
дійсною частиною, а відтак .
Фізично це означає, що вільний процес
перебігає за рахунок енергії, накопиченої
в реактивних елементах кола, а ця енергія
з бігом часу витрачається на незворотні
втрати в активних опорах. Сталі
інтегрування
.
Фізично це означає, що вільний процес
перебігає за рахунок енергії, накопиченої
в реактивних елементах кола, а ця енергія
з бігом часу витрачається на незворотні
втрати в активних опорах. Сталі
інтегрування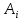 визначаються за початковими умовами –
значеннями
визначаються за початковими умовами –
значеннями і
і
 ,
тобто в момент безпосередньо після
комутації. Для визначення початкових
умов застосовують закони комутації
(12.1). Якщо в момент комутації
,
тобто в момент безпосередньо після
комутації. Для визначення початкових
умов застосовують закони комутації
(12.1). Якщо в момент комутації і
і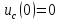 ,
тобто індуктивність еквівалентна
розриву кола, а ємність – короткому
замиканню, то такі початкові умови є
нульовими. При
,
тобто індуктивність еквівалентна
розриву кола, а ємність – короткому
замиканню, то такі початкові умови є
нульовими. При і
і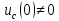 у колі мають місце ненульові початкові
умови.
у колі мають місце ненульові початкові
умови.
Закони
комутації (12.1) стосуються виключно
струмів індуктивності і напруг ємності,
а відтак у момент комутації
 і
і можуть змінюватися стрибкоподібно,
тобто
можуть змінюватися стрибкоподібно,
тобто ;
; .
.
У ЕК першого порядку рівняння (12.3) має вид:
 (12.8)
(12.8)
Примушена
складова розв’язку рівняння (12.4), яка
є струмом або напругою в усталеному
режимі, визначається безпосередньо із
схеми кола при
 .
Вільна
складова шукається у вигляді:
.
Вільна
складова шукається у вигляді:
 ,
(12.9)
,
(12.9)
де
 – корінь характеристичного рівняння
– корінь характеристичного рівняння ;
; – стала інтегрування, що визначається
за початковими умовами кола.
– стала інтегрування, що визначається
за початковими умовами кола.
Нехай
маємо коло першого порядку рис. 12.1а. При
розмиканні ключа К в ізольованому від
зовнішніх джерел
 контурі (рис. 12.1б) за рахунок енергії,
запасеної у магнітному полі елемента
контурі (рис. 12.1б) за рахунок енергії,
запасеної у магнітному полі елемента ,
виникають вільні напруги і струм.
,
виникають вільні напруги і струм.

Рисунок 12.1
Для
ізольованого
 контуру за ІІ законом Кірхгофа
контуру за ІІ законом Кірхгофа ,
або з урахуванням (12.2):
,
або з урахуванням (12.2):



 (12.10)
(12.10)
Розв’язок цього однорідного рівняння має вид:
 (12.11)
(12.11)
Із
характеристичного рівняння
 знайдемо
знайдемо



 , де
, де
 –величина,
що має розмірність часу і називається
сталою часу кола. Підставивши
–величина,
що має розмірність часу і називається
сталою часу кола. Підставивши
 у формулу (12.11), одержимо:
у формулу (12.11), одержимо:
 (12.12)
(12.12)
Сталу
інтегрування
 знайдемо з початкових умов, застосовуючи
перший закон комутації:
знайдемо з початкових умов, застосовуючи
перший закон комутації: .
Відтак
при
.
Відтак
при
 одержимо:
одержимо:

Тому остаточно розв’язок рівняння (12.11) буде:
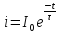 (12.13)
(12.13)
Отже, вільний струм у коли рис. 12.1б зменшується з плином часу за експоненційним законом, як це показано на часовій діаграмі рис. 12.2.

Рисунок 12.2
При
 струм у колі
струм у колі .
Стала
часу
.
Стала
часу
 – це час, протягом якого величина, що
спадає у експоненційний спосіб ,
зменшується в
– це час, протягом якого величина, що
спадає у експоненційний спосіб ,
зменшується в раз. Величина
раз. Величина зв’язана з тривалістю ПП: що більше
зв’язана з тривалістю ПП: що більше ,
то більш тривалим є ПП (рис. 12.2). Практично
ПП вважається завершеним на момент часу
,
то більш тривалим є ПП (рис. 12.2). Практично
ПП вважається завершеним на момент часу ,
коли
,
коли .
.
Вільні
напруги
 і
і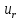 в даному колі змінюються за законом,
аналогічним до закону струму
в даному колі змінюються за законом,
аналогічним до закону струму :
:
 (12.14)
(12.14)
 (12.15)
(12.15)
Про це свідчать і графіки рис. 12.3.

Рисунок 12.3
Підключення джерел ЕРС.
Нехай
маємо коло рис. 12.4. До послідовного
з’єднання елементів
 і
і в момент часу
в момент часу за нульових початкових умов підключається
джерело ЕРС. За ІІ законом Кірхгофа
за нульових початкових умов підключається
джерело ЕРС. За ІІ законом Кірхгофа ,
тобто:
,
тобто:


 (12.16)
(12.16)
Загальний
розв’язок цього неоднорідного рівняння
 .
.

Рисунок 12.4
Примушена
складова

 .
Вільна
складова має вираз (12.12), і тоді загальний
розв’язок рівняння (12.16):
.
Вільна
складова має вираз (12.12), і тоді загальний
розв’язок рівняння (12.16):


 (12.18)
(12.18)
Напруга
на опорі
 змінюється за аналогічним законом:
змінюється за аналогічним законом:
 ,
(12.19)
,
(12.19)
а
напруга на індуктивності
 - за законом:
- за законом:


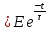 (12.20)
(12.20)
Криві
зміни
 наведені на рис. 12.5
наведені на рис. 12.5

Рисунок 12.5
Струм
 наростає
у колі за експоненційним законом від 0
до
наростає
у колі за експоненційним законом від 0
до

 .
Стала часу
.
Стала часу – це проміжок часу, наприкінці якого
струм зростає до (
– це проміжок часу, наприкінці якого
струм зростає до ( від
свого усталеного значення. Напруга
від
свого усталеного значення. Напруга
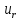 зростає за таким самим законом від 0 до
зростає за таким самим законом від 0 до при
при .
Напруга
.
Напруга
 ,
зумовлена ЕРС самоіндукції, в момент
комутації
,
зумовлена ЕРС самоіндукції, в момент
комутації стрибкоподібно зростає від 0 до
стрибкоподібно зростає від 0 до ,
а потім зменшується за експоненційним
законом до нуля при
,
а потім зменшується за експоненційним
законом до нуля при .
.
Стрибкоподібна зміна схеми кола.
Нехай
дано коло рис. 12.16. Після комутації весь
струм у колі тече через короткозамкнену
перемичку, обминаючи опір
 .
.

Рисунок 12.6
За
ІІ законом Кірхгофа
 або:
або:
 (12.21)
(12.21)
Загальний розв’язок рівняння (12.21):
 (12.22)
(12.22)
де

 – стала часу кола. Оскільки
– стала часу кола. Оскільки

 , то з
виразу (12.22) при
, то з
виразу (12.22) при
 одержимо:
одержимо:
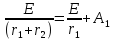
Звідки
 . Підставивши це в формулу (12.22), одержимо:
. Підставивши це в формулу (12.22), одержимо:




 (12.23)
(12.23)
Напруги
 і
і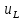 змінюється за законом:
змінюється за законом:

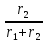
 (12.24)
(12.24)




 (12.25)
(12.25)
Часові діаграми струму і напруг даного кола подані на рис. 12.7.

Рисунок 12.7
Нехай маємо
 - коло першого порядку з джерелом
синусоїдної напруги
- коло першого порядку з джерелом
синусоїдної напруги (рис. 12.8). За ІІ
законом Кірхгофа
(рис. 12.8). За ІІ
законом Кірхгофа
 ,
або:
,
або:
 (12.26)
(12.26)

Рисунок 12.8
Вільна складова напруги на ємності (розв’язок рівняння (12.26) без правої частини):
 ,
(12.27)
,
(12.27)
де
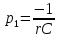 - корінь характеристичного рівняння
- корінь характеристичного рівняння .
Позначивши
.
Позначивши - стала часу кола, одержимо:
- стала часу кола, одержимо:
 (12.28)
(12.28)
Примушена складова напруги на ємності – це синусоїдна функція часу:
 (12.29)
(12.29)
де
 ,
,
 .
.
Загальний розв’язок рівняння (12.26):
 (12.30)
(12.30)
Нульові
початкові умови
 дозволяють знайти сталу
дозволяють знайти сталу :
:
 ,
звідки
,
звідки
 .
.
Тоді остаточний розв’язок рівняння (12.26) набуде вигляду:

 (12.31)
(12.31)
З
цього виразу випливає, що ПП у колі рис.
12.8 залежить від початкової фази
синусоїдної напруги
 .
При
.
При у колі одразу настає усталений режим
без ПП. При
у колі одразу настає усталений режим
без ПП. При вільна напруга на ємності є максимальна
(рис. 12.9), а відтак і ПП у колі буде
тривалішим.
вільна напруга на ємності є максимальна
(рис. 12.9), а відтак і ПП у колі буде
тривалішим.

Рисунок 12.9
При розрахунку перехідних режимів у розгалуженому колі першого порядку, на відміну від простих, нерозгалужених, які розглядались вище, слід при складанні диференційного рівняння кола застосовується не тільки другий, але і перший закони Кірхгофа.
Нехай
маємо коло рис. 12.10. Після комутації в
колі (підключення до кола джерела ЕРС
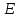 )
на підставі І і ІІ законів Кірхгофа
запишемо систему рівнянь:
)
на підставі І і ІІ законів Кірхгофа
запишемо систему рівнянь:
 (12.32)
(12.32)
Виключивши
із системи струми
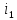 і
і ,
одержимо рівняння для
,
одержимо рівняння для :
:
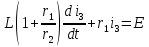
Загальний розв’язок цього рівняння:
 ,
,
де





 ;
;

 .
.
Із
схеми кола рис. 12.10 видно, що в усталеному
режимі гілка з опором
 замикається на коротко гілкою з
індуктивністю
замикається на коротко гілкою з
індуктивністю .
Відтак:
.
Відтак:

 і
і




Рисунок 12.10
Припускаючи
у колі нульові початкові умови
 ,
для моменту
,
для моменту одержимо:
одержимо:


 ,
звідки
,
звідки

 .
.
Остаточно одержимо:


 ,
(12.33)
,
(12.33)
а
напруга на індуктивності і струми
 і
і дорівнюють:
дорівнюють:




 ;
(12.34)
;
(12.34)


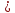

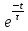 ;
(12.35)
;
(12.35)




 (12.36)
(12.36)
Часові діаграми струмів у колі показані на рис.12.11.

Рисунок 12.11
