3.3 Построение фигуры сечения

Задача на построение линии пересечения поверхности многогранника с плоскостью является позиционной. И решить ее можно двумя способами. Первый способ состоит в многократном решении основной позиционной задачи на пересечение прямой с плоскостью. Достаточно найти точки пересечения ребер призмы с плоскостью треугольника, или, наоборот, точки пересечения сторон треугольника с гранями (плоскостями) призмы. Последовательно соединяя полученные точки отрезками прямых, получим линию пересечения призмы с треугольником.

Второй способ состоит в последовательном, многократном решении задачи на построение линии пересечения двух плоскостей, а именно, плоскости треугольника с плоскостью одной из граней призмы, затем плоскости того же треугольника с плоскостью другой грани призмы, и т.д.

Рассмотрим решение задачи для обоих вариантов задания.

3.3.1.Пересечение призмы с треугольником

Рассмотрим решение задачи способом последовательного пересечения прямой с плоскостью (рис. 6), принимая грани призмы за плоскости общего положения, а стороны треугольника – за прямые общего положения.

Решение начинается на фронтальной плоскости проекций. Через сторону треугольника АС проведем вспомогательную фронтально - проецирующую секущую плоскость . Так как эта плоскость  перпендикулярна к фронтальной плоскости проекций, то ее проекцией на плоскость ₂ будет прямая ₁, совпадающая с фронтальной проекцией стороны треугольника АС. Точки пересечения ₁ с ребрами FF₁, DD₁ и EE₁ обозначим соответственно 1, 2 и 3. Проведем из этих точек линии связи до пересечения с соответствующими ребрами на горизонтальной плоскости проекций (направление указано стрелками) и получим точки 1, 2 и 3. Соединив эти точки тонкой прямой линией, получим фигуру – треугольник 1-2-3. Эта фигура есть результат пересечения призмы фронтально - проецирующей плоскостью ₁. Отметим одну особенность. На плоскости ₂ мы не видим этот треугольник, т.к. его плоскость лежит в плоскости ₁, а она проецируется в линию; на горизонтальной плоскости проекций мы видим, что проекция этого треугольника пересекается со стороной АС в двух точках М и К. Это и есть пересечение прямой АС с гранями призмы. Проведем линии связи из этих точек М и К на плоскость ₂ и отметим на стороне АС фронтальные проекции М и К (стрелки указывают направление на ₂).

Смысл таких построений следующий: точка М лежит на линии 3 - 2, принадлежащей грани DD₁E₁E, следовательно, М является точкой пересечения прямой АС с этой гранью, соответственно точка К – результат пересечения этой же прямой с другой гранью E₁EFF₁. Иными словами, прямая АС пронизывает призму в точке М и выходит в точке К. Считая призму непрозрачной линию М - К необходимо изобразить как невидимую (штриховой линией).

Аналогично проводим вспомогательную секущую плоскость ₂ через ребро призмы DD₁ (₂ перпендикулярна ₂). Эта плоскость пересекает треугольник АВС по прямой, проходящей через точки 4 и 5. Точка 4 лежит на стороне АВ (ее построение изложено ниже), а точка 5 – на стороне АС. Проведя соответствующие линии связи до пересечения на горизонтальной плоскости с проекциями сторон призмы АВ и АС получаем горизонтальные проекции точек 4 и 5, через которые проводим прямую 4 – 5. На горизонтальной плоскости проекций эта прямая пересекается с ребром DD₁ в точке P. От этой точки проводим линию связи вверх до пересечения с ребром DD₁. Таким образом, ребро DD₁ пересекается с плоскостью треугольника АВС в точке P.

Рис. 6.

Объединив результаты геометрических построений в одно целое, видим, что точки P и М принадлежат плоскости треугольника АВС, следовательно, линия P – М есть прямая, по которой пересекается грань DD₁E₁E с треугольником АВС. Аналогично, линия P – К является прямой, по которой треугольник АВС пересекается с гранью ЕЕ₁F₁F. Таким образом, треугольник P-M-K является результатом пересечения призмы с плоскостью.

Все эти геометрические построения можно было выполнить, начиная с горизонтальной плоскости проекций, проведя горизонтально - проецирующие вспомогательные секущие плоскости.

В некоторых вариантах задач сторона треугольника или ребро многогранника могут оказаться прямой частного положения.

В рассмотренном примере (см. рис. 6) такой прямой является сторона треугольника АВ (профильная прямая уровня). На фронтальной плоскости проекций ₂ пересекает АВ в точке 4. Чтобы построить эту точку на горизонтальной плоскости проекций, используем теорему Фаллеса (отношение отрезков прямой линии равно отношению их проекций) (рис.7):

Р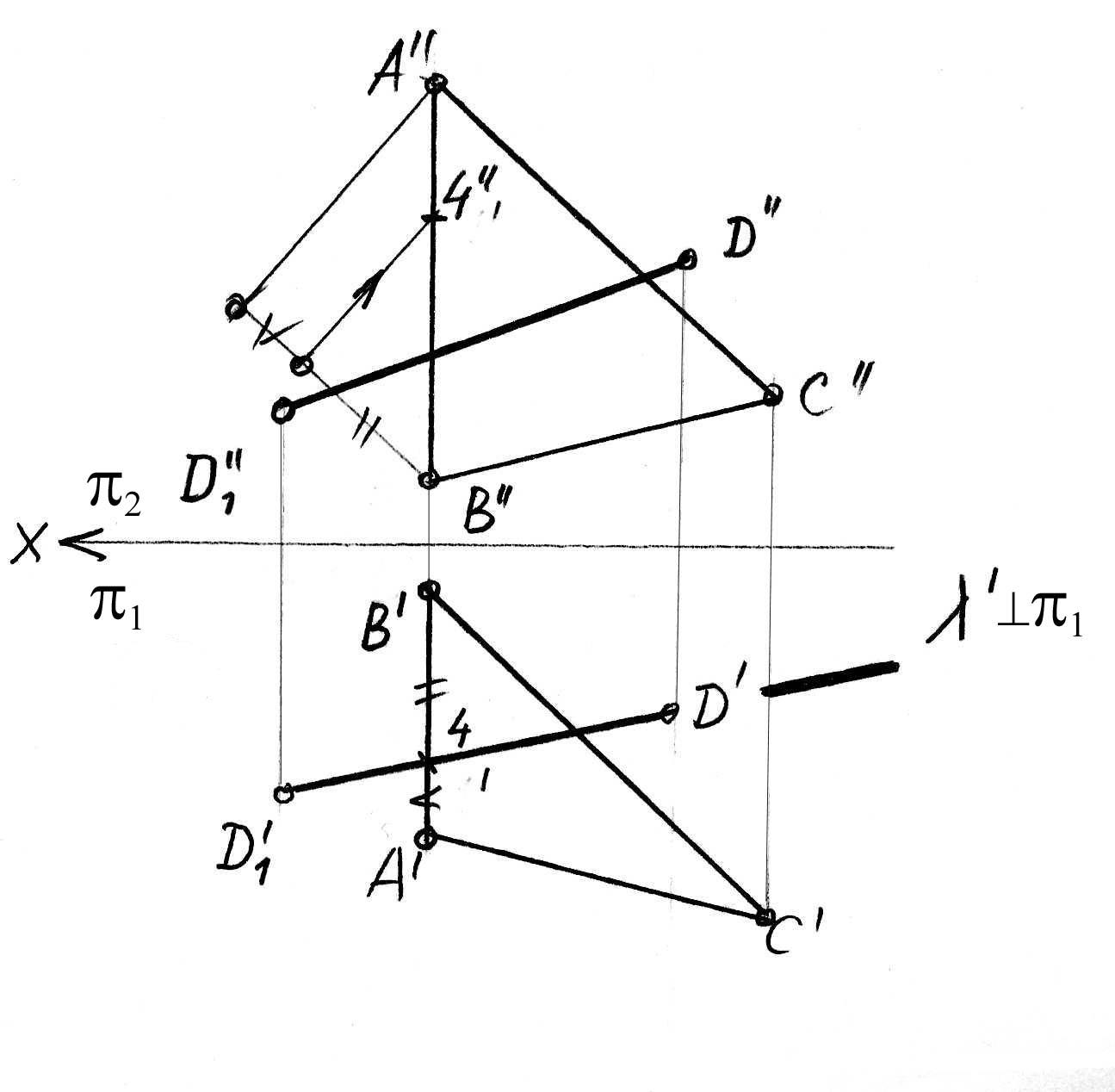ис. 7. Рис. 8.

Для этого на плоскости π₁ (см. рис.6) в удобном месте чертежа строим треугольник АВВ₀, помня о том, что точка 4 лежит ближе к точке В, чем к точке А. В этом треугольнике сторона АВ₀ равна стороне АВ, и отрезок А - 4₀ равен отрезку А - 4. Проводим линию В₀ - В и параллельно ей по стрелке линию 4₀ - 4. На пересечении АВ с этой линией будет лежать точка 4, и она разделит сторону АВ в том же отношении, что и точка 4 на фронтальной плоскости проекций разделит сторону АВ.

Аналогично можно построить точку 4 на π₂, если секущая плоскость будет проведена через ребро DD₁ на горизонтальной плоскости проекций (рис 8).