Пример №11

Для статически неопределимой рамы (рис. 68, а) требуется:

1. построить эпюры внутренних усилий, используя метод сил;

2) выполнить деформационную проверку, приняв

Решение

Определим степень статической неопределимости. Рама имеет пять связей, в то время как три связи равновесие плоской системы обеспечивают три связи. Значит, рама дважды статически неопределима.

Образуем основную систему (рис. 68, б), которая является статически определимой и геометрически неизменяемой. Приложив к ней внешнюю нагрузку и неизвестные усилия в лишних связях Х₁, Х₂ получим эквивалентную систему (рис. 68, в).

Запишем канонические уравнения метода сил для дважды статически неопределимой системы:

Построим эпюру изгибающих моментов в основной системе от внешних сил.

Участок 1

Участок 2

Участок 3

Рис. 68. Статически неопределимая рама: а – расчетная схема,

б – основная система, в – эквивалентная система

Рис. 69. Эпюра от внешних сил в основной системе

Построим эпюры изгибающих моментов 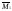и 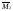от единичных сил по направлению усилий,.

Рис. 70. Эпюра от силы X1=1 (б) в основной ситеме (а)

Участок 1

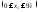
Участок 2

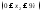
На участке 3

Рис. 71. Эпюра от силы X2=1 (б) в основной ситеме (а)

Участок 1

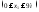
Участок 2

Участок 3

Запишем каноническое уравнение метода сил для системы дважды статические неопределимой.

Определим коэффициенты канонических уравнений по правилу Верещагина:

;

;

;

;

.

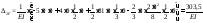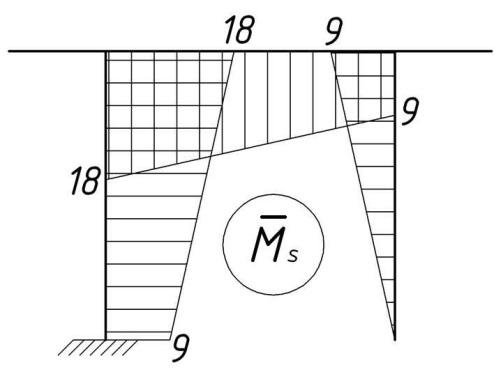
Рис. 72. Суммарная единичная эпюра

Для проверки единичных коэффициентов построим суммарную единичную эпюру путем сложения ординат эпюри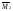 и «перемножим» ее саму на себя:

.

Полученный результат должен быть равен сумме «единичных» коэффициентов

.

;

.

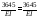Для проверки «грузовых» коэффициентов «перемножим» грузовую эпюру M_F и суммарную единичную эпюру :

.

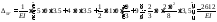Полученный результат должен быть равен сумме грузовых коэффициентов:

.

Имеем

.

Совпадение результатов говорит о правильности вычисления коэффициентов.

Подставим их значения в канонические уравнения и сократим на общий множитель:

_{Решив систему уравнений получим:}

X₁=–3,98кН; X₂=2,14кН.

Знак «минус», свидетельствуют о том, что принятое направление Х₁ следует изменить на противоположное.

Строим эпюры внутренних усилий N, Q, M с учетом найденных значений Х₁ и Х₂, используя метод сечений.

Рис. 73. Эквивалентная система

Участок 1

Участок 2

Участок 3

Участок 4

Участок 5

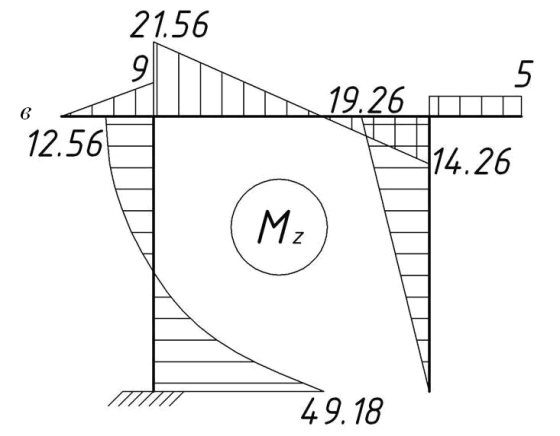
Рис. 74. Эпюры внутренних усилий в раме: а – продольной силы;

б – поперечной силы; в – изгибающего момента

Произведем деформационную проверку. «Перемножим» эпюры M_z и . При этом результат должен быть близок к нулю (погрешность не должна превышать 5%).

погрешность

Задача № 12

Для стойки указанного сечения, одинаково закрепленной в плоскостях xy и xz и сжатой центрально приложенной силой F, требуется подобрать размеры поперечного сечения, c учетом коэффициента продольного изгиба. Материал – сталь Ст.3.

Исходные данные: F =300 кН; l =2 м; R= 220 МПа.

Рис. 75. Центрально сжатый стержень: а– расчетная схема;

б– поперечное сечение

Решение

Для стойки, имеющей защемляющую и шарнирную опоры, коэффициент приведенной длины μ = 0,7. Определим геометрические характеристики сечения:

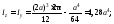
_{радиусы инерции сечения}

Гибкость стержня

.

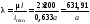Коэффициент продольного изгиба может принимать значения от нуля, до единицы. В первом приближении принимаем тогда:

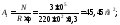
По табл. (приложения 6) принимаем значение , которое существенно отличается от φ_1.

_{Во втором приближении коэффициент продольного изгиба приним}аем как среднее арифметическое:

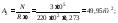
По табл. (приложения 6) принимаем значение , которое отличается от_.

_{В третьем приближении коэффициент продольного изгиба приним}аем как среднее арифметическое:

По табл. (приложения 6) принимаем значение

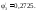
Вычислим напряжения в третьем приближении:

_{Перенапряжение составляет}

_{Что в пределах допустимых 3%.}

_{Окончательно принимаем a=4 см.}