Пример №9

Короткий чугунный стержень с тавровым поперечным сечением сжимается продольной силой F= 200 кН, приложенной в точке А (рис. 63). Требуется:

1) проверить условие прочности стержня, если допускаемые напряжения при сжатии а при растяжении

2) определить положение нейтральной оси и построить эпюру σ, приняв за базу перпендикуляр к нейтральной оси.

Решение:

Поскольку формула для определения напряжений при внецентренном растяжении-сжатии ориентирована на характеристикиглавные центральные оси инерции, то их определение составляет первоочередную необходимость.

Сечение имеет вертикальную ось симметрии у_с, которая и является одной из главных центральных осей инерции.

Рис. 63. Сечение внецентренно сжатого стержня и эпюра

нормальных напряжений

Представим сплошное сечение вертикальным прямоугольником площадью и горизонтальным, площадью . Координата центра тяжести сложного сечения:

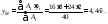
Моменты инерции относительно главных центральных осей:

где – расстояния центров тяжести прямоугольников до осиz_o.

Изгибающие моменты, входящие в формулу для определения напряжения, создаются сжимающей силой F = –200 кН, которая приложена в точке А с координатами т. А(3; –0,4). Они равны:

Наибольшие значения напряжений в растянутой и сжатой зонах можно вычислить, если известны координаты «опасных» точек. Эти точки наиболее удалены от нейтральной оси, положение которой определяется отрезками у_о, z_o, отсекаемыми ею на осях координат. При этом:

, .

Квадраты радиусов инерции равны:

, .

Таким образом,

, .

Проведя нейтральную ось, находим наиболее удаленные от нее точки В(–3; –0,4) и D(3; –4,4).

Определим напряжения в этих точках:

На перпендикулярах к базовой линии отложим в масштабе значения напряжений для точек В и D и, соединив эти точки прямой линией, построим эпюру σ. Используя эту эпюру легко определить напряжения в любой точке сечения. Для этого достаточно восстановить перпендикуляр к базовой линии из этой точки, измерить отрезок и, зная масштаб построения эпюры, определить величину напряжения в точке.

Условие безопасной прочности в сжатой зоне выполняется, так как<МПа. Условие прочности в растянутой зоне , тоже выполняется, так как 28,15МПа< 30 МПа.

Пример №10

Для статически неопределимой балки (рис. 64, а) требуется:

1) построить эпюры и, используя метод сил;

2) проверить условие прочности балки заданного сечения, приняв

Решение

Определим степень статической неопределимости балки. На балку наложены четыре связи, в то время как равновесие плоской системы обеспечивают три связи, и следовательно система один раз статически не определима.

Образуем основную систему отбрасыванием лишней связи и внешних усилий (рис. 64, б) и эквивалентную систему, систему с заданной нагрузкой и неизвестнойХ₁ лишней связи (рис. 64,в).

Построим эпюру изгибающих моментов M_Fот сил, приложенных к основной системе.

Рис. 64. Статически неопределимая балка: а – расчетная схема,

б – основная система, в – эквивалентная система

Рис. 65. Эпюра от внешних сил (б) в основной система (а)

Участок 1

Участок 2

Участок 3

Участок 4

Эпюра M_F представлена на рис. 65.

Строим эпюру изгибающих моментов от единичной силы Х₁=1.

Рис. 66. Эпюра от единичной силы (б) в основной системе (а)

Участок 1

Запишем каноническое уравнение метода сил для однажды статически неопределимой системы:

.

Определяем ипо правилу Верещагина:

;

Решая уравнение

,

получаем

.

Строим эпюры Q и M с учетом найденного значения Х₁.

Рис. 67. Эквивалентная система: а – расчетная схема;

б – эпюра поперечных сил; в – эпюра изгибающих моментов

Участок 1

Участок 2

Участок 3

Участок 4

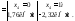
Произведем деформационную проверку.

«Перемножим» полученную эпюру M_z и единичную эпюру по правилу Верещагина. При этом результат должен быть близок нулю (погрешность не должна превышать 5%).

;

погрешность

Проверим условие прочности балки заданного сечения по нормальным напряжениям. Опасным является сечение, в котором возникает максимальный по абсолютной величине изгибающий _{момент Mmax=8кН·м. Из сортамента выписываем для швеллера №20 величину Wz=143см3. Получаем}

что меньше