2.1.1 Погрешности бинс.

Необходимо проанализировать погрешности, возникающие в процессе эксплуатации БИНС.

Режим (алгоритм) работа ИНС, когда её элементы и устройства идеальны (не имеют инструментальных погрешностей) и начальные условия функционирования системы точно соответствуют начальным обстоятельствам движения объекта, называют режимом (алгоритмом) идеальной работы. В реальных условиях инерциальным чувствительным элементам присущи различного рода погрешности.

Режим работы ИНС, при котором её элементы функционируют с погрешностями и начальные условия не соответствуют начальным обстоятельствам движения объекта называют возмущением.

Уравнения для отклонения переменных, характеризующих состояния БИНС, от их значений при идеальной работе, называют уравнением погрешностей[31]. Анализируя погрешности, можно в определенной степени упростить алгоритмы, по которым работает вычислительное устройство, а также выработать обоснованные требования к коррекции БИНС.

Ошибки БИНС в случае неточного определения вертикали.

Рассмотрим случай, когда акселерометры и гироскоп функционируют без ошибок, а вертикаль в начальный момент задана с ошибкой. В этом случае безошибочные показания акселерометров определяются равенствами[30](предполагается, что :

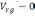
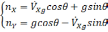
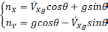(2.1)

где nx, ny – величина кажущегося ускорения относительно осей х и y, VXg - скорость, θ - угол.

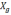
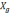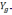
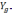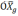
Для определения местоположения БЛА (широты φ) необходимо перепроектировать показания акселерометров (2.1) в географическую систему координат, т.е. на оси О и О Однако за счёт неточного задания вертикали сигналы акселерометров (2.1) будут пересчитываться не на оси географического трехгранника, а на ос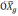и и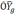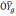вычисленной системы координат. В этом случае получим:

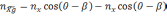
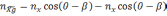(2.2)

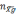
где - проекция кажущегося ускорения на географическую систему координат, β - угол

Для малого угла β, подставив (2.2) в (2.1), получим проекцию кажущегося ускорения:

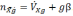
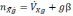(2.3)

Таким образом, после пересчёта данных в географическую систему координат в проекции кажущегося ускорения 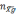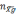содержится составляющая вектора ускорения силы тяжести.

Согласно дальнейшим расчетам [31]

β(t)=(2.4)

где

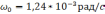
Эту частоту можно трактовать, как частоту малых незатухающих колебаний в поле силы тяжести Земли физического маятника, приведенная длина которого равна расстоянию от центра Земли до объекта, движущегостя на высоте h. Числовое значение частоты Шулера равно 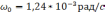, соответственно период Шулера Т=84,4[*].

Из решения следует, что вычисленная вертикаль будет совершать колебания относительно истинной вертикали с периодом Шулера.

Согласно расчётам [31], ошибка определения скорости связана с ошибкой построения вертикали.

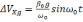
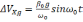(2.5)

Ошибка определения широты:

Δφ=(2.6)

Ошибка определения пройденного расстояния ΔS:

ΔS=R (2.7)

На рисунке 2.1 показаны ошибки БИНС, вызванные неточным заданием вертикали, таким образом, отклонение аналитической вертикали от истинной, ошибки в определении скорости и местонахождения БЛА имеют колебательный характер, период их колебания равен периоду Шулера.

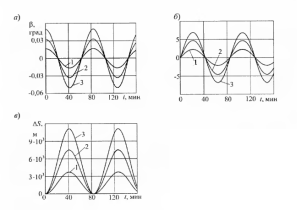
Рисунок 2.1 Ошибки БИНС, вызванные неточным задание вертикали: а) ошибка построения вертикали б) ошибка определения скорости, в) ошибка в определении пройденного расстояния; 1 - 2 -3 -.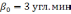

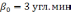Ошибки БИНС, вызванные погрешностью акселерометров.

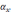
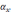Пусть в БИНС начальные условия выдержаны точно, а в показаниях акселерометров имеются погрешности (смещение нуля) δи δ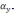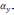В этом случае уравнения(2.1) примут вид:

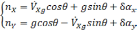
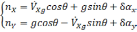(2.8)

проекцию кажущегося ускорения:

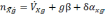
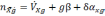(2.9)

где sinθ – проекция ошибок акселерометров на ребро О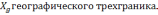

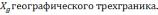
β(t)=

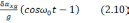
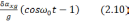
Из решения следует, что погрешности акселерометра вызывают колебания вертикали с периодом Шулера относительно смещенного от истинной вертикали положения равновесия на величену β(t)= колебаний равна ошибке акселерометра в доле ускорения силы тяжести.

Ошибка определения скорости.

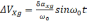
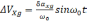(2.11)

Ошибка определения широты и пройденного расстояния:

Δφ=(2.12)

ΔS=(2.13)

На рисунке 2.2 показаны ошибки вызванные погрешностью акселерометров.

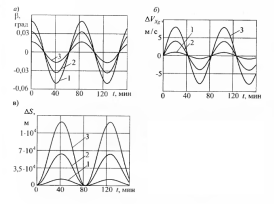
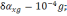
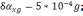
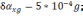Рисунок 2.2 Ошибки БИНС, вызванные погрешностью акселерометра: а) ошибка построения вертикали б) ошибка определения скорости, в) ошибка в определении пройденного расстояния; 1 - 2 -3 -.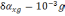

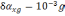Ошибки БИНС, вызванные дрейфом гироскопов

Пусть теперь начальные данные выдержаны точно, акселерометр функционирует идеально, а датчик угловой скорости измеряет абсолютную угловую скорость БЛА с ошибкой ε. Найдем ошибку в определении тангажа. Тангаж определяется[30], как результат интегрирования относительно угловой скорости связанного трехгранника

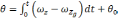
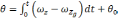(2.14)

где – ωx, ωz-; ε-собственный дрейф гироскопа

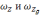
Наличие собственного дрейфа гироскопа ε приведет к погрешности в определении проекции 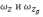абсолютной угловой скорости связанного и географического трехгранников, соответственно. Расчетное значение угла тангажа можно представить в виде:

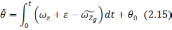
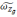
где 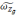- рассчитанная с помощью БИНС проекция угловой скорости географического трехгранника.

После некоторых преобразований [31] получаем связь между истсинным и вычисленным значением тангажа

θ-=β или Δθ=β (2.16)

Таким образом, при одноканальном анализе БИНС ошибка выработки тангажа равно ошибке построения вертикали с обратным знаком.

Ошибки определение вертикали, скорости, широты и пройденного пути:

β(t)= -

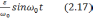
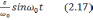
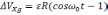
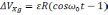(2.18)

Δφ=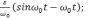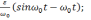(2.19)

ΔS=(2.20)

где-

Из формул видно, что вычисленная вертикаль по –прежнему совершает колебания истинной вертикали с частотой Шулера и амплитудой . В ошибке определения скорости имеется постоянная составляющая, пропорциональная радиусу Земли. Нарастание со временем погрешности БИНС является главным их недостатком.

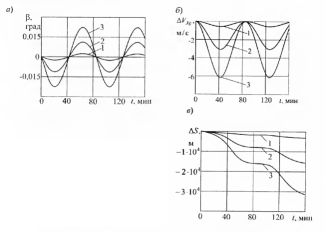
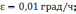
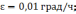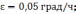
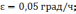Рисунок 2.3 Ошибки БИНС, вызванные дрейфом гироскопа: а) ошибка построения вертикали б) ошибка определения скорости, в) ошибка в определении пройденного расстояния; 1 – 2 -3 -.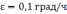

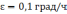Ошибки вертикального канала БИНС.

Рассмотрим погрешности вертикального канала, вызванные ошибкой компенсации ускорения силы тяжести g

Положим, гироскоп и акселерометры работают без ошибок, а начальные данные введены точно. В соответствии с принципом работы вертикального канала найдем ошибку в определении вертикальной скорости БЛА, как разность между вычисленной и истинной вертикальной скоростью

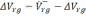
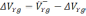(2.21)

Из [31] находим:

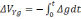(2.22)

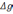
где 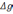- ошибка компенсации ускорения силы тяжести

Очевидно, что ошибка в определении высоты выглядит так

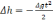
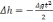(2.23)

Из формул можно заключить, что ошибки в определении вертикальной скорости и высоты с помощью БИНС растут неограниченно. Беспредельный рост ошибок вертикального канала БИНС называется неустойчивостью этого канала.

Ошибки определение вертикали, скорости, широты и пройденного пути:

β(t)=- -

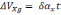
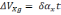(2.25)

ΔS=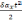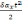(2.26)

Из соотношений видно, что при отсутствии вектора ускорения силы тяжести ошибка построения вертикали, а также ошибки в определении скорости и координаты, вызванные смещением нуля акселерометра, неограниченно возрастает.