Интегральная оценка качества

Интегральная оценка качества относится к аналитическим методам исследования САУ и дает общую оценку скорости затухания и отклонения управляемой величины в совокупности, без определения указанных пара­метров в отдельности.

Простейшей интегральной квадратичной оценкой является оценка вида



J₀ =  e²(t)dt,

⁰

где e(t) = g(t) - y(t)- ошибка системы;g(t)- задающее воздейс­твие;y(t)- регулируемая величина.

Если e(t) имеет постоянную составляющую в виде установившегося значения e_уст, то интеграл J₀ будет расходящимся, поэтому в качестве ошибки берут динамическую ошибку системы е₁, т.е. отклонение регулиру­емой величины y(t) от ее установившегося значения

e₁(t) = y_уст - y(t) = g(t) - e_уст - y(t) = e(t) - e_уст.

Интегральная квадратичная оценка может быть определена по изобра­жению ошибки

 c+j

Jо =  e₁²dt = [ E₁(p)E₁(-p)dp] / 6,28j. (5)

- c-j

Для практических целей более удобной является формула Релея, ко­торая получается из (5) заменой p=j

 

J₀= [ |E₁(j)|² d] / 2j = [ |W_e(j)|²|G(j)|² d] / 2j. (6)

-  - 

Если подынтегральное выражение представить в виде

|E1(j)|² = |We(j)|²|G(j)|² = B(j) / |A(j)|² = B(j) / [A(j)A(-j)],

где A(j) = a₀(j)ⁿ+a₁(j)^n-1+...+a_n-1()+a_n; (7)

B(j) = b₀(j)^2n-2+b₁(j)^2n-4+...+b_n-2(j)²+b_n-1, (8)

то интеграл (6) вычисляется по формуле



J₀ = [[B(j) / |A(j)|]d] / 2 = (-1)M_n / [2a₀D_n], (9)

- 

где | a₁ a₃ a₅ a₇ ... 0 |

| a₀ a₂ a₄ a₆ ... 0 |

D_n = | 0 a₁ a₃ a₅ ... 0 | - старший определитель Гурвица

|.................……|

| 0 0 0 0 ... a_n|

| b₀ b₁ b₂ ... b_n-1|

M_n = | a₀ a₂ a₄ .… 0 |

|.................……|

| 0 0 0 .… a_n |

Выбор оптимальных параметров управляющего устройства по минимуму интегральной оценки

При заданной структуре САУ задача выбора параметров сводится к следующему. Необходимо отыскать такие значения изменяемых параметров управляющего устройства, при которых интегральная квадратичная оценка принимает минимальное значение, значения изменяемых параметров, дос­тавляющих минимум интегральной квадратичной оценке, могут быть найдены путем взятия частных производных по названным параметрам.

В исследуемой в данной лабораторной работе САУ изменяемым пара­метром управляющего устройства является постоянная времени интегриро­вания Т_и. Все остальные параметры объекта и управляющего устройства заданы постоянными. Следовательно, задача состоит в определении опти­мального Т_иопт, при котором J₀ = min. Применительно к системам с И- и ПИ-регуляторами и объектом управления, у которого Т₁ = Т₂, динамичес­кая ошибка может быть представлена следующим образом:

И-регулятор:

E₁(p) = [1 / p][1 + W₀(p)W_p(p)] =

= [T_иT₁²p² + 2T_иT₁p + T_и] / [T_иT₁₂p³ + 2T_иT₁p² +T_иp + K₀];

ПИ-регулятор:

E₁(p) = [1 / p][1 + W₀(p)W_p(p)] =

= [T_иT₁²p² + 2T_иT₁p + T_и] / [T_иT₁²p³ + 2T_иT₁p² + T_и(1 + K_п K₀)p + K₀].

В соответствии с уравнениями (7) и (8) в данной работе полиномы A(j) и B(j) приобретают вид:

A(j) = T_иT₁²(j)³ + 2T_иT₁(j)² + T_и(1+K_п K₀)(j) + K₀; (10)

B(j) = T_и²T₁⁴(j)⁴ - 2T_и²T₁²(j)₂ + T_и². (11)

Коэффициенты a_i и b_i определителей M_n и D_n находятся из выражений (10) и (11):

a₀ = T_иT₁²; b₀ = T_и²*T₁⁴;

a₁ = 2T_иT₁; b₁ = -2T_и²*T₁²;

a₂ = T_и(1 + K_пK₀); a₃ = K₀; b₂ = T_и².

При подстановке этих коэффициентов в (9) для системы с ПИ-регуля­тором выражение интегральной квадратичной ошибки принимает вид:

J₀ = {Т_и[2Т_и + (3 + К_пК₀)K₀T₁]} / {2К₀[2Т_и(1 + К_пК₀) – К₀Т₁]}. (12)

Выражение J₀ для системы с И-регулятором получается из (12), как частный случай подстановкой К_п = 0

Jo = [Т_и(2Т_и + 3К₀Т₁)] / [2K₀(2Т_и – К₀T₁)]. (13)

Искомое значение Т_иопт, которое доставляет минимум квадратичной оценке, находят дифференцированием (12) и (13) поТ_ии приравниванием производных к нулю. Тогда получается:

- для ПИ-регулятора

Т_и = [(3 + К_пК₀)К₀Т₁] / [2(1 + К_пК₀)]; (14)

- для И-регулятора

Т_и = 4,55Т₁К₀. (15)

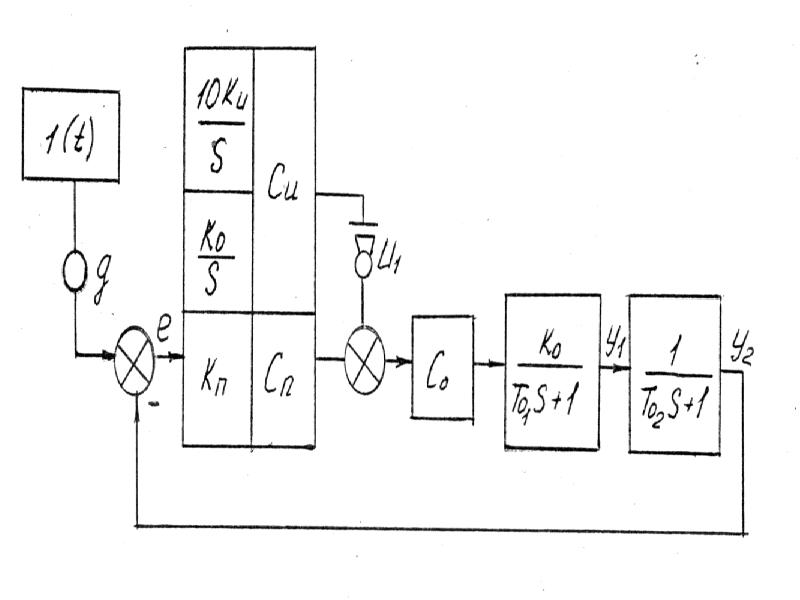Рис. 2.3. Схема моделирования исследуемой САУ на АВМ «СУЛ-3».

При схемотехнической и программной реализации рассмотренных регу­ляторов удобнее пользоваться коэффициентом передачи интегратора К_ие, который является обратной величиной по отношению к постоянной времени Т_и. В моделирующем блоке СУЛ-3 (рис.2.3) коэффициент К_ие определяется двумя па­раметрами К_и и С_и

К_ие = К_иС_и = (Т_и)^-1.

Исходя из выражений (14) и (15) и с учетом принятых на СУЛ-3 обозначений, можно записать следующие выражения для вычисления опти­мальных значений коэффициента передачи интегрирующего блока:

для ПИ-регулятора К_ие = [2(1 + К_пеК_0е)] / [К_пеТ₀₁(3 + К_пеК_0е)];

для И-регулятора К_ие = 0,22 / [К_0еТ₀₁],

где К_пе = - коэффициент передачи пропорционального блока;

К_ое = К₀С₀ - коэффициент передачи блока объекта управления;

Т₀₁ - постоянная времени блока объекта управления.