
- •Оглавление
- •Лекции 1,2. Введение
- •Лекции 3,4 применение автоматизированных навигационных комплексов
- •Основы автоматизированного решения навигационных задач современные проблемы воздушной навигации
- •Принцип и основные операции автоматизированного навигационного процесса
- •Общая схема работы анк
- •Основная система координат анк
- •Аналитические зависимости для решения задач в анк
- •Лекция 5. Способы оптимизации навигационной информации
- •Устройства управления, индикации и сигнализации
- •Характеристика типового автоматизированного навигационного комплекса с аналоговым вычислителем
- •Состав комплекса
- •Лекции 6, 7, 8 Автоматическая бортовая система управления абсу-134а
- •Комплекс автоматов ка-142
- •Командная пилотажно-навигационная система путь-4
- •Счисление и преобразование координат
- •Оптимизация (коррекция) счисленных координат
- •Лекции 9,10,11,12,13. Режимы управления самолетом
- •Решение задачи захода на посадку
- •Применение автоматизированных навигационных комплексов с цифровыми вычислителями
- •Характеристика автоматизированного навигационного комплекса с цифровым вычислителем
- •Общие принципы построения комплексных навигационных систем
- •Типы комплексных и комбинированных навигационных систем
- •Комплексная система, сочетающая анк с неавтономными радионавигационными устройствами
- •Комбинированная система инерциальной навигации в сочетании с доплеровским измерителем w и ус
- •Комбинированная система навигации (анк в сочетании с доплеровским измерителем w и ус)
- •Комплексная система навигации (анк в сочетании с панорамным радиолокатором и астрокорректором курса)
- •Комплексные системы, сочетающие инерциальные средства с астрономическими и радиолокационными корректорами места
- •Лекция 14 комплексные системы навигации, определяющие место самолета в единой системе координат
- •Лекция 15 базовый навигационный комплекс "ольха-1"
- •Базовый пилотажный комплекс бпк-1п-42
- •Датчик усилий дублированный дду-4 сер. 03
- •Информационный комплекс высотно-скоростных параметров ик всп-1-6
- •Блок формирования и контроля бфк-3
- •Система сигнализации комплексов бпк-1п-42, "Ольха-1" и ик всп-1-6
- •Сигнализация режимов работы и отказов пилотажного комплекса. Формирование информации
- •Лекция 16 комбинированный прибор да-30п
- •Базовая система формирования курса бсфк-1 с гироагрегатами га-8 и блоками усилителей бу‑12 сер. 2
- •Лекция 17 цифровая вычислительная маШиНа цвм20-1м
- •Пульт ввода и индикации пви-1пм
- •Лекция 18 пульт подготовки и контроля ппк
- •Пульт управления пу-1п
- •Блок коммутации бк-1п
- •Преобразователь кода дальности пкд
- •Картографический планшет пк-4-42
- •Лекция 19 бортовой навигационный комплекс «пижма‑1»
- •Состав и функциональное построение комплекса
- •Навигационный комплекс для средних магистральных самолетов Ту-154м ("Жасмин")
- •Цифровая вычислительная машина цвм 80
- •Лекция 20 комплекс стандартного пилотажно-навигационного оборудования кспно-204
- •Вычислительные системы самолетовождения, управления полетом и тягой
- •Вычислительная система самолетовождения всс-85
- •Вычислительная система управления полетом всуп-85
- •Вычислительная система управления тягой всут-85
- •Лекция 21 Системы предупреждения критических ситуаций
- •Система предупреждения критических режимов полета спкр-85
- •Система предупреждения приближения земли сппз-85
- •Система воздушных сигналов свс-85
- •Обзорные радиолокационные системы
- •Метеонавигационная радиолокационная станция мнрлс-85-204
- •Бесплатформенная инерциальная навигационная система и42-1с
- •Бесплатформенная инерциальная навигационная система irs hg1150фирмыhoneywell
- •Лекция 22 Бортовая аппаратура радиотехнических и посадочных систем
- •Радиотехническая система ближней навигации а-331
- •Радиотехническая система дальней навигации рсдн-85
- •Спутниковая навигационная система снс-85
- •Система посадки по радиомаякам типа ilSи сп- 50 -ils-85
- •Микроволновая система посадки mls-85
- •Радиотехническая система ближней навигации по маякам vor vor-85
- •Радиодальномер дме/р-85
- •Лекция 23 Автоматический радиокомпас арк-25
- •Радиовысотомер малых высот рв-85
- •Средства отображения индикации, сигнализации и системы контроля
- •Система электронной индикации сэи-85
- •Резервные приборы
- •Авиагоризонт агб-96р
- •Радиомагнитный индикатор рми-3
- •Магнитный жидкостной компас ки-13бс
- •Система сбора и локализации отказов ссло-85
- •Антенна акн-005-204
- •Хронометр авиационный электронный хаэ-85м
- •Антенно-фидерное устройство рсбн "Астра-204"
- •Комплексный пульт радиотехнических средств кп ртс
- •Лекция 24 Современные комплексы
- •Бортовой комплекс радиоэлектронного оборудования aria-200
- •Интегрированный комплекс навигации и посадки икнп
- •Электромагнитная система ориентации и навигации малого радиуса действия для точной посадки беспилотных летательных аппаратов
- •Комплекс цифровой пилотажно-навигационный цпнк-114
- •Лекция 25 Пилотажно-навигационный комплекс пнк-10
- •Интегрированная навигационная система
- •Комплексная вычислительная система самолетовождения квсс-140
Аналитические зависимости для решения задач в анк
Современная вычислительная техника, особенно цифровая, позволяет реализовать сложные математические зависимости сфероидической геометрии и решать по ним навигационные задачи с любой необходимой степенью точности. Однако невысокая точность исходных данных (особенно при использовании курсовых приборов) позволяет для решения задач воздушной навигации считать поверхность Земли сферической и применять математический аппарат сферической тригонометрии. Этому соответствует и применение в АНК ортодромической системы координат в качестве основной. В то же время все исходные координаты точек на земной поверхности известны только в географической системе, т. е. на эллипсоиде.
В зависимости от требуемой точности замена эллипсоида шаром выполняется различными методами.
В простейшем случае Земля принимается за шар с радиусом R= 6371 км, а геосферические координатыφиλсчитаются равными географическимφгеогриλгеогр; такое упрощение приводит к максимальным ошибкам в расстояниях до 0,5% и в углах — до 0,4°.
В другом случае исходные географические координаты φгеогр иλгеогрпредварительно с помощью метода проф. В. В. Каврайского переводятся в геосферические по формулам:
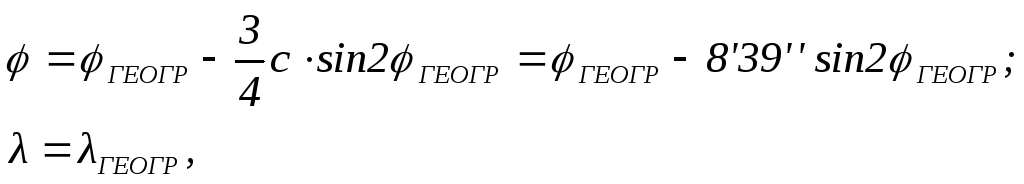
а Земля считается шаром с радиусом R=a(1-c/4)=6372,9км,
где а = 6378245м — большая полуось эллипсоида Красовского,
с=(a-b)/a 1/300 — его сжатие,
b = 6356863 м — малая полуось.
Этот прием обеспечивает уменьшение максимальных ошибок до 0,08% в расстояниях и до 6' — в углах.
Наконец, пересчет географических координат в геосферические можно выполнять по тем же формулам, но радиус Земли выбрать таким, чтобы вдоль заданной ортодромии частный масштаб отображения эллипсоида на сфере был равен единице:
![]()
где φиβ— геосферическая широта и путевой угол в любой, в том числе и начальной, точке заданной ортодромии (так как вдоль ортодромии произведениеsinβcosφ=const). При этом методе достигается точность отображения расстояний до 0,001%.
Однако и сферические зависимости используются часто только для подготовки исходных данных, вводимых в АНК, а само решение навигационных задач ведется по еще более простым зависимостям—формулам прямолинейной тригонометрии. Это обеспечивает значительное упрощение аппаратуры навигационных вычислителей, сохраняя в то же время при определенных условиях вполне удовлетворительную точность результатов.
Возможность применения плоской тригонометрии в навигационных задачах зависит от величин рассматриваемых расстояний, которые лишь в отдельных случаях достигают нескольких тысяч километров (при счислении координат над океаном между коррекциями и при использовании систем дальней радионавигации). При применении же БРЛС, большей части УНС и УДНС ближней навигации расстояния не превосходят 400—500 км.
Представление о степени искажения результатов расчетов при замене сферических треугольников плоскими дает теорема Лежандра, согласно которой углы плоского треугольника со сторонами, равными сторонам сферического, будут уменьшены на 1/3 сферического избытка («эксцесса») данного сферического треугольника:
![]()
где SΔ— площадь сферического или, приближенно, плоского треугольника,aR— радиус земного шара. Например, при рассмотрении правильного треугольника со сторонамиD— 500 км
![]()
а при сторонах D = 1000 км — ΔА = 12'.
В основе счисления координат по формулам прямолинейной тригонометрии лежит использование упрощенной ортодромической системы координат с таким выбором главной ортодромии (оси Оу), чтобы ЛЗП на всех этапах проходила с возможно меньшими отклонениями от нее. В этих условиях точные («сферические») формулы счисления ортодромических координат при использовании ортодромического датчика курса принимают вид:
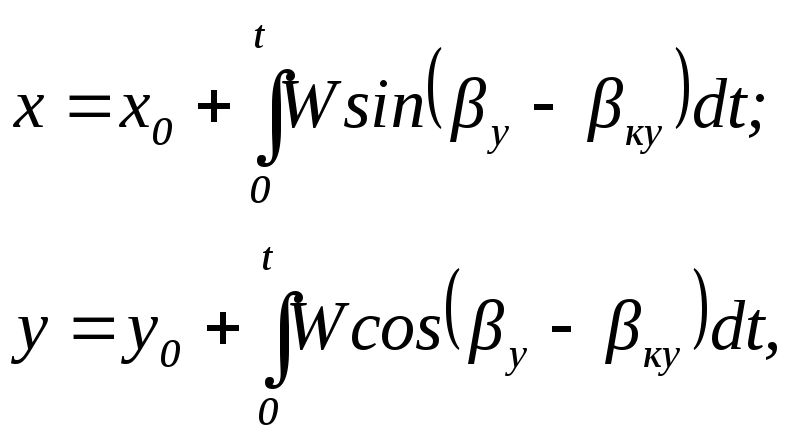
где βу— текущий условный путевой угол,βку— условный «угол карты» (заданный путевой угол главной ортодромии).
Применение в АНК упрощенных формул для счисления координат приводит к методическим ошибкам тем большим, чем больше фактические значения координаты хотличаются от нуля, т. е. при полете по маршрутам, не совпадающим с главной ортодромией. Нетрудно заметить, что при полете по ортодромическим меридианам, т. е. перпендикулярно главной ортодромии (βу — βку = 90°), методическая ошибка отсутствует (так какcos(βy — βку) = 0); наибольшей она будет при полетах с направлениями, близкими к главной ортодромии, но на некотором удалении от нее, когда уголβу — βкублизок к нулю. Известны расчеты, на основании которых можно показать, что неучет сферичности Земли в полете по ЛЗП, параллельной в начальной точке главной ортодромии, приводит к относительным радиальным ошибкам счисления МС, определяемым выражением
![]()
где S— пройденный путь,х0— начальное удаление от главной ортодромии, выраженное в радианах (долях радиуса Земли). Например, приS= 500 км = 0,079 рад и х0 = 200 км — 0,031 рад относительная ошибка МСr/S = 0,0013, а прих0= 100 км —r/S = 0,0006.
Однако в условиях полетов гражданской авиации для конкретного заданного маршрута всегда можно выбрать такое положение главной ортодромии, чтобы полет все время проходил вблизи нее, т. е. при малых значениях х, и тем самым практически исключить ошибки счисления, связанные с применением упрощенных формул. Даже в случаях возникновения в полете необходимости резко изменить маршрут в сторону от главной ортодромии современные АНК обеспечивают возможность оперативного перехода на счисление в системе координат, связанной с новой главной ортодромией, т. е. в области малых значений координатых.
Другая часть вычислительных операций, выполняемых АНК, представляет собой преобразования для перевода координат самолета, определенных различными независимыми методами, в координаты основной системы данного АНК, что необходимо для сравнения их со счисленными или с программными координатами.
В зависимости от применяемых средств (систем) независимого определения МС исходные координаты выражаются в разных системах: географической, биполярной (двуазимутальной), полярной сферической, гиперболической и др. При этом возможен как непосредственный переход от исходных координат к основным, так и через координаты промежуточной системы. Например, гиперболические координаты, определяющие положение МС относительно двух баз станций, могут быть предварительно пересчитаны в географические координаты или в сферические полярные относительно ведущей станции РДНС (ρ, θ), а затем уже в основную систему АНК — ортодромическую.
Применение упрощенных аналитических зависимостей (формул прямолинейной тригонометрии) при координатных преобразованиях допустимо, как правило, только при определении МС с помощью радионавигационных средств (систем) ближнего действия (БРЛС, УДНС ближней навигации), когда опорные ориентиры, используемые при определении МС, удалены от фактического места самолета и от ЛЗП не более чем на 300—350 км. В этих случаях сферические треугольники могут решаться как плоские с такими же сторонами и углами. Возможные при этом ошибки могут быть оценены с помощью теоремы Лежандра.
Вопросы студентам:
Каковы основные проблемы современной воздушной навигации. Как они решаются? Приведите примеры.
Как решаются задачи в АНК? В чем сущность метода непосредственной коррекции и метод управления навигационным режимом, чем они отличаются?
Чем обусловливаются навигационные возможности комплекса?
Что такое основная система координат АНК? Какие системы координат применяются в аппаратуре, входящей в АНК? Что такое ГО и ЧО?
Что такое сферическая система координат? Что делается для уменьшения ошибки представления геоида в виде сферы?
По каким формулам производится счисление ортодромических координат?
Как и для чего выбирается ГО? Для чего используется ЧО?
