1.9 Общая система уравнений качки корабля

Запишем уравнения Лагранжа движения твердого тела применительно к случаю качки:

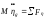;; _(1.106)

; ;_.

Суммы в правой части данных выражений представляют собой сумму действующих на судно сил:

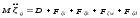_{; (1.107)}

_;

_;

_.

Здесь 1, 3 и 5 уравнения представляют собой уравнения продольной качки,а 2,4 и 6 уравнения поперечной качки. Подставляя в (1.107) полученные ранее выражения для гидростатических и инерционно-демпфирующих сил (1.51),(1.57),(1.61) и (1.74), получим :

(1.108)

Уравнения продольной качки

;

;

(1.109)

Продольная и поперечная качка судна, симметричного относительно ДП может рассматриваться раздельно. Если симметрия нарушена, вследствие начального крена или особенностей формы корпуса, то отдельные виды продольной и поперечной качки будут взаимосвязаны.

1.10 Вертикальная,бортовая, и килевая качки на спокойной воде

Рассмотрим поведение основных видов качки на спокойной воде. В условиях спокойной воды возмущающие силы отсутствуют, поэтому в правых частях уравнений (1.108-1.109 ) будет ноль.

Дополнительные виды качки: поперечно-горизонтальная, продольно-горизонтальная и рысканье сами по себе в условиях спокойной воды существовать не будут –данные виды качки будут апериодически затухать.

Рассмотрим уравнение изолированной вертикальной качки. В условиях спокойной воды оно будет иметь вид:

. (1.110)

Разделим все его составляющие на коэффициент при второй производной:

. (1.111)

где

.

Величина носит название собственной частоты вертикальной качки, т.е. той частоты, с которой судно совершает вертикальные колебания на тихой воде.

Решение однородного дифференциального уравнения (1.111) имеет вид:

_, (1.112)

-собственная частота с учетом сопротивления.

Для определения констант А_ζ и В_ζ используем следующие начальные условия . В момент времени t=0 ζ_g=ζ₀ и _g=0. Продифференцируем выражение (1.112):

(1.113)

Подставляя начальные условия в (1.112) и (1.113) получим:

_;

. (1.114)

Тогда

(1.115)

и в одночленном виде

, (1.116)

где

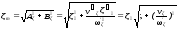-амплитуда,

- фаза вертикальных колебаний.

Период свободно затухающих вертикальных колебаний равен

, т.е. всегда несколько превышает собственный .

Амплитуда колебаний затухает по экспоненциальному закону тем интенсивней, чем больше относительный коэффициент демпфирования.

Рассмотрим подробнее процесс затухания амплитуд.

Перепишем в виде

(1.117)

Определим моменты времени, при которых отношение (1.117) приобретает экстремальные значения. Полагая =0, находим

…Отсюда t=0,

После подстановки в (1.116) будем иметь:

t=0 ;;

. (1.118)

Из (1.118) видно, что отношение двух последовательных амплитуд

. (1.119)

Логарифмируя, находим

. (1.120)

Величина , определяющая убывание натуральных логарифмов двух последовательных амплитуд, называетсялогарифмическим декрементом колебаний.

Используя формулу для периода

найдем

. (1.121)

Ясно, что чем больше отношение , тем быстрее убывает амплитуда вертикальной качки.

Уравнение килевой качки на спокойной воде имеет вид :

(1.122)

Здесь

Величина носит название собственной частоты килевой качки.

Структуры уравнений (1.122) и (1.111) одинаковы. Поэтому вывод его решения будет аналогичен выводу решения уравнения вертикальной качки.

Приведем его окончательный вид.

, (1.123)

где

,

.

Логарифмический декремент затухания килевой качки также аналогичен вертикальной :

, (1.124)

Остановимся более подробно на дифференциальном уравнении бортовой качки, которое на тихой воде имеет вид:

(1.125)

Поделив все члены на коэффициент при второй производной будем иметь

, (1.126)

где

Решение уравнения (1.126) имеет вид

(1.127)

А₀, В₀– постоянные интегрирования, определяемые из начальных условий; –собственная частота с учетом сопротивления.

Используем для определения А₀ и В₀ начальные условия, аналогичные соответствующим условиям для вертикальной качки. При t=0, θ=θ₀, _.

Дифференцируя зависимость (1.127) получим:

(1.128)

Подставляя начальные условия в (1.127) и (1.128) , найдем:

А₀=θ_0;

Подставляя найденные А₀ и В₀ в (1.127) получим:

(1.129)

Приведем выражение (1.129) к одночленному виду

, (1.130)

где

,

.

Подставим А₀ и В₀ в выражение (1.128). Получим:

(1.131)

Из выражения (1.131) следует, что угловая скорость бортовых колебаний будет равна нулю при

t=0,

Подставим данные значения времени в выражение для θ (1.130). Получим

t=0 ;

;

. (1.132)

Отсюда можно получить

(1.133)

Логарифмируем, находим

; (1.134)

.

Бортовая качка обладает самыми низкими значениями коэффициента демпфирования по сравнению с другими видами качки. Для нее справедливо считать, что _{. Тогда}

Отсюда

(1.135)

Отношение называется безразмерным коэффициентом демпфирования бортовой качки.

(1.136)

На формуле (1.136) основано экспериментальное определение коэффициента демпфирования бортовой качки.

Разница в характере затухающих вертикальных (килевых) и бортовых колебаний связана с различными величинами безразмерных коэффициентов затухания и.Опыты и расчеты показывают, что величины обычно в несколько раз больше..Поэтому вертикальная качка на спокойной воде затухает гораздо быстрее, чем бортовая. Так, запись свободно затухающей бортовой качки модели транспортного судна содержит обычно 10-12 полных колебаний (рис1.11), в то время как запись вертикальной- не более 4-5. Характерный вид записи свободно затухающей бортовой качки приведен на рис.1.11

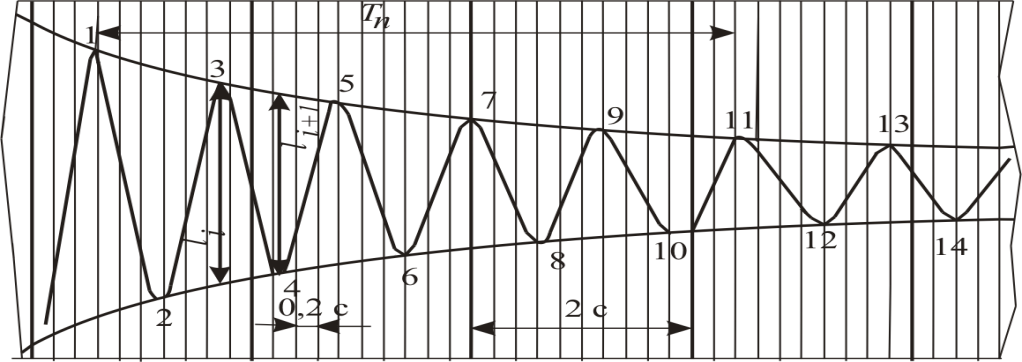
Рис. 1.11 Запись затухающих бортовых колебаний на тихой воде

11. Практическое определение собственных периодов качки.

Для того, что-бы определить собственные частоты и периоды вертикальной, килевой и бортовой качки необходимо предварительно вычислить значения моментов инерции массы корабля и присоединенных масс.

Общие выражения для моментов инерции массы корабля относительно центральных продольной и поперечной осей имеют вид ;

(1.137)

На практике данные интегралы вычисляются путем суммирования моментов инерции составляющих нагрузки относительно соответствующих осей. Для приближенного вычисления моментов инерции масс используются следующие формулы :

; (1.138)

(1.139)

где H-высота борта; α-коэффициент полноты площади ватерлинии;δ-коэффициент общей полноты.

Для определения суммарного значения может быть применена следующая эмпирическая формула :

(1.140)

где -приведенный радиус инерции корабля с учетом присоединенной массы воды

(1.141)

С- эмирический коэффициент [4]

(1.142)

Для приближенной оценки присоединенных масс можно использовать следующие зависимости:

(1.143)

Используя приведенные зависимости , и учитывая, что 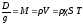,можно получить приближенные формулы для периодов свободных колебаний :

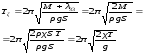(1.144)

Примем для коэффициента вертикальной полноты среднее значение χ=0,75. И учитывая, что получим следующую приближенную формулу для собственного периода вертикальной качки:

(1.145)

Для периода килевой качки с учетом (1.143), имеем:

(1.146)

Продольная метацентрическая высота H₀ мало отличается от продольного метацентрического радиуса R. Поэтому можно использовать следующую приближенную формулу:

(1.147)

Тогда с учетом формулы (1.139) будем иметь:

(1.148)

Приближенные формулы (1.145) и (1.148) показывают, что периоды килевой и вертикальной качки близки по значению. Периоды вертикальной и килевой качки увеличиваются при увеличении осадки T.

Определим приближенно период бортовой качки. Для этого будем использовать выражения (1.140) и (1.141).

(1.149)

Формула (1.149) носит название “капитанской формулы”. Из этой формулы следует, что период бортовой качки увеличивается при уменьшении метацентрической высоты h₀.

В следующей таблице приведены значения периодов бортовых и килевых колебаний некоторых типов судов.

Таблица 1.1 Собственные периоды бортовой и килевой качки некоторых типов судов

Тип судна	Период бортовой качки	Период килевой качки
Грузовые	7-12 с	4-6с
Ледоколы	6-10	3-5
Рыболовные суда	6-8	3-4
Пассажирские дедвейтом 30000-50000	20-28	10-14
Катера	3-5	2-3

Из таблицы видно, что собственные периоды бортовой качки всех типов

судов примерно в два раза больше собственных периодов килевой и вертикальной качки.