1.3 Нелинейность и нестационарность граничных условий

Основные (непреодолимые) трудности решения сформулированной задачи связаны с двумя обстоятельствами:

1. Нелинейностью граничных условий.

2. Переменностью области, в которой это решение находится.

Объединённое граничное условие на свободной поверхности нелинейно относительно производных искомой функции потенциала скорости. Динамическое условие на корпусе содержит гидромеханические силы, которые представляют собой результаты интегрирования давления по смоченной поверхности . Но давление определяется интегралом Лагранжа, которое нелинейно.

Свободная поверхность жидкости в данной задаче является взволнованной морской поверхностью, а на неё накладываются волны, вызванные движением корабля. Но характеристики данных волн неизвестны и могут быть определены только после определения потенциала скорости.

Смоченная поверхность корабля при качке также всё время меняется. Причем это изменение зависит не только от параметров волн, но и от характеристик самой качки, которые подлежат определению.

Указанные обстоятельства делают невозможным применение к сформулированной задаче использование хорошо разработанных методов решения линейных задач гидродинамики невязкой жидкости, в частности, метод распределения гидродинамических особенностей.

Для преодоления трудностей сформулированной задачи используют тривиальный путь, состоящий в полном отказе от учёта всех нелинейностей. При этом считается, что скорости движения корабля и жидкости настолько малы, что их квадратами и высшими степенями можно пренебречь. Тогда можно пренебречь соответствующими степенями производных потенциала скорости и их произведений, которые входят в граничные условия. Такой путь называется априорной линеаризацией. Однако область, в которой отыскивается решение, всё ещё остается переменной во времени. Для её упрощения, амплитуды колебаний корабля и жидкости тоже считаются относительно малыми. Тогда граничные условия можно выполнять не на действительных границах области, а на свободной поверхности жидкости и смоченной поверхности корабля в их равновесном положении. После такой линеаризации граничные условия становятся линейными, а область, в которой ищется решение неизменной во времени. В итоге характеристики движения корабля оказываются связанными с характеристиками волн линейными зависимостями.

Изучение колебаний корабля таким путем составляет суть линейной теории качки.

Более точным путем линеаризации граничной задачи является метод малого параметра. Он основан на разложении потенциала скорости движения жидкости, давления и сил, смоченной поверхности в ряды по малому параметру, в качестве которого может быть взято, например, отношение амплитуды колебаний судна к его характерному геометрическому размеру ( полуширине, осадке).

.

; (1.18)

Применение малого параметра сводит полную нелинейную задачу к последовательности линеаризированных задач. Подставляя (1.18) в общее выражение для силы и группируя составляющие при одинаковых степенях малого параметра получим :

;

; (1.19)

.

В первом приближении, кода оставлены члены, пропорциональные первой степени малого параметра, граничная задача оказывается линейной и того же типа, что и при априорной линеаризации.

Используя допущение о возможности пренебрегать всеми нелинейными членами в граничных условиях и выполнять последние на равновесных границах жидкости сформируем линейную задачу качки.

Решение уравнения Лапласа отыскивается в области, ограниченной свободной поверхностью жидкости в положении равновесия, т.е. =0 и смоченной поверхностью корпуса корабля в равновесном состоянии, уравнение которой имеет вид.

Граничное условие на свободной поверхности при исключении всех нелинейных членов будет иметь вид:

,=0. (1.20)

Граничные условия на корпусе:

, ,. (1.21)

Считая амплитуды колебаний малыми при линеаризации, получим:

Cosθ=Cosψ=Cosχ≈ 1, Sinθ ≈θ; Sinχ ≈χ; Sinψ≈ψ.

Тогда косинусы, учитывающие взаиморасположение осей систем

O₁ и Gxyz будут иметь вид (с точностью до первого порядка)

a₁=1 b₁=–χ с₁=ψ

а₂=χ b₂=1 с₂=–θ (1.22)

а₃=–ψ b₃=θ с₃≈=1.

Тогда, формулы перехода от одной системы к другой примут вид:

ξ=ξ_g+x-yχ+ψ(z-z_p);

η=η_g+xχ+y-θ(z-z_p); (1.23)

ζ=ζ_g-xψ+yθ+(z-z_p).

и

x=(ξ–ξ_g)+(η–η_g)χ–(ζ–ζ_g)ψ;

y=– (ξ–ξ_g)χ+(η–η_g)+(ζ–ζ_g)θ; (1.24)

z=z_p+(ξ–ξ_g)ψ –(η–η_g)θ+(ζ–ζ_g).

Для изучения колебательного движения необходимо перейти к первой подвижной системе координат, в которой описывается качка корабля как твердого тела. Пусть -потенциал скорости в первой подвижной системе. Тогда, учитывая формулы перехода(1.3), получим [4]:

(1.25)

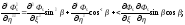(1.26)

Подставляя соответствующие производные (1.25) и (1.26) в уравнение Лапласа и в граничное условие (1.20), получим

, ζ=0; (1.27)

на Ω0=0.

Граничное условие непротекания можно расписать, представив нормальную составляющую V_n скорости произвольной точки смочённой поверхности как сумму нормальных проекций поступательной скорости движения и скорости вращения корабля вокруг оси, проходящей через полюс O.

(1.28)

где – вектор скорости точкиO –начала связанной с кораблем системы координат ,-вектор мгновенной угловой скорости, -радиус-вектор точки смоченной поверхности относительно точки O.

С учётом правила круговой перестановки:

. (1.29)

Данное условие должно выполняться при равновесном положении корабля, когда первая и вторая подвижные системы совпадают.

Проектируя выражение (1.29) на оси первой подвижной системы координат получим:

(1.30)

Обозначая:

, (1.31)

найдём

(1.32)