4. Контрольные вопросы к практической работе №6

1. Для каких целей предназначен аналого- цифровой преобразователь (АЦП)?

2. Для каких целей предназначен цифро- аналоговый преобразователь (ЦАП)?

3. В каком виде представляются входные величины в ЦАП?

4. Что составляет основу схемы ЦАП?

5. Для чего в схеме ЦАП используются переключатели?

6. Какие элементы могут использоваться в качестве переключателей?

Список литературы

_{1. Лихачев А.В. Конспект лекций. Автоматика. СПГАУ, СПБ, 2013 г..}

Раздел VIII Динамические звенья

Тема № 15 Устойчивость системы автоматики

Практическая работа №6

Оценка устойчивости САУ с помощью алгебраического критерия устойчивости Гурвица

Учебные вопросы:

1. Определение характеристического уравнения замкнутой системы, оценка выполнения необходимого условия устойчивости

2.Составление определителя Гурвица и оценка выполнения достаточного условия устойчивости.

3.Определение предельного значения коэффициента передачи системы.

1. Определение характеристического уравнения замкнутой системы, оценка выполнения необходимого условия устойчивости

Пусть известны вид и численные значения параметров разомкнутой системы автоматического управления:

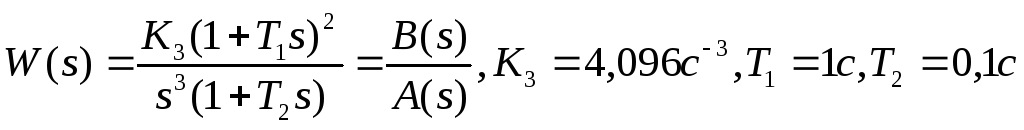
где: К₃ –коэффициент передачи системы по третьей производной (система третьего порядка астатизма);

Т₁ – постоянная времени двух форсирующих звеньев, входящих в состав системы;

Т₂ – постоянная времени апериодического звена.

Определим полиномы числителя и знаменателя в выражении передаточный функции:

B(s) = K₃(1+T₁s)²= K₁²s²+2K₃T₁S+K₃

A(s) =S³(1+T₂s) =T₂S⁴+s³

Находим полином знаменателя (характеристический полином) передаточной функции замкнутой системы:

D(s) = A(s) + B(s) = T₂s⁴ + s³ + K₃T₁²s²+2K₃T₁s+K₃.

Коэффициенты характеристического полинома:

a₄= Т₂ = 0,1 >0

a₃=1 > 0

a₂=K₃T₁² =4,096 > 0

a₁= 2K₃T₁ =8,192 > 0

a₀=K₃ =4,096 > 0

Ответ:Таким образом, необходимое условие устойчивости замкнутой системы выполняется.

2.Составление определителя Гурвица и оценка выполнения достаточного условия устойчивости.

Составляем определитель Гурвица в соответствии с известным правилами:

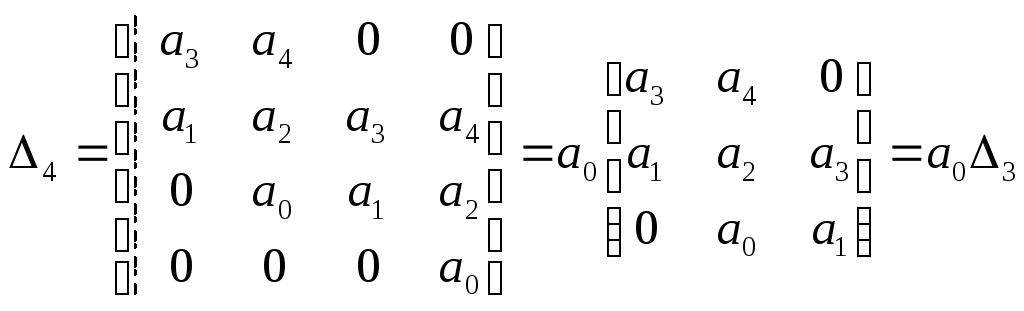
Заметим, что ранг определителя может быть понижен на единицу.

Заменим одноканальные миноры определителя Гурвица путём последовательного зачёркивания нижней строки и правого столбца.

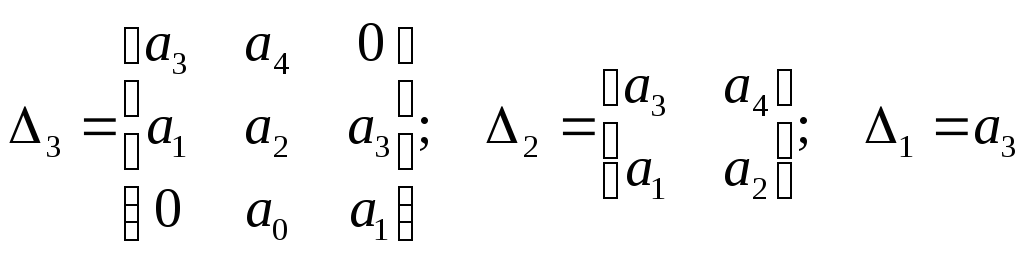
Достаточным условием устойчивости замкнутой системы является справедливость неравенств:

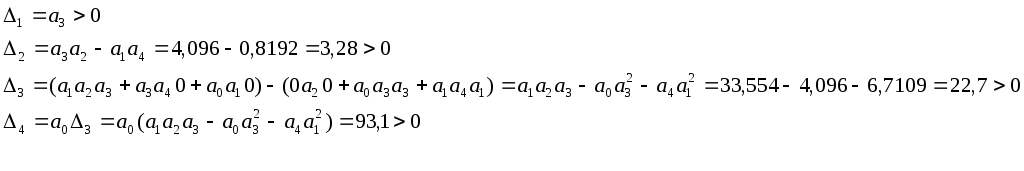
Таким образом в соответствии с критерием устойчивости Гурвица замкнутая система будет устойчива.

3.Определение предельного значения коэффициента передачи системы.

Поскольку коэффициент передачи системы К₃ =a₀входит только в одно из приведённых выше неравенств, а именно:то найти К₃пред. можно превратив это неравенство в равенство (что соответствует выходу системы на грань устойчивости).

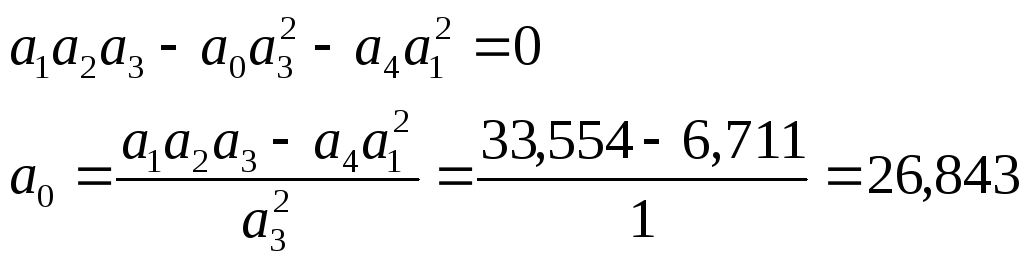
Ответ:К₃пред. = 26,843 с^-3.

Практическая работа №7

Оценка устойчивости САУ с помощью частотных критериев устойчивости

Учебные вопросы:	1. Частотный критерий устойчивости Михайлова 2.Критерий устойчивости Найквиста

1. Частотный критерий устойчивости Михайлова

Пусть имеется передаточная функция разомкнутой системы V=3 порядка астатизма (см. лекцию№19):

,

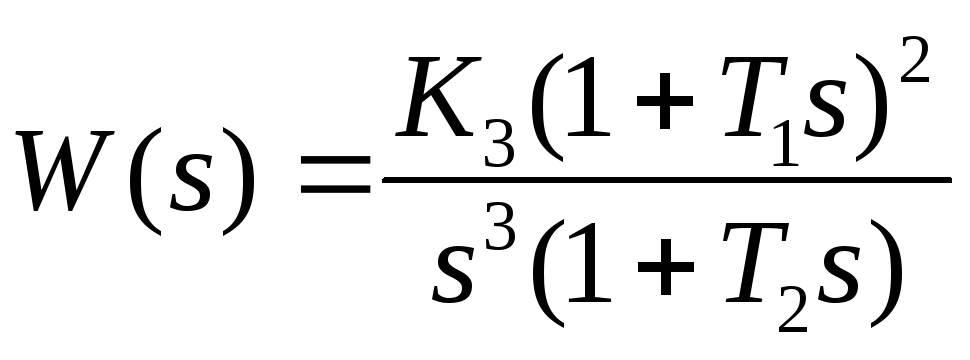
где ,,.

Запишем характеристический полином замкнутой системы:

,

где ;;;;

Для получения вектора Михайлова произведем формальную замену в выражении характеристического полинома оператора sнаjω:

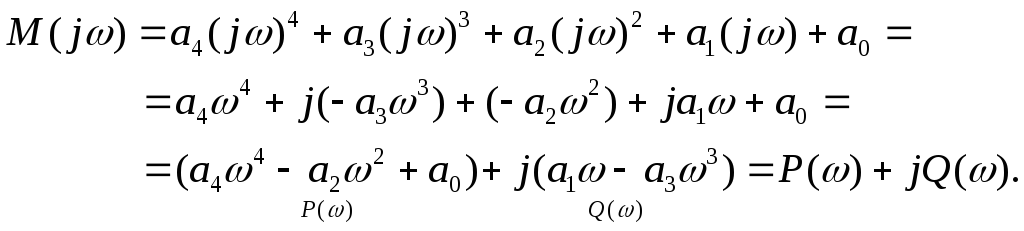
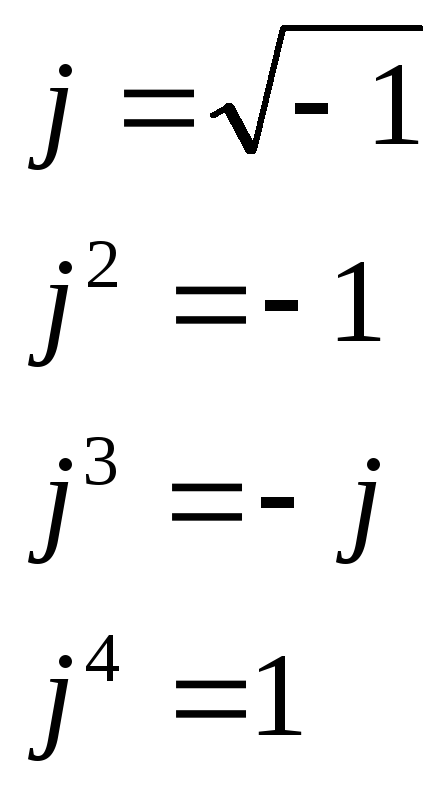
Находим корни уравнений и

;

; .

Воспользуемся IIформулировкой критерия Михайлова (условие чередуемости корней уравненийипри измененииωот0до∞)

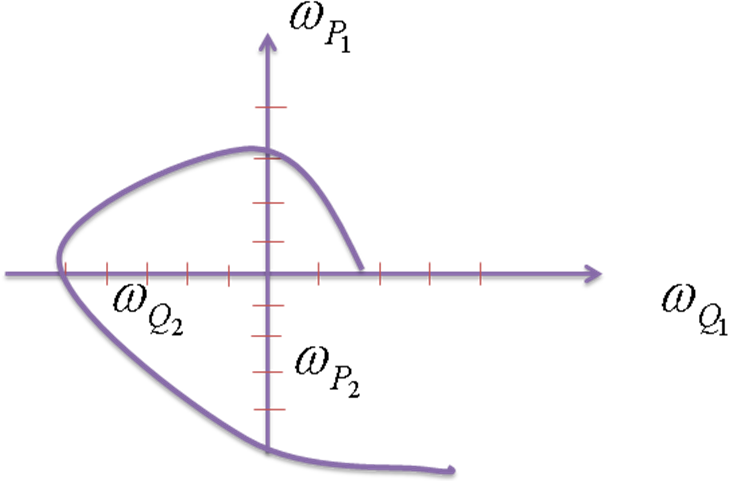
Достаточное условие устойчивости выполняется - замкнутая система будет устойчива.