
MEHANIKA
.pdf
свою первоначальную геометрическую форму. Однако как только величина q достигнет некоторого критического значения qкр , кольцо потеряет устойчивость и приобретет форму эллипса (рис. 48, б).
а
1 |
|
Pa |
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
2 |
Po |
|
3
б |
А-А |
в |
|
|
Рисунок 48
ℓр
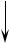 А
А
А-А
Критическое значение нагрузки qкр зависит от параметров кольца и задается формулой Блесса:
qкр |
|
3EI |
(7.20) |
|
|
r 3 |
|
|
|
ср |
|
161

Полное значение обжимающей нагрузки Qкр, приходящейся на все кольцо, может быть получено как произведение распределенной нагрузки на длину кольца:
Q q |
|
2 r |
|
6 ЕI |
(7.21) |
кр |
кр |
ср |
|
r 2 . |
|
|
|
|
ср
Сравнение полученной формулы с формулой Эйлера (5.46) показывает, что они совпадают с точностью до численного сомножителя. Роль характерного размера в одном случае играет длина стержня, а в другом – радиус кольца.
Возвращаясь к вопросу устойчивости оболочек, ограничимся рассмотрением цилиндрических обечаек, работающих под наружным давлением. Их принято делить на длинные и короткие. Длинные цилиндрические обечайки и трубы теряют устойчивость с образованием двух волн смятия, аналогично кольцам жесткости (рис. 48, б). Короткие цилиндрические обечайки теряют устойчивость с образованием трех, четырех и более волн смятия (рис. 48, в). Обечайка ведет себя как короткая, если ее длина не превосходит примерно десяти диаметров.
Пусть имеется длинная цилиндрическая оболочка с радиусом срединной поверхности rср, длиной l и толщиной стенки s. Оболочка нагружена наружным давлением р, критическое значение которого ркр требуется найти. Произведение давления на длину оболочки р l имеет размерность Н/м, такую же, как распределенная нагрузка q. Поэтому связь между критическими значениями ркр и qкр имеет вид:
qкр = ркр l или |
ркр |
|
qкр . |
|
|
|
l |
Воспользуемся формулой Блесса (7.20), выразив в последнем соотношении критическое значение распределенной нагрузки:
ркр |
|
q кр |
|
3EI |
|
l |
lrср3 . |
||||
|
|
|
Для тонкостенной цилиндрической оболочки длиной l и толщиной стенки s жесткость EI определяется формулой:
EI |
Es 3 l |
|
12 (1 2 ) , |
(7.22) |
162

где коэффициент Пуассона μ отражает взаимосвязанность колец, на которые мысленно разбита цилиндрическая оболочка. Окончательно, для величины критического давления получаем соотношение:
ркр |
4(1 |
Е |
|
s3 |
(7.23) |
|
2 ) |
|
r3 . |
||
|
|
|
|
ср |
|
При расчете на устойчивость цилиндрических обечаек вводится определенный запас устойчивости. Так что допускаемое наружное давление [p], входящее в условие устойчивости (рн ≤ [p]), связано с величиной критического давления коэффициентом запаса устойчивости nу = 2.4:
[ p] pкр / nу . |
(7.24) |
Таким образом, условие устойчивости длинной цилиндрической оболочки под действием наружного давления рн в развернутом виде может быть записано следующим образом:
|
|
Е2 |
|
|
|
s |
3 |
|
рн |
) n |
|
3 , |
(7.25) |
||||
|
4(1 |
|
y |
|
r |
|
|
|
|
|
|
|
|
ср |
|
||
откуда расчетная толщина стенки длинной цилиндрической оболочки оценивается неравенством:
s rср |
3 |
4n |
y |
(1 2 ) p |
н . |
(7.26) |
|
Е |
|||||
|
|
|
|
|
|
Потеря устойчивости коротких цилиндрических оболочек происходит с образованием трех и более волн смятия (рис. 48, в). Расчетная схема таких оболочек обычно используется для тех участков цилиндрических обечаек, которые или находятся между соседними кольцами жесткости, или заключены между фланцем корпуса и достаточно жестким днищем аппарата. На устойчивость коротких оболочек влияют условия их закрепления, а также ее длина.
Условие устойчивости для коротких цилиндрических оболочек записывается в форме, аналогичной условию (7.25):
|
|
|
|
|
|
5 |
|
|
18 10 6 Е |
rср |
|
100 s 2 |
|
||
рн |
n |
|
l |
|
2r |
|
(7.27) |
|
|
. |
|||||
|
|
y |
|
|
ср |
|
|
163

Расчетная толщина стенки короткой оболочки определяется соотношением:
|
|
|
|
|
|
|
2 |
|
|
0.94 r |
|
|
p |
|
l |
5 |
|
s |
ср |
|
|
|
|
|
||
100 |
|
10 |
6 E |
2r |
. |
(7.28) |
||
|
|
|
|
|
|
ср |
|
|
Формулы (7.25) и (7.27) используются при поверочном и нагрузочном расчетах. При этом под величиной s понимается фактическая толщина цилиндрической обечайки. Соотношения (7.26) и (7.28) используются при проектных расчетах, целью которых является определение исполнительной толщины стенки цилиндрической обечайки. В этом случае к расчетной величине, полученной в результате вычисления, следует прибавить добавку на компенсацию коррозии С1 и добавку С2 на минусовое значение предельного отклонения по толщине стального листа, из которого изготавливается элемент аппарата.
7.6. Аппараты высокого давления
Если условие тонкостенности (7.1) не выполняется, то такую оболочку называют толстостенной. Толстостенные аппараты используются для проведения технологических процессов при рабочем давлении свыше 100 атм. Поэтому такие аппараты часто называются аппаратами высокого давления. Степень толстостенности характеризуется коэффициентом β, равным отношению наружного Dн и внутреннего Dв диаметров аппарата (рис. 49): β = Dн / Dв . Для толстостенных аппаратов β > 1.1.
Для анализа напряженного состояния элементов корпуса аппаратов высокого давления расчетная схема оболочки непригодна, поскольку все три размера таких элементов сопоставимы, и следует применить расчетную схему массива. Отсюда сразу следует, что количественная оценка главных напряжений σt σm σr , вытекающая из условия тонкостенности и позволяющая пренебречь радиальным напряжением, становится несправедливой. Следовательно, в элементах корпусов аппаратов высокого давления тангенциальные, меридиональные и радиальные напряжения сопоставимы по величине. Кроме того, они меняются по толщине стенки, т. е. являются функциями радиальной координаты.
Метод мысленных сечений, построение уравнений равновесия элемента толстостенной оболочки и выкладки, во многом аналогичные тем, которые были сделаны при выводе уравнения Лапласа, позволяют получить явный вид зависимости всех трех напряжений от
164
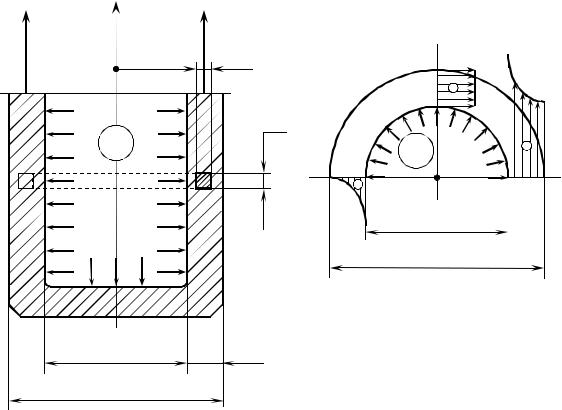
радиальной координаты в цилиндрическом толстостенном корпусе, нагруженном внутренним давлением:
а |
|
σm |
z |
|
σm |
|
б |
|
|
|
|
|
r |
|
dr |
|
|
|
σt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ σm |
|
|
|
|
|
|
dz |
|
|
|
|
|
|
P |
|
|
|
|
P |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σr |
_ |
|
О |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D1 |
D s
D1
Рисунок 49
|
|
|
|
|
|
p |
|
|
|
|
r |
2 |
|
|
||||
|
|
(r ) |
|
|
|
|
|
|
|
|
1 |
|
|
н |
|
, |
||
t |
|
|
2 |
|
|
|
|
|
2 |
|||||||||
|
|
|
|
|
1 |
|
|
r |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
m (r ) |
|
|
|
p |
|
|
, |
|
|
|
|
||||||
|
|
|
2 |
1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
p |
|
|
|
|
r |
2 |
|
|
||
|
r |
(r ) |
|
|
|
|
|
|
|
|
1 |
|
|
н |
|
|
||
|
|
2 |
|
|
|
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
r |
. |
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||
(7.29)
(7.30)
(7.31)
Здесь rн – наружный радиус оболочки.
Распределение напряжений по толщине стенки, построенное по приведенным зависимостям, иллюстрирует рис. 50. Из него видно, что в каждой точке материала наибольшим является тангенциальное напряжение, которое по мере приближения к внутренней поверхности оболочки достигает своего максимального значения (при r = rв ).
165

р(1 2 )
2 1
t
2р
2 1
р |
|
m |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 1 |
|
|
|
|
|
-p |
rв |
r |
rн |
r |
|
|
|
|
|
||
Рисунок 50
В свою очередь радиальное напряжение здесь минимально и локально уравновешивает внутреннее давление в аппарате.
Напряженное состояние материала является объемным. Поэтому при составлении условия прочности следует воспользоваться одной из гипотез прочности. Поскольку корпуса аппаратов высокого давления изготавливают из пластичных материалов, обычно используется третья гипотеза. В качестве эквивалентного напряжения принимается разность первого (наибольшего) и третьего (наименьшего) главных напряжений. В данном случае роль первого играет тангенциальное, а роль третьего – радиальное напряжения (рис. 50). Очевидно, что величина разности указанных напряжений максимальна на внутренней поверхности корпуса аппарата. Следовательно, опасна с точки зрения потери прочности именно эта область, и условие прочности должно быть составлено при r = rв. С учетом значений напряжений σt и σr (см. рис. 50) имеем:
экв = σt (rв ) - σr (rв ) = |
2 |
р |
2 |
, |
(7.32) |
|
|
|
|
|
|||
|
2 |
1 |
||||
|
|
|
|
|||
где - коэффициент прочности сварного шва. Справедливость этого неравенства подтверждается при поверочном расчете, когда известны все входящие в него величины. При нагрузочном расчете оно
166

решается относительно р с целью определения допускаемого давления. Наконец, при проектном расчете неравенство (7.32) следует решить относительно коэффициента толстостенности :
|
|
|
[ ] |
|
|
|
|
[ ] 2 p . |
(7.33) |
||||||
|
|
||||||
Зная величину , нетрудно найти толщину стенки s, поскольку они связаны простым соотношением:
s = rн – rв = rв ( - 1). |
(7.34) |
Внутренний радиус rв определяется производительностью аппарата и обычно известен.
Из формул (7.33) и (7.34) вытекает важный вывод. Если увеличивать давление в аппарате, то при р / 2 коэффициент и толщина стенки стремятся к бесконечности. Это значит, что при таких предельных значениях внутреннего давления никаким увеличением толщины стенки нельзя добиться работы сосуда в области упругих деформаций.
Оценим численно величину таких предельных давлений для корпусов из высокопрочных сталей, для которых допускаемое давление составляет величину порядка 400 МПа. Принимая коэффициент прочности сварного шва равным единице, получаем
рпред = 200 МПа = 2000 атм. Однако ряд промышленных процессов (например, полимеризация этилена, процессы прессования) требуют
рабочих давлений, превышающих это значение.
На практике широко используются несколько методов повышения внутреннего давления в толстостенных корпусах технологических аппаратов. Один из них основан на применении многослойных цилиндрических оболочек, в которых на стадии изготовления создаются предварительные (сборочные) напряжения. При подаче внутреннего давления в сосуд за счет сборочных напряжений обеспечивается снижение рабочих напряжений от давления в наиболее нагруженных внутренних слоях и одновременно некоторое повышение этих напряжений в слабонагруженных наружных слоях материала.
7.7.Контрольные вопросы
1.Какие аппараты и сосуды считаются тонкостенными? Какие процессы проводятся в таких аппаратах?
167
2.Каким условиям должны удовлетворять геометрические размеры элемента оборудования, чтобы к нему была применима расчетная схема оболочки?
3.Перечислите типовые оболочки вращения, которые используются при изготовлении химико-технологических аппаратов.
4.Назовите основные геометрические характеристики оболочек вращения.
5.Что такое первый и второй главные радиусы кривизны?
6.Какие оболочки относятся к осесимметричным?
7.Чему равны главные радиусы кривизны типовых оболочек вращения?
8.Какие напряжения возникают в тонкостенных оболочках, нагруженных внутренним давлением?
9.Что такое линии искажения? Какова картина напряженного состояния материала в их окрестности?
10.Запишите уравнение Лапласа. Каков его физический смысл?
11.Почему недостаточно одного уравнения Лапласа для анализа напряженного состояния типовых оболочек?
12.Запишите дополнительное уравнение к уравнению Лапласа.
13.Почему в тонкостенных оболочках напряжением в радиальном направлении пренебрегают?
14.Какое из двух напряжений (меридиональное или тангенциальное) больше в корпусах аппаратов?
15.Как составляется условие прочности для типовых оболочек?
16.Каков физический механизм возникновения напряжений в плоских оболочках (пластинах)?
17.Запишите условие прочности для плоских днищ и крышек аппаратов.
18.Какая из типовых оболочек будет иметь большую толщину при одном и том же значении внутреннего давления?
19.Что такое устойчивость оболочек? С чем может быть связана потеря их устойчивости?
20.Что такое критическое значение наружного давления?
21.Чем отличаются длинные и короткие цилиндрические оболочки? Как ведут себя при потере устойчивости те и другие?
22.От каких параметров зависит величина критического давления для длинных и коротких оболочек?
23.Какие аппараты и сосуды считаются толстостенными? Какие процессы проводятся в таких аппаратах?
24.Какие напряжения возникают в толстостенных оболочках и как они меняются по толщине стенки?
25.Какое из напряжений является наибольшим?
26.Запишите условие прочности для толстостенных оболочек.
168
8. ДЕТАЛИ, УЗЛЫ И МЕХАНИЗМЫ МАШИН И АППАРАТОВ
Простейшим элементом конструкции механизма, машины или аппарата является деталь – элемент, изготовленный из цельной части материала без использования сборочных операций, например,
таких как сварка, пайка, запрессовка и др. По функциональному признаку детали разделяются на несколько групп:
-крепежные (болты, винты, шпильки, гайки, заклепки, штифты и т.п.);
-детали механизмов (валы, зубчатые колеса, шкивы, рычаги и т.п.);
-детали направляющих (элементы подшипников);
-детали герметизирующих устройств (фланцы, прокладки и т.п.);
-корпусные детали (станины, обечайки, днища, крышки и т.п.);
-упругие элементы (пружины, сильфоны, мембраны и т.п.);
-детали рабочих органов или исполнительных устройств (диски, лопасти, ступицы и т.п.);
-вспомогательные детали (рукоятки, петли люков и крышек, смотровые стекла и т.п.).
Как отмечалось выше, различные по назначению детали могут иметь одинаковую расчетную схему и рассчитываться с целью обеспечения их работоспособности по одинаковым методикам.
Конструкции механизмов машин и аппаратов состоят из узлов или сборочных единиц, т.е. подвижно или неподвижно соединенных между собою деталей. Подвижные соединения являются конструктивным исполнением кинематических пар механизмов (шарниры, винтовые пары и т.п.), обеспечивающих целенаправленные движения звеньев. Неподвижные соединения предназначены для разделения конструкции на составные части, что позволяет упростить изготовление и сборку изделия. Под термином «соединение деталей» понимают неподвижные соединения, в которых детали после сборки не имеют возможности относительного перемещения.
Вконструкциях самых разных машин и аппаратов очень часто для выполнения одинаковых или различных функций применяются однотипные механизмы, т.е. механизмы, имеющие одинаковую структуру (устройство) и различающиеся лишь своим масштабом, кинематическими и энергетическими параметрами.
Качество машин, аппаратов и приборов во многом зависит от качества входящих в их состав деталей, а также от вида и качества соединений.
8.1. Основные типы неразъемных и разъемных соединений
Наиболее распространенные соединения разделяют на две основные группы: неразъемные и разъемные (см. таблицу).
Неразъемные соединения – соединения, разборка которых возможна лишь в результате разрушения или повреждения конструктив-
169

ных элементов детали. Неразъемные соединения часто выполняют функции цельноизготовленной детали, если ее получение технологически затруднительно или неэкономично. Неразъемные соединения компактнее разъемных, однако, затруднен контроль качества этих соединения.
Таблица. Классификация |
Разъемные соединения – со- |
|||
единения, которые позволяют осу- |
||||
основных типов соединений |
||||
ществлять многократную сборку и |
||||
|
|
|||
|
разборку конструкции при сохра- |
|||
Типы соединений |
||||
|
|
нении формы и размеров деталей. |
||
Неразъемные |
Разъемные |
|||
|
|
Применение |
в проектируе- |
|
- сварные; |
- резьбовые; |
|||
- пайкой; |
- шпоночные; |
мом оборудовании того или иного |
||
- адгезивами; |
- шлицевые; |
типа соединения |
определяется |
|
- заформовкой; |
- штифтовые; |
особенностями функционирования |
||
- склепыванием; - фланцевые; |
и изготовления конструкции или |
|||
- вальцеванием; - байонетные; |
ее узлов, а также возможностями |
|||
- запрессовкой |
- профильные |
производства, экономическими по- |
||
казателями и пр. Основными критериями работоспособности, которым должны отвечать соединения – прочность, жесткость, виброустойчивость, плотность (т.е. способность защищать рабочую поверхность изделия от проникновения твердых посторонних частиц), герметичность (т.е. способность препятствовать прохождению жидкости или газа через стык соединения).
8.2.Неразъемные соединения
1)Сварные соединения – наиболее распространенный вид неразъемных соединений. Сварка – технологический процесс, основанный на образовании межатомных связей между материалами соединяемых деталей. Сварка может производиться, во-первых, за счет сильного местного нагрева деталей до расплавленного состояния и последующего остывания (сварка плавлением) и, во-вторых, при совместном пластическом деформировании нагретых или холодных стыков деталей (сварка давлением). Затвердевший после сварки материал, соединяющий сваренные детали, образует сварной шов или
сварную точку.
Сварка плавлением. К сварке плавлением относятся следующие виды: дуговая сварка, газовая, плазменная, электрошлаковая, электронно- и ионнолучевая и др.
Наиболее распространенной является дуговая сварка, при которой в качестве источника тепла используется электрическая дуга. Дуговая сварка может быть осуществлена плавящимся и неплавящимся (угольными, графитовыми или вольфрамовыми) электродами. Она может выполняться вручную, автоматически или полуавтоматически (с механизированной подачей только электродной проволоки). Для
170
