MEHANIKA

В моменты времени, соответствующие переходу точки через ось Оу, проекция скорости Vx = - ak для четных значений i, Vx = ak для нечетных i . Проекция Vу = 0 в обоих случаях. Следовательно, вектор скорости точки М в эти моменты времени параллелен оси Ох.

Ускорение точки определим, дифференцируя выражения для проекций скорости по времени:

В моменты времени, соответствующие переходу точки через ось Оу, проекция Wx =0, а проекция Wу = -bk2 для четных значений i, Wу = bk2 для нечетных i. Следовательно, в указанные моменты времени ускорение направлено к центру эллипса по главной нормали к траектории движения точки М.

3.3. Поступательное и вращательное движение твердого тела

Поступательным движением твердого тела называется такое движение, при котором любая прямая, связанная с телом, перемещается в пространстве, оставаясь параллельной самой себе. Другими словами, при поступательном движении отсутствуют какиелибо повороты тела. Покажем, что при таком характере движения все точки тела двигаются по идентичным траекториям, в каждый момент времени имеют одинаковые скорости и ускорения.

Выберем в движущемся теле две произвольные точки А и В (рис. 16). Их положение определяется радиус-векторами rА и rВ, которые меняются с течением времени. Пусть r – вектор с началом в точке А и концом в точке В.

В rB

rА

А

Рисунок 16

41

Векторы rА , rВ и r в любой момент времени связаны соотношением: rВ = r + rА. Если тело движется поступательно, то, согласно определению, r = const. С учетом этого продифференцируем векторное равенство по времени:

т. е. скорости точек А и В одинаковы как по величине, так и по направлению в любой момент времени. Дифференцируя вторично, убеждаемся, что и ускорения точек также одинаковы. Следовательно, поступательное движение твердого тела полностью определяется движением одной из его точек. Другими словами, кинематика поступательного движения твердого тела сводится к кинематике точки. Поэтому все положения подразделов 3.1 и 3.2 применимы для описания этого типа движения тела.

Еще одним простейшим типом движения твердого тела является

вращательное движение. При вращательном движении все точки тела, лежащие на некоторой прямой, остаются неподвижными во все время движения. Указанная прямая называется осью вращения. Точки тела, не лежащие на оси вращения, движутся в плоскостях, перпендикулярных оси вращения, по окружностям с центром на оси. Их положение в произвольный момент времени однозначно определяется углом φ поворота тела относительно некоторой фиксированной неподвижной плоскости, проходящей через ось вращения. Угол поворота принято считать положительным, если вращение происходит против часовой стрелки, и отрицательным – в противном случае. При вращении угол поворота тела меняется во времени:

Это уравнение служит уравнением вращательного движения

твердого тела.

Кинематическими характеристиками вращательного движения являются угловая скорость и угловое ускорение. Угловой скоростьюназывается вектор, лежащий на оси вращения. Модуль этого вектора, характеризует быстроту изменения угла поворота во времени:

42

Направление вектора угловой скорости выбирается так, чтобы вращение происходило против часовой стрелки, если смотреть с конца вектора . Единица измерения угловой скорости – радиан в секунду (рад / с или с-1). В технике часто используется другая единица измерения – обороты в минуту n (об / мин). Их связывает простое соотношение: = n / 30.

Угловое ускорение также изображается вектором, лежащим на оси вращения. Модуль вектора характеризует быстроту изменения угловой скорости во времени:

Направление вектора углового ускорения совпадает с направлением вектора угловой скорости , если движение тела ускоренное, и противоположно ему, если движение замедленное. Верно и обратное утверждение.

В зависимости от значений кинематических характеристик и различают следующие частные случаи вращательного движения твердого тела.

При равномерном вращательном движении угловое ускорение ε

= 0. Тогда, согласно (3.23), движение происходит с постоянной угловой скоростью: ω = const. Интегрирование (3.22) приводит к уравнению равномерного вращательного движения тела: φ( ) = φ0 + ω .

При равнопеременном вращательном движении угловое ускорение ε = const. Дважды интегрируя (3.23), приходим к уравнению равнопеременного вращательного движения: φ( ) = φ0 + ω0 + 0,5 ε 2. В приведенных формулах через φ0 и ω0 обозначены значения угла поворота и угловой скорости при = 0.

Угловая скорость и угловое ускорение являются кинематическими характеристиками тела в целом, а не его отдельных точек. Для того чтобы найти скорости и ускорения точек при вращательном движении, необходимо применить положения предыдущего параграфа.

Траектория любой точки тела при его вращении представляет собой окружность, которая лежит в плоскости, перпендикулярной оси вращения. Центр окружности находится на оси, а ее радиус равен расстоянию от оси до данной точки. Поскольку траектория точки известна, целесообразно применить естественный способ задания ее движения. Дуговую координату s будем отсчитывать вдоль дуги окружности в направлении положительного изменения угла поворота. Тогда угол поворота и дуговая координата связаны между собой известным соотношением: s = R . Согласно (3.9), модуль скорости точки равен:

43

т. е. величина скорости точек вращающегося тела пропорциональна их расстояниям до оси вращения и угловой скорости. Направление вектора скорости совпадает с направлением касательной к окружности – траектории точки.

Ускорение точки при естественном способе задания движения в соответствии с (3.15) является суммой двух ускорений: касательного и нормального. Величина касательного ускорения определяется формулой (3.16). Для рассматриваемого кругового движения точки она равна:

Величину нормального ускорения можно найти с помощью соотношения (3.17). Для рассматриваемого случая она равна:

Модуль полного ускорения найдем, используя (3.18):

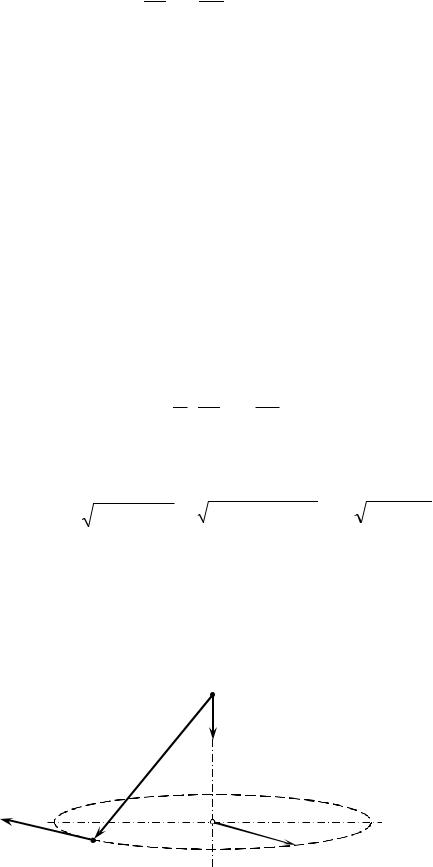
Выведенные формулы допускают более общую запись с помощью операций векторной алгебры. Поместим начало координат в произвольную точку оси вращения (рис. 17). Тогда положение некоторой точки М вращающегося тела определяется радиусвектором r. Модуль радиус-вектора r и расстояние точки М до оси

O

r

V

M R

Рисунок 17

44

связаны простым соотношением: R = r sin (r,ˆ ). С учетом (3.24) для модуля скорости точки М получим выражение: V = r sin (r,ˆ ), из которого следует, что вектор V является векторным произведением векторов r и (рис. 17):

Полученная формула носит название формулы Эйлера. Она позволяет определить скорость любой точки вращающегося тела и поэтому играет важнейшую роль в кинематике.

Дифференцирование равенства (3.28) по времени с учетом свойств векторного произведения и соотношений (3.5), (3.10), (3.15) и (3.23) позволяет записать:

Сравнение полученного соотношения с (3.15) показывает, что первое слагаемое представляет собой касательное ускорение Wm, а второе – нормальное Wn. Таким образом, при вращательном движении тела проекции полного ускорения его точек на направления касательной к траектории и нормали в общем случае определяются с помощью следующих формул:

Касательное ускорение иногда называют вращательным, а нормальное ускорение – центростремительным. Полное ускорение точки в соответствии с (3.15) равно сумме векторов Wm и Wn.

3.4. Плоскопараллельное движение твердого тела

Следующим по сложности после поступательного и вращательного движения твердого тела является плоскопараллельное движение.

Плоскопараллельным (или плоским) движением называется движение, при котором все точки тела перемещаются в плоскостях, параллельных некоторой неподвижной плоскости. При таком характере движения тела его количественное описание сводится к описанию движения одного сечения тела, параллельного указанной неподвижной плоскости. Это сечение обычно называют плоской фигурой. Следовательно, для того чтобы получить кинематические характеристики при плоскопараллельном движении тела достаточно рассмотреть скорости и ускорения точек плоской фигуры при ее движении в собственной плоскости.

45

Пусть на плоской фигуре зафиксирована некоторая точка Р – полюс (рис. 18). Положение этой точки в неподвижной системе координат Оху однозначно определяется ее координатами хР и уР – координатами полюса. Координаты других точек плоской фигуры будут зависеть как от положения полюса Р, так и от угла поворота плоской фигуры вокруг полюса. При движении тела все три величины хР , уР и являются функциями времени:

у

у

х

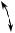
Р

Эти зависимости называются уравнениями плоскопараллельного движения. Они показывают, что плоское движение представляет собой наложение двух одновременно происходящих уже рассмотренных ранее движений тела: поступательного и вращательного. Следовательно, основными кинематическими характеристиками при этом типе движения являются скорость и ускорение полюса Р (поступательная часть движения) и угловая скорость и угловое ускорение тела (вращательная часть движения). Причем первые две характеристики зависят от выбора полюса, а две вторые от выбора полюса не зависят.

Пусть уравнения (3.31) заданы. Выведем соотношения, позволяющие определить скорость произвольной точки М плоской фигуры. Положению точки М в некоторый момент времени отвечает радиус-вектор rМ в неподвижной системе координат Оху, положению полюса Р отвечает радиус-вектор rР. Оба радиус-вектора при движении тела могут меняться как по величине, так и по направлению. Точки Р и М соединим вектором rМР с началом в полюсе Р и концом в точке М. Поскольку расстояние между точками М и Р фиксировано, вектор rМР при движении плоской фигуры может меняться во времени

46

только по направлению, т. е. положение точки М относительно полюса

Рможет измениться только за счет вращения плоской фигуры.

Влюбой момент времени будет выполняться векторное равенство:

rМ = rР + rМР

Дифференцирование этого равенства по времени позволяет записать:

т. е. скорость любой точки твердого тела при плоскопараллельном движении равна векторной сумме скорости полюса и скорости, которую имеет эта точка в относительном вращении вокруг полюса.

Направление и величина вектора VMP определяются по соотношениям для вращательного движения: направление скорости VMP в любой момент времени перпендикулярно отрезку МР по ходу вращения плоской фигуры, а модуль скорости VMP равен произведению угловой скорости и длины отрезка МР.

Оказывается, что в каждый момент времени одна из точек плоской фигуры имеет скорость равную нулю. Эта точка называется

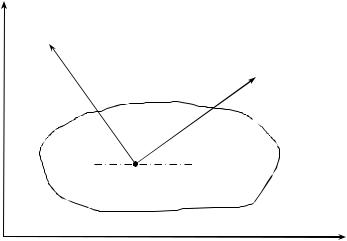
мгновенным центром скоростей. Пусть, например, в некоторый момент времени плоская фигура имеет угловую скорость ω, а одна из ее точек – точка А – скорость VА. Через точку А проведем луч, перпендикулярный вектору VА, и на этом луче выберем точку В, отстоящую от точки А на расстоянии |АВ| = VА / ω (рис.19).

Рисунок 19

Применим теперь для точки В соотношение (3.32), взяв в качестве полюса точку А:

VВ = VА + VВА

Скорость VВА точки В, обусловленная вращением плоской фигуры, равна по модулю |АВ| ω = VА и направлена в противоположную сторону. Следовательно, правая часть предыдущего векторного

47

равенства обращается в нуль, а точка В в данный момент времени является мгновенным центром скоростей.

Приведенное несложное построение позволяет сделать несколько важных выводов. Во-первых, мгновенными центрами скоростей в различные моменты времени служат разные точки плоской фигуры. Во-вторых, мгновенный центр скоростей может находиться в некоторой точке пространства за пределами твердого тела. Наконец, в-третьих, возможны случаи, когда в какой-то момент времени угловая скорость плоской фигуры равна нулю. При этом мгновенный центр скоростей оказывается удаленным в бесконечность. Эти случаи соответствуют так называемому мгновенному поступательному движению, когда скорости всех точек тела в данный момент времени векторно равны.

Если в качестве полюса выбрать мгновенный центр скоростей, то первое слагаемое в (3.32) обратится в нуль. Следовательно, скорость любой точки тела будет определяться только скоростью ее вращательного движения вокруг мгновенного центра скоростей. Величина скорости будет пропорциональна расстоянию от данной точки до мгновенного центра скоростей, а ее направление будет перпендикулярно линии, соединяющей точку и цент скоростей.

В силу очевидной важности понятия мгновенного центра скоростей рассмотрим несколько способов определения его местонахождения.

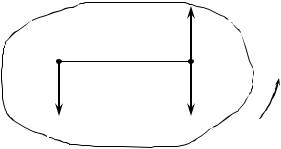
Рисунок 20

Если в некоторый момент времени известны угловая скорость вращения плоской фигуры и скорость одной из ее точек, то положение мгновенного центра скоростей С в этот момент времени можно найти с помощью построения, проведенного выше при доказательстве его существования.

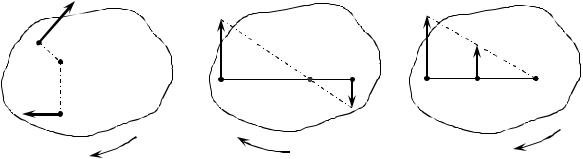
Если известны направления скоростей двух точек А и В и они не параллельны друг другу, то положение центра скоростей С определяется пересечением перпендикуляров, восстановленных к скоростям в этих точках (рис. 20, а). В случае если скорости в точках А и В известны и параллельны, необходимо выполнить несложные

48

построения, показанные на рис. 20, б, в . Случай VВ = VА соответствует мгновенному поступательному движению.

Для вывода соотношения, позволяющего найти ускорение точек при плоскопараллельном движении тела, необходимо продифференцировать равенство (3.32) по времени:

dVM dVP dVMP .

d d d

В левой части равенства стоит ускорение WM рассматриваемой точки М, которое представляет собой сумму ускорения полюса WР в поступательной части движения плоской фигуры (первое слагаемое правой части) и ускорения WMР точки М во вращательном движении плоской фигуры вокруг полюса Р (второе слагаемое): WM = WР + WМР. Ускорение WР находится с помощью соотношений, полученных при рассмотрении поступательного движения твердого тела, а ускорение WМР равно векторной сумме касательного и нормального ускорений во вращательном движении вокруг полюса (формулы (3.25) и (3.26)).

3.5. Скорость и ускорение точки при сложном движении

До сих пор рассматривались кинематические характеристики движения только в неподвижной системе координат. Однако, зачастую возникает необходимость определить характеристики движения отдельных точек твердого тела в системе координат, которая сама перемещается относительно неподвижной системы координат. Еще одна важная задача – установить связь между кинематическими характеристиками движения точки (траекториями, скоростями и ускорениями) в подвижной и неподвижной системах координат.

Пусть имеются две системы координат: неподвижная Охуz и подвижная О1х1у1z1. Движение точки М относительно неподвижной системы координат Охуz называется ее абсолютным движением. Соответственно говорят о скорости Va и ускорении Wa в абсолютном движении. Движение точки М относительно подвижной системы координат О1х1у1z1 носит название относительного движения, а скорость Vr и ускорение Wr в относительном движении называются относительной скоростью и относительным ускорением. Движение подвижной системы координат относительно неподвижной называется переносным движением. Для количественной характеристики переносного движения используются понятия переносной скорости

Vе и переносного ускорения Wе. По определению это скорость и ускорение той точки подвижной системы координат, с которой в данный момент совпадает точка М.

Для лучшего понимания введенных понятий рассмотрим качение без скольжения колеса по полотну дороги (рис. 21). Точка М обода

49

колеса в системе координат О1х1у1, связанной с колесом, движется по окружности. Это движение является относительным. Переносным

уу1

М

О1 х1

Рисунок 21

движением (движением подвижной системы координат относительно неподвижной) в этом примере является поступательное движение. В самом деле, точка подвижной системы координат, которая совпадает в данный момент времени с точкой М, будет двигаться прямолинейно параллельно оси Ох вместе с центром колеса. В неподвижной системе координат точка М будет совершать сложное движение, траекторией которого будет циклоида.

Из приведенного примера видно, что абсолютное движение точки можно рассматривать как наложение двух или более движений, которые, как правило, являются более простыми для изучения. Поэтому важно знать связь между кинематическими характеристиками абсолютного, переносного и относительного движений, чтобы по известным кинематическим характеристикам последних найти кинематические характеристики абсолютного движения.

Для установления такой связи рассмотрим две системы координат: неподвижную Охуz и подвижную О1х1у1z1. Пусть r – радиус-вектор точки М в неподвижной системе координат, а - радиус-вектор этой же точки в подвижной системе координат. В любой момент времени указанные вектора связаны соотношением:

r = r0 +

где r0 – радиус-вектор начала подвижной системы координат в системе координат Охуz. Продифференцируем это равенство по времени:

50