1. Предел функции в точке. Предел в бесконечно удаленной точке. Замечтельные пределы.

Пусть произвольное фиксированное число.

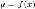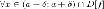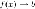а)Пусть задано некоторое числовое множество и каждому поставлено в соответствие число , тогда говорят, что на множестве задана функция , .Число называется пределом функции в точке , если для такое, что для из того, что следует, что : или при .

б) Будем говорить, что переменная x стремится к бесконечности, если для каждого заранее заданного положительного числа M (оно может быть сколь угодно большим) можно указать такое значение х=х₀, начиная с которого, все последующие значения переменной будут удовлетворять неравенству |x|>M.

Будем говорить, что функция f(x) стремится к пределу b при x → ∞, если для произвольного малого положительного числа ε можно указать такое положительное число M, что для всех значений x, удовлетворяющих неравенству |x|>M, выполняется неравенство |f(x) - b| < ε. Обозначают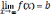

4

1 и 2 замечательные пределы. 1 замечательный предел: lim (sinx)/x =1 при x->0.П:(x->0) lim((1-cosx)/x(sqrt(1+x)-1))=lim(2sin²(x/2)*(sqrt(1+x)+1)/x(sqrt(1+x)-1)(sqrt(1+x)+1))= lim(2sin²(x/2)/x²)*lim (sqrt(1+x)+1) =(1/2)*2=1. 2 замечательный предел: lim (1+x)^1/X = e при x0. П:(n->¥) lim(1+3/n)ⁿ=e³.

Первый замечательный предел

Доказательство: докажем для справедливость неравенства

В силу четности входящих в неравенство ф-ий, докажем это неравенство на промежутке

площадь кругового сектора

, так как х>0, то ,

2. следовательно, что

1. Покажем, что

2. Докажем, что

3. Последнее утверждение:

18. Второй замечательный предел

lim(n)(1+1/n)^n=e Док-во:

x+ n x:n=[x] => nx<n+1 => 1/(n+1)<1/x<1/n

Посколько при ув-нии основания и степени у показательной ф-ции, ф-ция возрастает, то можно записать новое неравенство (1/(n+1))^n(1+1/n)^x (1+1/n)^(n+1) (4)

Рассмотрим пос-ти стоящие справа и слева. Покажем что их предел число е. Заметим (х+, n)

lim(n)(1+1/(n+1))=lim(n)(1+1/(n+1))^n+1-1= lim(n)(1+1/(n+1))^n+1lim(n)1/(1+1/(n+1))=e

lim(n)(1+1/n)^n+1= lim(n)(1+1/n)^n lim(n)(1+1/n)=e1=e

ВОПРОС№2

Число e. На основании Т Вейерштрасса (всякая монотонная ограниченная последовательно-сть имеет предел) последовательность x_n=(1+1/n)ⁿ, nÎN, имеет предел, обозначаемый обыч-но буквой е: lim(1+1/n)ⁿ при n->¥ =e. Число е называют неперовым числом. Оно иррациона-льное,приближённо равно 2,72.Число е принято за основание натуральных логарифмов: ло-гарифм по основанию е называется натуральным логарифмом.

. Число е

Рассмотрим числ. посл-ть с общим членом xn=(1+1/n)^n (в степени n)(1) . Оказывается, что посл-ть (1) монотонно возр-ет, ограничена сверху и сл-но явл-ся сходящейся, предел этой пос-ти наз-ся экспонентой и обозначается символом е2,7128…

Док-ем формулу lim(n->∞)(1+1/n)^n(в степени n)=е

y_N=; z_N=y_N +

1) y_N монотонно растет

2) y_N<z_N

3) z_N-y_N0

4) z_N монотонно убывает

Доказателство:

z_N-z_N+1 = y_N +- y_N+1 -=+-=

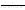2=y₁<y_N<z_N<z₁=3

e = Lim y_N = Lim z_N - по лемме о вложенных промежутках имеем: y_N<e<z_N = y_N + 1/(n*n!)

Если через _ обозначить отношение разности e - y_N к числу 1/(n*n!), то можно записать e - y_N =_/(n*n!), заменяя y_N его развернутым выражением получаем e = y_N + _/(n*n!), (0,1)

Число e иррационально:

Доказательство(от противного): Пусть e=m/n, mZ, nN

m/n = e = y_N + _/(n*n!)

m*(n-1)!= y_N*n! + _/n, где (m*(n-1)! & y_N*n!)Z, (_/n)Z => противоречие

а) если в т-ке х0  оба односторонних предела, которые совпадают между собой f(x0+)= f(x0-), но  f(x0), то такая т-ка наз-ся точкой устранимого р-рыва.

Если х0 т-ка устранимого р-рыва, то можно перераспределить ф-цию f так чтобы она стала непр. в т-ке х0. Если по ф-ции f построить новую ф-цию положив для нее знач. f(x0)= f(x0-)=f(x0+) и сохранить знач. в др. т-ках, то получим исправл. f.

б) если в т-ке х0  оба 1-стороних предела f(x0), которые не равны между собой f(x0+)f(x0-), то х0 наз-ся т-кой р-рыва первого рода.

в) если в т-ке х0 хотя бы 1 из односторонних пределов ф-ции не  или бесконечен, то х0 наз-ся т-кой р-рыва 2-го рода.

2. Односторонние пределы. Теорема о существовании предела функции в точке.

Односторонний предел – предел числовой функции , подразумевающий приближение к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым.

Теорема  (теорема "о двух милиционерах")   Пусть даны три функции ,и, при всехиз некоторого окончаниябазысвязанные неравенством

Пусть функции иимеют общий предел при базе:

Тогда функция также имеет предел при базе, равный тому же числу:

Доказательство.     Согласно определению предела, для любого найдутся такие окончания базыи, что привыполняется неравенство

а при -- неравенство

Значит, для окончания при всехвыполняются неравенства

то есть

Это означает, что предел величины равен.

Рис.2.21.Два милиционера ии пьяныйдвижутся в участок

ВОПРОС№3. Предел функции в точке. Единственность предела.

1)Число называетсяпределом функции в точке , если для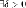такое, что для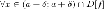из того, чтоследует, что:илипри.

2) Теорема о единственности предела

Формулировка:

Если функция в точкеимеет предел, то этот предел единственный.

Доказательство:

Докажем методом от противного. Предположим, что ,,. Возьмём, по определению и свойству окрестности найдётся такая проколотая-окрестность точки(), в которой одновременно будут выполнятся неравенства,, тогда в точках этой же окрестности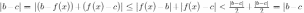. Получили противоречие. Отсюда, функцияв точкеимеет единственный предел.

ВОПРОС№4. Бесконечно большие и бесконечно малые.Свойства бесконечно малых.

1) Функция называетсябесконечно малой функцией (б.м.ф.) при (или в точке), если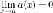

Б-м и б-б пос-ти: опр, осн. Св-ва, связь между ними

Пос-ть Xn н-ся б-б, если для любого положительного числа А существует номер N такой, что при всех n>N выполняется нер-во |Xn|>A, т.е. (A>0)(N=N(A))(n>N):|Xn|>A Любая б-б пос-ть явл. неограниченной. Однако неограниченная пос-ть может и не быть б-б.

Пос-ть {An} н-ся б-м, если для любого положительного числа ε (сколь бы малым мы его ни взяли) существует номер N=N(ε) такой, что при всех n>N выполняется нер-во |An|< ε, т.е. (ε>0)(N=N(ε))( n>N):|An|< ε

Св-ва: 1.Если {Xn} б-б пос-ть и все ее члены отличны от нуля, то по-сть {1\Xn} б-м и обратно. 2.Сумма и разность двух б-м пос-тей есть б-м пос-ть. (следствие: алгебраическая сумма любого конечного числа б-м постей есть б-м пость.) 3.Произведение двух б-м постей есть б-м пость.4. Произведение ограниченной пости на бесконечно малую пость есть пость б-м.

Бесконечно малые последовательности. О: Посл-ть а_N называется бесконечно малой (бм) если ее предел равен нулю (Е>0  n₀: n>n₀ |а_N|<Е). Т: Сумма (разность) бм послед-тей является бм послед-тью. Т: Произведение бм и огр-ной послед-ти - бм послед-сть. Д: Пусть a_N - бм посл-ть, b_N - ограниченная посл-ть; z_N=a_N*b_N. Т.к. b_N – огр-ная посл-ть, значит  такое с: |b_N|с0. Т.к. a_N - бм посл-ть, значит вне любой Е-окрестности точки 0 (в частности Е/с)лежит конечное число членов посл-ти a_N, т.е.  n₀: n>n₀ |a_N|<Е/с.Таким образом n>n₀: |z_N|=|a_N*b_N|=|a_N|*|b_N|<Е/с * с=Е. С: произведение бм посл-тей - тоже бм посл-ть. Т: Пусть a_N - бм. Еслиn’: n>n’ послед-сть |b_N|a_N => b_N – бм. Д: a_N - бм =>  n”: n>n”: |a_N|<Е. Для n>=max{n’,n”} |b_N||a_N|<Е.

2)Теорема 1. Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.

Доказательство. Пусть – бесконечно малая последовательность. Это означает, что для любого положительного числасуществует такой номерN, что для всех номеров выполняется условие, гдеС – любое действительное число. Тогда <

< , а это и означает, что последовательность– бесконечно малая.

Теорема 2. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Доказательство. Пусть и– бесконечно малые последовательности. Это означает, что для любого числасуществуют такие номераи, что для всех номерови для всех номероввыполняются условияисоответственно. Тогда для всех номероввыполняется условие, а это и означает, что последовательность– бесконечно малая.

Следствие 1. Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Следствие 2. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Теорема 3. Бесконечно малая последовательность ограничена.

Доказательство. Пусть 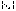– бесконечно малая последовательность,ε>0 – некоторое число, а N – номер, начиная с которого выполняется условие . Обозначим черезМ наибольшее из следующих чисел . Очевидно, чтодля любого номераn, а это и означает, что последовательность {} – ограничена.

Теорема 4. Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.

Доказательство. Пусть – ограниченная, а– бесконечно малая последовательности. Это означает, что существует числоМ>0 такое, что для любого номера n выполняется , и для любого числасуществует номерN такой, что для всех номеров выполняется. Тогда для всех номеров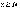и любогоε>0 выполняется 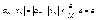, а это и означает, что последовательность– бесконечно малая.

Следствие. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Теорема 5. Если элементы бесконечно малой последовательности равны одному и тому же числуС, то С=0.

Доказательство. Предположим, что . Длясуществует такой номерN, что для всех номеров выполняется. Так как, а, то последнее неравенство имеет вид, откуда. Полученное противоречие показывает, что предположениеневерно, следовательно,.

Теорема 6. Если – бесконечно большая последовательность то, начиная с некоторого номера n, определена последовательность, которая является бесконечно малой. Если не все элементы бесконечно малой последовательностиравны нулю, то последовательностьбесконечно большая.

Доказательство. Пусть– бесконечно большая последовательность. Это означает, что для любого положительного числаМ можно указать такой номер N, что для всех номеров выполняется. А это означает, что привсе элементы, а поэтому последовательностьимеет смысл с номераN. Пусть - любое положительное число. Для числаможно указать номер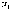такой, что дляnNвыполняется . Это и означает, что– бесконечно малая. Доказательство второй части теоремы проводится аналогично.

Рассмотрим теперь лемму, которая будет использоваться при доказательстве некоторых теорем.

Лемма. Для того чтобы число а являлось пределом последовательности , необходимо и достаточно, чтобыимел вид,n=1,2,…, где есть бесконечно малая последовательность.

Доказательство. Обозначим . Условиепо определению предела равносильно тому, что для любого числасуществует такой номерN, что для всех номеров выполняется неравенство, то есть, а это и равносильно тому, что.

Эта лемма показывает особую роль бесконечно малых последовательностей при изучении предела последовательности. Перейдем теперь непосредственно к рассмотрению простейших свойств пределов числовых последовательностей.

ВОПРОС№5. Непрерывность функции в точке. Точки разрыва. Классификация точек разрыва.

1) Пусть функция f(x) определена в некоторой окрестности O(x₀) точки x₀ (включая саму точку x₀).

Функция f(x) называется непрерывной в точке x₀, если существует lim_x → x0 f(x) , равный значению функции f(x) в этой точке:

lim x → x0  f(x) = f(x0),

(1)

т.е.

 O( f(x0) )      O(x0) :     x  O(x0)  f(x)  O( f(x0) ) .

Замечание. Равенство (1) можно записать в виде:

lim x → x0  f(x) = f ( lim x → x0  x ),

т.е. под знаком непрерывной функции можно переходить к пределу.

Пусть Δx = x − x₀ — приращение аргумента, Δy = f(x) − f(x₀ ) — соответствующее приращение функции.

Необходимое и достаточное условие непрерывности функции в точке

Функция y = f(x) непрерывна в точке х₀ тогда и только тогда, когда

lim Δx → 0  Δy = 0.

(2)

Замечание. Условие (2) можно трактовать как второе определение непрерывности функции в точке. Оба определения эквивалентны.

Пусть функция f(x) определена в полуинтервале [x₀, x₀ + δ ).

Функция f(x) называется непрерывной справа в точке x₀, если существует односторонний предел

lim x → x0 + 0  f(x) = f(x0).

Пусть функция f(x) определена в полуинтервале (x₀ − δ, x₀].

Функция f(x) называется непрерывной слева в точке x₀, если существует односторонний предел

lim x → x0 − 0  f(x) = f(x0).

2) Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.

Непрерывна при x = a.		Имеет разрыв при x = a.
Непрерывна при x = a.		Имеет разрыв при x = a.
Рисунок 1.