ФИЗИЧЕСКАЯ ХИМИЯ Учебное пособие для студентов заочной формы обучения инженерных специальностей

К таким свойствам относятся: понижение температуры замерзания ( Tзам), повышение температуры кипения ( Tкип), осмотическое давление ( = CRT), относительное понижение давления насыщенного пара.

На рисунке 3.1.1 показано, как изменяются температуры замерзания и кипения воды по сравнению с её раствором.

Рис. 3.1.1

Различие между температурами замерзания и кипения «чистой» воды и водного раствора (кривые плавления и испарения для раствора показаны пунктиром, а для воды сплошной линией)

Изотонический коэффициент Вант-Гоффа

Исследования показали, что закономерности, представленные на рисунке, характерны только для очень разбавленных растворов неэлектролитов.

В растворах кислот, щелочей и большинства солей (электролитов) эти соотношения не выполняются. Наблюдаемые при этом величины Tзам и Tкип, а также осмотического давления несколько выше, чем теоретически рассчитанные по приведенным формулам. Вант-Гофф5 предложил ввести в

указанные соотношения эмпирический коэффициент ( i ), названный впоследствии изотоническим коэффициентом Вант-Гоффа.

С учетом изотонического коэффициента ( i ) связь между величинами

изменений температур (см.рис.3.1.1) замерзания ( Tзам = To,зам - Tзам) и кипения ( Tкип = Tкип - To,кип), осмотического давления ( ) и концентрацией раствора записывается в следующем виде:

5 ВАНТ-ГОФФ Якоб Хендрик (1852-1911) - нидерландский физикохимик первый лауреат Нобелевской премии по химии (1901).

181

где C - молярная (моль/л), а m - моляльная (моль/кг растворителя) концентрации. Коэффициент i > 1 и по мере разбавления растворов электролитов стремится к целому числу ( i = 2, 3, 4 ).

Физический смысл изотонического коэффициента Вант-Гоффа стал ясен после появления теории электролитической диссоциации, созданной шведским физикохимиком Аррениусом в 1887 году. В соответствии с этой теорией, вследствие взаимодействия молекул растворителя и растворенного вещества, последние распадаются (диссоциируют) на ионы. Диссоциация приводит к увеличению общего числа частиц в растворе в i раз и, следовательно, к увеличению коллигативных свойств.

Изотонический коэффициент равен отношению числа частиц ( ), образовавшихся в растворе после растворения ( о) молекул i = / о. Исходя из величины изотонического коэффициента Вант-Гоффа можно определить величину степени диссоциации растворенного вещества:

= [ о + о (1 - ) ]

i = [ о + о (1 - ) ] / о = + (1 - ) = ( - 1) + 1)

где - число ионов, образующихся при распаде каждой диссоциирующей молекулы растворенного вещества. Величина степени диссоциации электролита изменяется в пределах от нуля до единицы:

0 ( = дисс / раств ) 1 .

Сильные электролиты в водных растворах полностью распадаются на ионы и для них степень диссоциации равна единице ( = 1), а в случае слабых электролитов степень диссоциации меньше единицы ( < 1).

У сильных электролитов изотонический коэффициент должен быть равен числу ионов, на которые распадается молекула ( i = ), но оказалось, что и для растворов сильных электролитов это равенство не выполняется ( i ), хотя величина i стремится к по мере разбавления раствора. Для учета несоответствий между теоретическими и экспериментальными значениями величин Tзам, Tкип и применяется осмотический коэффициент ( ):

при бесконечном разбавлении (m 0) величина осмотического коэффициента стремится к единице ( 1), а Tзам Kзам m.

182

Сильные и слабые электролиты

Электролиты (вещества с ионной природой электрической проводимости) называют также проводниками второго рода. Перенос электричества в таких веществах осуществляется за счет миграции в электрическом поле ионов двух типов: катионов Ktz+, имеющих заряд z+ и анионов Anz- с зарядом z-.

Появление ионов в растворе происходит в результате электролитической диссоциации, а также при разрушении ионной кристаллической решетки в процессе растворения.

Электролиты можно условно разделить на два вида – ионогенные и ионофорные электролиты.

Ионогенные электролиты в “чистом виде” (вне раствора) не содержат ионов, появление ионов в растворах ионогенных электролитов происходит в результате распада (диссоциации) молекул. Например, при растворении хлороводорода в воде молекулы HCl распадаются (диссоциируют) и в результате образуются катионы водорода H+ и анионы хлора Cl .

Ионофорные электролиты и в исходном виде (например, в твердом состоянии) и до растворения в своей структуре содержат ионы. Так, в кристаллической решетке хлорида натрия располагаются катионы Na+ и анионы Cl , а в процессе растворения кристаллов хлорида натрия эти ионы переходят в жидкую фазу (в раствор).

Электролитическая диссоциация

Распад молекул электролита на ионы называется электролитической диссоциацией, классическая теория этого процесса была создана Аррениусом19. Электролитическую диссоциацию электролитов описывают при помощи уравнений вида:

В уравнениях вида (1), знак равенства используется в тех случаях, когда все исходные частицы (молекулы) вида Kt An содержащие число катионов Ktz+ и - анионов Anz-, полностью диссоциированы, т.е. в растворе имеются только ионы.

Электролиты, диссоциация которых описывается химическими уравнениями вида (3.1.9а), называются сильными.

В том случае, если диссоциации подвержена лишь часть растворенных частиц (молекул), уравнение (3.1.9а) записывают в виде:

19 АРРЕНИУС Сванте Август (19.II.1859 – 2.X.1927) - шведский ученый физикохимик, один из основоположников физической химии. Нобелевская премия в 1903 г.

183

а электролит называют - слабым.

При равенстве скоростей прямого (диссоциации) и обратного (моляризации) процессов в растворе слабого электролита устанавливается равновесие между концентрациями продуктов распада (ионов) и недиссоциированных молекул. При этом в целом для раствора всегда выполняется правило электронейтральности, согласно которому суммарный заряд катионов равен суммарному заряду анионов:

где дисс - число молекул слабого электролита, распавшихся на ионы из общего числа раств растворенных. Степень диссоциации выражают либо в долях единицы или в процентах, для чего значение , рассчитанное по формуле (3.1.10) домножают на 100%.

Степень диссоциации зависит от природы электролита и растворителя, температуры и концентрации электролита:

природа, T, C

Таблица 3.1.3

Диэлектрическая проницаемость20 некоторых жидкостей

при температуре 25 С

Диссоциации подвергаются только те вещества, в молекулах которых имеются полярные и ионные связи, и только при растворении в полярных растворителях. При этом в наибольшей мере диссоциация протекает в

20 относительная

184

растворителях (см.таблицу 3.1.3) с высокой диэлектрической проницаемостью

( ).

Распад молекул на ионы происходит за счет энергии электростатического взаимодействия между полярными молекулами растворенного вещества и растворителя. Образовавшиеся в результате диссоциации ионы окружаются молекулами воды (полярного растворителя). Явление, заключающееся во взаимодействии ионов с молекулами полярного растворителя (воды) называется сольватацией (гидратацией) иона. В результате гидратации (сольватации) вокруг иона образуется гидратная (сольватная) оболочка.

Гидратация (сольватация) является экзотермическим процессом. Тепловой эффект, сопровождающий гидратацию ионов, называемый теплотой гидратации, по своей величине сравним с тепловыми эффектами химических реакций.

Гидратация (сольватация) ионов препятствует обратному соединению ионов в молекулы. Образование гидратных (сольватных) оболочек уменьшает электростатическое взаимодействие между ионами в растворе, которое существенно зависит от диэлектрической проницаемости.

Сильные электролиты в растворе существуют в виде сольватированных (в водном растворе - гидратированных) ионов.

К сильным электролитам относятся: сильные кислоты, например: HCl, HBr, HI, H2SO4 , HMnO4 , HNO3 , HClO4 , HClO3; HBrO4 , HBrO3 , HIO4 , HIO3 ; сильные основания (гидроксиды щелочных и щелочно-земельных металлов); почти все соли.

В растворах слабых электролитов одновременно сосуществуют и недиссоциированные молекулы и сольватированные (в водных растворах - гидратированные) ионы.

К слабым электролитам относятся: слабые кислоты, например: HCN,

H3BO3, HF, H2SO3, H2CO3, HNO2, HClO2, HClO, CH3COOH, H3PO4 , H2S,

большинство органических кислот - CH3COOH, HCOOH и др.; слабые основания - все (кроме, гидроксидов щелочных и щелочноземельных металлов); некоторые соли - например, HgCl2 , Hg(CN)2 , CdI2 и вода.

Равновесия в водных растворах слабых электролитов

В растворах слабых электролитов устанавливается равновесие между продуктами диссоциации - ионами и недиссоциировавшими молекулами. Например, в растворе синильной кислоты HCN это равновесие можно

представить в виде:

HCN  H+ + CN-

Состояние подвижного химического равновесия характеризуется равенством скоростей прямой и обратной реакций. Количественно соотношение равновесных концентраций продуктов ионного распада и

185

недиссоциированных молекул характеризуется величиной константы равновесия :

Значения константы диссоциации определяется исходя из термодинамических свойств веществ и приводятся в справочниках. На основании величин констант диссоциации и концентрации слабого электролита в растворе можно рассчитать равновесные концентрации ионов водорода [H+], цианид-ионов [CN-] и недиссоциированных молекул кислоты

[HCN].

Для расчетов используется величина степени диссоциации

= Nдисс / Nраств = дисс/ раств = Cдисс / C ,

где Nдисс , дисс и Cдисс - соответственно, число, количество вещества и концентрация диссоциировавших (распавшихся) на ионы молекул электролита, а Nраств, раств и C - число растворенных молекул, количество вещества и концентрация электролита в растворе. Тогда, равновесная концентрация недиссоциированных молекул в растворе кислоты равна

[HCN] = С – C = С (1 – ),

Равновесные концентрации ионов водорода и цианид-ионов согласно уравнению электролитической диссоциации равны

[H+] = [CN-] = C.

Тогда, подставив в выражение для константы равновесия величины равновесных концентраций, выраженные через степень диссоциации и общую концентрацию электролита, получим

а после упрощения придём к выражению, называемому законом разбавления Оствальда:

Если степень диссоциации электролита намного меньше единицы <<1, то закон разбавления (разведения) Оствальда можно представить в виде:

Отсюда степень диссоциации :

186

Как видно, при уменьшении концентрации раствора степень диссоциации электролита растёт, достигая значения = 1 при бесконечном разбавлении (C 0). Следовательно, в бесконечно разбавленном растворе стирается различие между понятиями сильный и слабый электролит.

Если > 0.01, то для определения степени диссоциации выражение для закона разбавления преобразуют к виду:

Решив это квадратное уравнение, выбираем корень, удовлетворяющий условию

0 < < 1.

РАСТВОРЫ СИЛЬНЫХ ЭЛЕКТРОЛИТОВ

ПОНЯТИЕ ОБ АКТИВНОСТИ. КОЭФФИЦИЕНТ АКТИВНОСТИ

Сильные электролиты при растворении в воде полностью распадаются на ионы. Поскольку концентрация недиссоциированных молекул в этом случае практически равна нулю, то выражение для константы диссоциации вида (3.1.11) для сильных электролитов теряет смысл. Вследствие относительно высокой концентрации ионов взаимодействие между ними, а также полярными молекулами воды, оказывает существенное влияние на свойства даже очень разбавленных растворов сильных электролитов. С ростом концентрации электролита расстояние между ионами в растворе уменьшается. Усиливающиеся при этом ион-ионное и ион-дипольное взаимодействия как между самими ионами, так и между ионами и гидратными оболочками при достаточном сближении ионов могут приводить к образованию ионных пар, или, в общем случае, ионных ассоциатов. В отличие от молекул, ионы в таких ассоциатах непосредственно друг с другом не соприкасаются, так как разделены одним или даже несколькими слоями гидратных оболочек.

Образование ионных ассоциатов при экспериментальном исследовании свойств растворов сильных электролитов создает лишь иллюзию неполной диссоциации. Поэтому понятие "степень диссоциации" для растворов сильных электролитов носит условный характер и должно использоваться с добавлением слова "кажущаяся".

Сильное взаимодействие между ионами, а также ионами и дипольными молекулами воды приводит к тому, что свойства растворов, особенно зависящие от числа (концентрации) и подвижности ионов, для сильных электролитов проявляются существенно иначе, чем для слабых, где межионным взаимодействием можно пренебречь.

187

Теоретическое описание свойств растворов сводится к составлению уравнений, связывающих определенное свойство раствора с его концентрацией. Такие уравнения строго получены для растворов, в которых отсутствуют межионные взаимодействия. Понятно, что на самом деле таких растворов нет, поэтому их называют идеальными (существующими лишь как идея). Т.е. любое свойство идеального раствора электролита (плотность, вязкость, электропроводность и т.д.) выражается в теоретических уравнениях как функция концентрации. Попытки использовать эти уравнения для описания свойств реальных (неидеальных) растворов показали отличие вычисленных и экспериментально измеренных свойств.

Для расчетов свойств реальных растворов электролитов Г.Н.Льюисом был предложен следующий путь. Сохраняется вид уравнения, используемый для идеальных растворов, но вместо концентрации подставляется такая специально придуманная величина, которая делает результат расчета совпадающим с экспериментально найденным значением. Эту величину назвали активностью электролита в растворе. Так, если в 0.1 М растворе хлороводородной кислоты активности ионов Н+ и Cl- равны 0.08, то это означает, что данные ионы действуют в химических реакциях (влияют на свойства) так, как если бы их концентрации составляли не 0.1, а 0.08 .

Для сильного электролита, диссоциирующего по схеме (3.1.9а) общая активность электролита равна произведению активностей отдельных ионов

где + и - - число катионов и анионов, образующихся при распаде одной молекулы электролита.

Определить раздельно активности катионов и анионов не представляется возможным, так как невозможно приготовить раствор , содержащий только один вид ионов. Поэтому вместо них используют среднеионную активность электролита

где = + + -

Для определения общей активности раствора электролита используются различные экспериментальные методы.

Наиболее часто активность выражается с помощью моляльной шкалы концентраций. В этом случае активность связана с концентрацией

моляльность и коэффициент активности раствора электролита соответственно.

188

Среднеионная моляльность (m ) выражается через моляльную концентрацию раствора электролита (m) формулой

Таблица 3.1.4. Значения фактора валентности s и формулы для расчета среднеионной активности а± электролитов разного типа

Как видно из (3.1.17), коэффициент активности формально учитывает влияние межионного взаимодействия на свойства раствора электролита.

189

Величины коэффициентов активности существенно зависят от природы веществ, составляющих раствор, зарядов и концентрации ионов, температуры и изменяются в широких пределах.

Влияние одновременного присутствия в растворе нескольких различных ионов на активность каждого из них Льюис предложил количественно характеризовать с помощью ионной силы раствора ( I ), которая принимается равной полусумме произведений концентраций21 на квадрат заряда всех ионов, присутствующих в растворе:

Для 1,1-валентного электролита молярные концентрации катионов и анионов одинаковы и равны его молярной концентрации

C+ = C- = C , поэтому I = ½ [C 12 + C (-1)2 ] = C

В соответствии с первым приближением теории Дебая – Хюккеля взаимосвязь активности иона и ионной силы раствора имеет вид

Соотношение служит для определения коэффициента активности отдельного иона, который нельзя измерить экспериментально, поэтому на практике используется среднеионный коэффициент активности

f н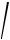 f f

21Состав раствора может выражаться величинами моляльной (m) или молярной (С) концентрации, а также в мольных долях (Х).

22Дамаскин Б.Б., Петрий О.А., Цирлина Г.А. Электрохимия : Учебник для вузов. – М.:

Химия. 2001. – 624 с.: ил.

190