
ФИЗИЧЕСКАЯ ХИМИЯ Учебное пособие для студентов заочной формы обучения инженерных специальностей
.pdf
число компонентов равно
k 3 2 1 |
|
|
так как число уравнений равно 2: |
|
|
K P PHCl PNH 3 |
и |
PHCl PNH3 |
Термодинамические степени свободы. Параметры, определяющие состояние системы, которые можно менять произвольно и независимо один от другого, не вызывая при этом изменения числа или природы фаз в системе (фазового состава системы) называются термодинамическими степенями свободы. В качестве таких параметров, как правило, выбирают давление, температуру и концентрации (содержание) компонентов. Кроме того, в роли термодинамических степеней свободы могут выступать параметры, характеризующие интенсивность электрического и магнитного полей, а также поверхностное натяжение и др.
Число термодинамических степеней свободы, условно обозначаемое строчной латинской буквой s и часто называемое вариантностью системы, в состоянии равновесия связано с числом компонентов k и числом фаз f, уравнением, которое получило особое название – правило фаз Гиббса.
ПРАВИЛО ФАЗ ГИББСА
Правило фаз, выведенное Гиббсом9 в 1875-1878 годах, называют также основным законом фазовых равновесий. Этот закон устанавливает взаимосвязь между числом компонентов k, числом фаз f и вариантностью s равновесной термодинамической системы10 и выражается уравнением
s = k – f + n, |
(2.1.1) |
где n – общее число переменных величин, характеризующих состояние системы. Если кроме концентраций параметрами, определяющими состояние системы, являются только давление и температура, то n = 2, а правило фаз Гиббса принимает вид
s = k – f + 2. |
(2.1.1а) |
В частных случаях, когда в системе один из параметров поддерживается неизменным, например, давление или температура (т.е. в изобарных или изотермических условиях), определяют условную вариантность системы
sусл. = k – f + 1 |
(2.1.1б) |
9ГИББС Джозайя Уиллард (11.02.1839 – 28.04.1903) – американский ученый физик и физико-химик, один из основоположников термодинамики.
10Правило фаз неприменимо к системам, в которых фазы разделены полупроницаемыми перегородками.
121

или |
дважды |
условную |
вариантность, |
например, |
в |
случае |
изобарно-изотермических условий, когда и P=const и T=const) |
|
|
||||
|
|
sусл.(2) = k – f . |
|
(2.1.1в) |
||
Если в равновесной системе число термодинамических степеней свободы s = 2, то она называется бивариантной, это означает, что произвольным образом и независимо друг от друга не вызывая изменения фазового состава системы (числа фаз) можно произвольно менять 2 параметра состояния.
Когда s = 1, система называется моновариантной и произвольным образом может изменяться только один параметр.
При s = 0 ни один из параметров состояния не может изменяться, не вызывая изменения фазового состава. В этом случае систему называют
безвариантной или нонвариантной.
УСЛОВИЕ ТЕРМОДИНАМИЧЕСКОГО РАВНОВЕСИЯ В ГЕТЕРОГЕННОЙ СИСТЕМЕ
Для открытой системы при P = const и T = const условием равновесия является выполнение равенств (1.II. 38б) и (1.II.51). Если в равновесии находятся две фазы
|
n |
|
|
1 |
(2.1.2) |
||
ФАЗА(1) ФАЗА(2) |
|||
|
n2 |
|
|
то выражение (1.II.51) примет вид: |
|
||
- n1 м1 n2 м2 0 |
|
||
|
|
|
|
|
м1 м2 |
|
(2.1.3) |
поскольку n1 n2 .
В многофазной гетерогенной системе условием равновесия является равенство химических потенциалов для каждого i-го компонента во всех f фазах:
м1i мi2 м3i |
мi4 мif |
(2.1.4) |
|
|
|
ФАЗОВЫЕ РАВНОВЕСИЯ В ОДНОКОМПОНЕНТНЫХ СИСТЕМАХ
В однокомпонентной системе, состояние которой определяется двумя параметрами - давлением и температурой - в равновесии число фаз не может
122

быть более fmax. Подсчитаем это число с помощью правила фаз Гиббса при k = 1 :
s = k - f + 2 = 1 - f + 2 = 3 - f
откуда |
|
f = 3 - s |
(2.1.5) |
максимальное число фаз получим |
при s = 0, следовательно |
|
fmax = 3 - s = 3 |
- 0 = 3. |
(2.1.6) |
УРАВНЕНИЕ КЛАПЕЙРОНА-КЛАУЗИУСА
Для двухфазной гетерогенной системы условием равновесия между двумя фазами
ФАЗА(1) |
|
ФАЗА(2) |
|
|
(2.1.7) |
является равенство химических потенциалов
1 = 2 .
В случае индивидуального вещества при n = 1 моль химический потенциал равен энергии Гиббса G. Поэтому равенство химических потенциалов можно заменить равенством энергий Гиббса
dG1 = dG2 .
Согласно объединённому |
|
выражению первого |
|||||||
термодинамики |
|
|
|
|
|
|
|
|
|
|
|
dG1 |
|
= V1 dP - S1 dT |
|||||
тогда |
dG2 |
= V2 dP - S2 dT , |
|||||||
V1 dP - S1 dT = V2 dP - S2 dT , |
|||||||||
откуда |
|||||||||
|
|
|
|
|
|
|
|
||
или |
(V1 - V2) dP = (S1 - S2) dT |
||||||||
|
|
|
|
|
|
|
|
||
dP |
|
S |
|
S |
2 |
|
ДSф.п. |
||
|
|
1 |
|
ДVф.п. |
|||||
dT равн. |
|
V1 V2 |
|
||||||
ивторого начал
(2.1.8)
В общем виде изменение энтропии при фазовом превращении равно
S |
ф.п. |
|
Hф.п. |
(2.1.9) |
|
|
T |
|
|
|
|
|
ф.п. |
|
где Hф.п. и Tф.п. - теплота и температура фазового превращения. Произведём замену и тогда окончательно для (2.1.8) получим
123

dP |
|
ДHф.п. |
|
|
|
|
Tф.п. ДVф.п. |
(2.1.10) |
|
dT |
равн. |
|
||
Выражение (2.1.10) называется уравнением Клапейрона-Клаузиуса в
дифференциальной форме. Оно является универсальным уравнением, применимым к любому двухфазному равновесию.
ПРИМЕНЕНИЕ УРАВНЕНИЯ КЛАПЕЙРОНА-КЛАУЗИУСА ДЛЯ РАССМОТРЕНИЯ ФАЗОВЫХ ПРЕВРАЩЕНИЙ
Плавление
Рассмотрим равновесие между твёрдой и жидкой фазами
плавление |
|
|
|
ЖИДКАЯ ФАЗА |
(2.1.11) |
ТВЁРДАЯ ФАЗА |
||
кристаллизация |
|
|
В этом случае уравнение Клапейрона-Клаузиуса используют для анализа влияния давления на температуру плавления, поэтому выражение (2.1.10) записывают в виде
dT |
|
T |
ДV |
(2.1.12) |
|
|
|
пл. |
пл. |
||
dP равн. |
|
ДHпл. |
|
||
где Tпл.- температура плавления, ДHпл.- теплота плавления, ДVпл. - изменение объёма системы при плавлении.
Характер изменения температуры плавления определяется знаком производной в выражении (2.1.12). Поскольку Tпл.> 0 и ДHпл. > 0, то знак
производной будет определяться знаком величины ДVпл. .
Для большинства веществ объём при плавлении увеличивается ДVпл. > 0 и, следовательно,
dT |
0 |
|
|
|
|
(2.1.13) |
|
dP |
равн. |
|
|
поэтому с ростом давления температура плавления таких веществ увеличивается.
Однако имеется небольшое число веществ (вода, висмут, галлий, серый чугун) для которых наблюдается иная (аномальная) зависимость. У этих веществ при плавлении происходит уменьшение объёма ДVпл. < 0, производная
124

dT |
|
0 |
|
|
|
|
|
(2.1.14) |
|
dP |
равн. |
|
||
|
|
|||
меньше нуля и увеличение давления приводит к снижению температуры плавления.
Испарение и возгонка (сублимация)
Рассмотрим равновесие между жидкой и газовой фазами
испарение
ЖИДКАЯ ФАЗА ГАЗ (ПАР) (2.1.15)
конденсация
Изменение объёма при испарении представляет собой разность между объёмом пара и жидкости
Vисп = Vпар – Vж
Сравним объёмы одного и того же количества вещества в жидкой и паровой фазах. Объём в паровой фазе при температуре кипения и стандартном давлении можно оценить исходя из уравнения Клапейрона-Менделеева
PV нRT .
Пусть имеется вода в количестве = 1 моль, тогда
Vпар = ν R T / P = 1∙8,31∙ 373 / 101320 = 0,0306 м3 = 30 600 см3
Плотность жидкой воды при температуре 100 С и атмосферном давлении равна = 0.958 г/см3. Тогда объём жидкой воды для тех же условий будет равен
Vж |
н(H2O) M (H 2O) |
|
1 |
18 |
18.8 |
см |
3 |
с |
0.958 |
|
|||||
|
|
|
|
|
|||
Как видно в одинаковых условиях объём паровой фазы во много раз
больше, чем объём жидкой |
Vпар Vж, поэтому можно считать, что |
|||||||||||
|
|
Vисп. Vпар Vж Vпар RT / P . |
|
|||||||||
С учетом сказанного уравнение (2.1.10) примет вид |
|
|
||||||||||
dP |
|
|
ДH |
исп. |
|
ДH |
исп. |
ДH |
исп. |
|||
|
|
|
|
|
|
|
||||||
dT |
равн. |
|
T |
|
|
ДV |
|
T |
V |
T ( RT / P) |
||
|
|
|
кип. |
|
|
кип. |
пар |
|
|
|||
125
dP |
|
ДH |
исп. |
P |
|
|
|
|
(2.1.16) |
||
dT равн. |
|
R T2 |
|||
Разделим переменные в уравнении (2.1.16) и проинтегрируем его
P |
|
R T2 |
|
|
dP |
|
ДHисп. |
dT , |
(2.1.17) |
|
|
ПРИ ТЕМПЕРАТУРАХ ДАЛЁКИХ ОТ КРИТИЧЕСКОЙ МОЖНО СЧИТАТЬ, ЧТО
ДHисп. f (T )
теплота испарения не является функцией температуры. Вынесем постоянные величины в правой части (2.1.17) за знак интеграла
dP ДHисп. dT P R T2
и тогда после интегрирования получим следующее выражение
ln P |
ДHисп. const , |
(2.1.19) |
|
RT |
|
которое представляет собой уравнение Клапейрона-Клаузиуса в интегральной форме. Оно описывает зависимость давления насыщенного пара над жидкостью от температуры. Это выражение часто представляют в виде
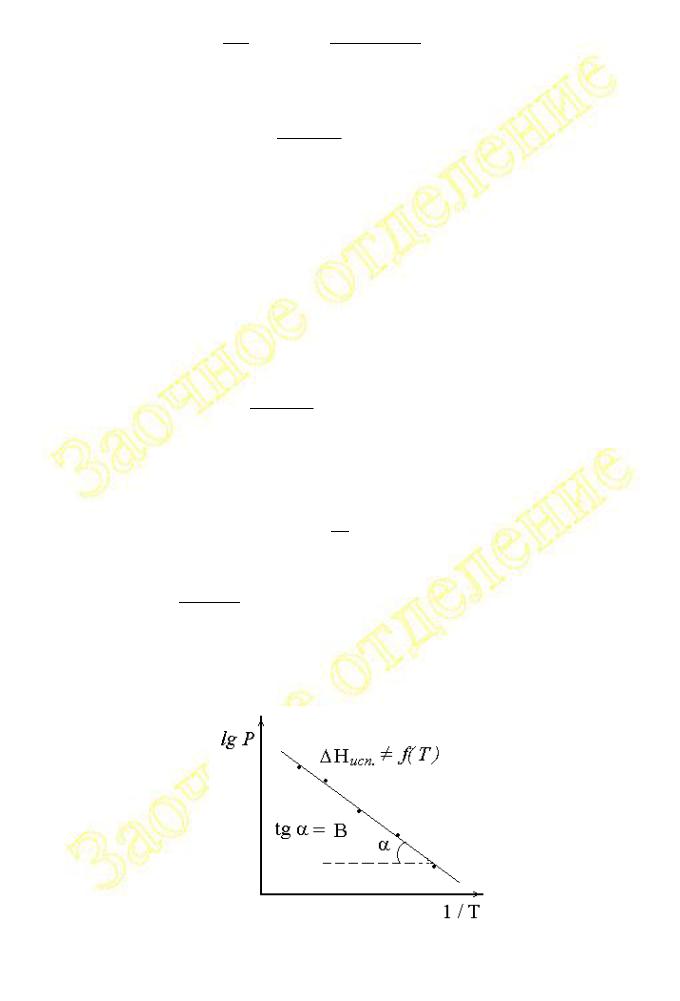
lg P A |
B |
, |
(2.1.20) |
|
T |
|
|
где коэффициент A равен постоянной интегрирования A = const, а другой
коэффициент B ДHисп. .
2.303 R
Из выражения (2.1.19) следует, что при ДHисп. f (T ) график зависимости lg P f (1/T) имеет линейный характер (см. рис.2.1.1).
Рис.2.1.1
126
Для равновесия
возгонка ТВЁРДАЯ ФАЗА ГАЗ (2.1.21)
конденсация
интегральная форма уравнения Клапейрона - Клаузиуса имеет аналогичный вид
ln P |
ДHвозг. |
const |
(2.1.22) |
|
RT |
|
|
и может быть представлена линейной функцией вида (2.1.20). Зависимости (2.1.20) и (2.1.22) отличаются только коэффициентами A и B.
Следует иметь в виду, что коэффициенты A и B не вполне постоянны, поскольку условие (2.1.18) является лишь приближённым.
ПРИМЕР АНАЛИЗА ДИАГРАММЫ СОСТОЯНИЯ ОДНОКОМПОНЕНТНОЙ СИСТЕМЫ
Диаграмма состояния воды
Соотношения (2.1.12), (2.1.20) и (2.1.22), вытекающие из уравнения Клапейрона - Клаузиуса, можно представить графически в виде диаграммы состояния.
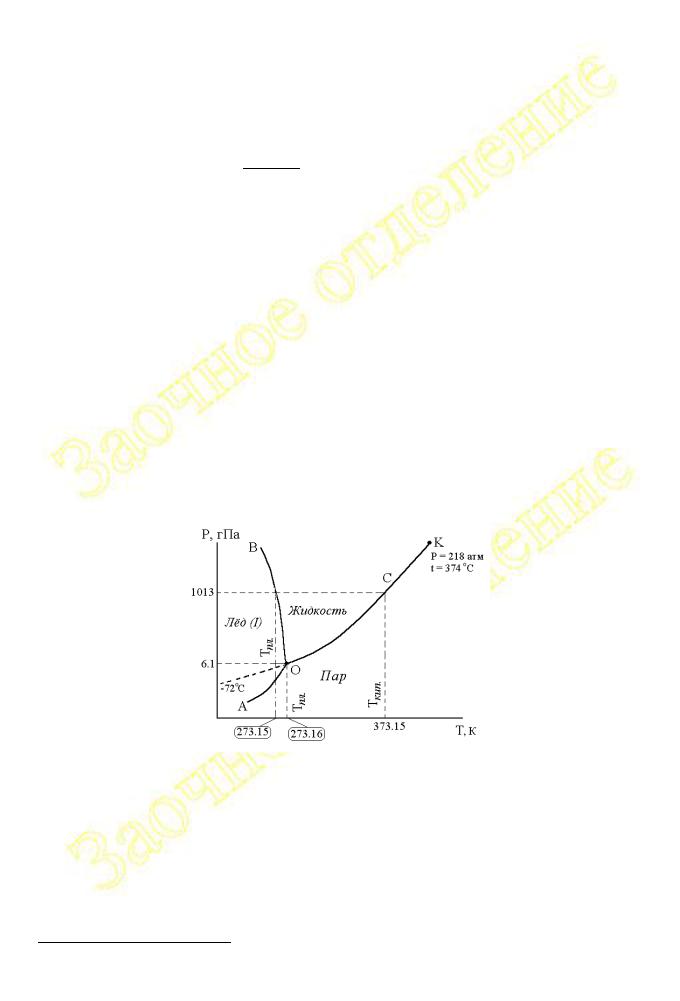
На рис.2.1.2 в качестве примера такой диаграммы приведена фазовая диаграмма состояния воды в координатах давление - температура.
Рис.2.1.2 Диаграмма состояния воды в области невысоких давлений11
На диаграмме состояния воды условно (без соблюдения масштаба) изображены линии, описывающие следующие экспериментально полученные зависимости: AO - зависимость давления насыщенного пара над твёрдой фазой (льдом) от температуры (кривая возгонки), OB - зависимость температуры
11 приведена схематично без соблюдения масштаба
127

плавления льда от давления (кривая плавления), OK - зависимость давления насыщенного пара над жидкой водой от температуры (кривая испарения).
Все три линии пересекаются в точке O, называемой тройной точкой. Тройная точка отвечает состоянию системы, в котором в равновесии находятся три фазы: жидкая вода, лёд и пар.
Каждая из трёх линий отвечает равновесию каких-либо двух фаз: линия OB описывает условия сосуществования твёрдой и жидкой фаз, согласно равновесию (2.1.11); линия AO — твёрдой и газовой фаз, согласно равновесию (2.1.21); линия OK — жидкой воды и пара, согласно равновесию (2.1.15). В любой точке, лежащей на этих линиях* и описывающей условия равновесия между двумя фазами, термодинамическая вариантность системы будет равна
s = k - f + 2 = 1 - 2 + 2 = 1.
Кривая испарения OK обрывается в точке K, называемой критической точкой. При температурах, превышающих температуру критической точки, исчезает всякое различие между жидкостью и паром. В состоянии, которому соответствует тройная точка, число степеней свободы у системы равно
s = k - f + 2 = 1 - 3 + 2 = 0.
Кривые плавления, возгонки и испарения делят поле диаграммы на три области, каждая из которых характеризует условия существования одной из фаз: область AOB - льда; область BOK - жидкой воды; AOK - пара. Точки на диаграмме, лежащие на указанных областях (но не на линиях), отвечают состояниям системы с вариантностью равной
s = k - f + 2 = 1 - 1 + 2 = 2.
Наклон линии OB относительно перпендикуляра, проведённого к оси температур, отражает одну из многочисленных аномалий воды, выражаемую неравенством (2.1.14).
Пунктирная линия на диаграмме показывает возможность существования жидкой воды в переохлаждённом (метастабильном) состоянии при температурах на много градусов ниже температуры её замерзания. В литературе имеются сведения о возможности понижения температуры жидкой воды без кристаллизации вплоть до -72 С.
МЕТОД ФИЗИКО-ХИМИЧЕСКОГО АНАЛИЗА
Метод физико-химического анализа (далее МФХА) применяется для изучения сложных (многокомпонентных) систем в тех случаях, когда трудно
* за исключением точки O !
128

установить точные аналитические зависимости между различными параметрами состояния и свойствами системы.
Начало развитию МФХА положено в работах Д.И.Менделеева*, Г.Г.И.А.Таммана**, А.Л. Ле Шателье***. Огромное значение для становления МФХА сыграли работы Николая Семеновича Курнакова*.
МФХА основан на экспериментальном изучении зависимостей вида
СВОЙСТВО = f(состава; T, P и др.),
свойства равновесной физико-химической системы как функции состава и условий существования (факторов определяющих состояние равновесия).
Диаграммы состояния
Основным приемом МФХА является построение диаграмм состояния. В рамках этого метода зависимости свойств системы от её состава и внешних условий (P, T) изображают графически в виде диаграмм "состав - свойство".
Состав на диаграммах обычно откладывают по оси абсцисс, а свойство по оси ординат. В зависимости от состава графически представляют многие свойства такие, например, как электрическая проводимость, теплопроводность, твёрдость, вязкость, температура фазовых превращений и др.
Изучение диаграмм состояния позволяет выяснить характер взаимодействия компонентов системы, а также судить о химическом составе и границах существования фаз.
Построение и анализ диаграмм состояния базируется на двух принципах – соответствия и непрерывности, которые формулируются следующим образом.
1. Принцип соответствия. |
Каждому сочетанию фаз, находящихся в |
|||
равновесии в |
данной системе, |
на диаграмме |
состояния |
отвечает |
(соответствует) |
определенный |
геометрический |
образ (точка, |
линия, |
поверхность и т.д.).
2. Принцип непрерывности. При непрерывном изменении параметров, определяющих состояние системы (P,T, концентрация), свойства её отдельных фаз и системы в целом изменяются также непрерывно до тех пор, пока не изменится число или характер фаз (фазовый состав). При появлении
*МЕНДЕЛЕЕВ Дмитрий Иванович (1834 – 1907) великий русский ученый-химик, в 1863 – 1872 гг. профессор Петербургского технологического института.
**ТАММАН Густав Генрих Иоганн Аполлон (1861 – 1938) немецкий физикохимик. Применил термический анализ для изучения металлических сплавов, заложив основы современной металлографии.
***ЛЕ ШАТЕЛЬЕ Анри Луи (1850 – 1936) французский физикохимик и металловед.
*КУРНАКОВ Николай Семенович (1860 – 1941) советский химик, академик. Основатель и директор (1918 – 1934) Института физико-химического анализа АН СССР.
129
новых или исчезновении существующих фаз свойства системы изменяются скачкообразно, на зависимостях "состав - свойство" появляются изломы, горизонтальные участки и др. нарушения непрерывности.
Физико-химический анализ является наиболее общим методом исследования превращений веществ. Он широко применяется в металлургии, технологии силикатов, минералогии и других областях.
ТЕРМИЧЕСКИЙ АНАЛИЗ
Термический анализ является частным случаем физико-химического анализа и представляет собой совокупность экспериментальных методов определения температуры, при которой в равновесной системе происходит изменение фазового состава (числа фаз).
В рамках термического анализа объектом изучения являются диаграммы состояния, построенные в координатах “температура фазового превращения - состав системы”. Частным случаем таких диаграмм являются диаграммы плавкости. Диаграммы плавкости строят в координатах “температура плавления - состав” или “температура кристаллизации - состав”.
Первичные данные для построения таких диаграмм получают при изучении закономерностей изменения температуры системы определённого состава во времени при медленном (с постоянной скоростью) нагревании или охлаждении.
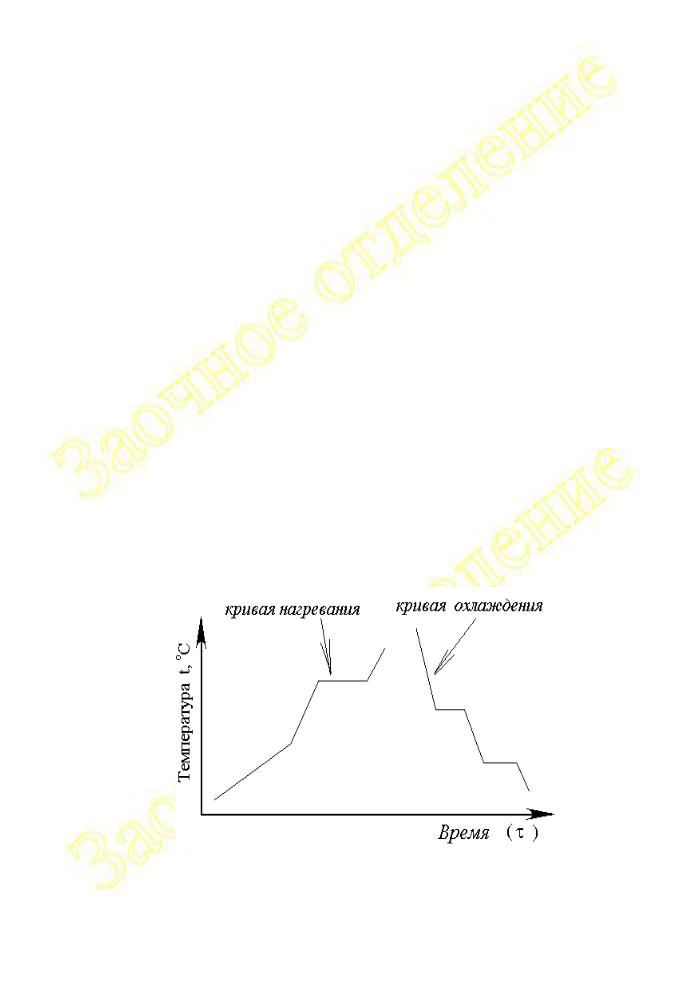
Графические зависимости, отражающие характер изменения температуры системы во времени T = f( ), называются кривыми нагревания или охлаждения
(см. рис.2.1.3).
Рис.2.1.3
130
