
- •Оглавление
- •Основы теории вероятностей
- •Случайные события
- •Вероятность событий
- •Условная вероятность. Независимость событий
- •Перестановки и сочетания
- •Формулы Байеса и полной вероятности
- •Дискретные случайные величины
- •Закон распределения случайной величины. Математическое ожидание
- •Дисперсия случайной величины
- •Биномиальное распределение
- •Плотность и функция распределения. Непрерывные случайные величины
- •Равномерное распределение непрерывной случайной величины
- •Нормальное распределение
- •Математическая статистика Вариационные ряды
- •Графическое представление вариационных рядов
- •Показатели вариации Средние вариационного ряда
- •Оценки разброса
- •Статистическое оценивание параметров Выборочные оценки параметров генеральной совокупности
- •Свойства статистических оценок
- •Точечные и интервальные оценки
- •Проверка статистических гипотез
- •Функция Лапласа(таблица значений)
Вероятность событий
Числовая функция Р, определенная на множестве событий, называется вероятностью, если
1)
для любого события она неотрицательна
(Р(А) 0,
0, А),
А),
2)
для достоверного события равна единице
(Р( )
= 1),
)
= 1),
3)
для попарно несовместных событий
вероятность их суммы равна сумме
вероятностей каждого события (если
Аi*Аj=( ),
то
),
то ).
).
Последнее
утверждение называют аксиомой сложения.
Для двух событий она приет вид: А*В = Р(А
+ В) = Р(А) + Р(В).
Р(А
+ В) = Р(А) + Р(В).
Непосредственно из определения следует, что
Р(
 )
= 0 (так как
)
= 0 (так как );
);Р(
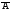 )
= 1 – Р(А) (так как
)
= 1 – Р(А) (так как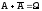 );
);0
 Р(А)
Р(А) 1
(так как
1
(так как );
); ,
т.е. если А
влечет за собой В, то вероятность А
меньше, чем вероятность В (так как
,
т.е. если А
влечет за собой В, то вероятность А
меньше, чем вероятность В (так как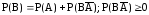 ).
).
Легко
выводится правило сложения вероятностей.
Представим события А + В = А + В и В = В
и В = В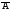 + ВА. События в правых частях равенств
несовместны, поэтому их вероятности
можно сложить по правилу для несовместных
событий (аксиоме сложения):
+ ВА. События в правых частях равенств
несовместны, поэтому их вероятности
можно сложить по правилу для несовместных
событий (аксиоме сложения):
Р(А
+ В) = Р(А) + Р(В );
);
Р(В)
= Р(В )
+ Р(ВА).
)
+ Р(ВА).
Вычтем эти равенства почленно и перенесем Р(В) в правую часть:
Р(А
+ В) = Р(А) + Р(В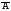 )-Р(В
)-Р(В )-Р(ВА)
+ Р(В);
)-Р(ВА)
+ Р(В);
Р(А + В) = Р(А) + Р(В)-Р(ВА).
Приведенное выше определение вероятности является аксиоматическим.
Если возможные исходы в пространстве элементарных событий равновероятны, используется классическое определение вероятности: вероятность любого элементарного события равна 1/n, где n – общее число элементарных событий. Вероятность случайного события А в соответствии с этим определением равна Р(А) = s/n, где s - число элементарных событий, входящих в соответствующее подмножество.
Это определение подходит, например, для опыта с бросанием монеты, в котором возможные исходы – “герб” или “решка” – равновероятны. Так как их 2, то вероятность каждого – ½. Четыре исхода опыта с двукратным бросанием монеты также равновероятны, и вероятность каждого из них – ¼.
А вот если рассматривать в качестве пространства элементарных событий число выпадений “решки” – 0, 1 или 2, то классическое определение вероятности применить нельзя, так как исходы не являются равновероятными. Тем не менее, вероятность любого из этих исходов можно подсчитать, если рассматривать их как случайные событий в пространстве элементарных событий {ГГ, РГ, ГР, РР}. Например, событие А – “решка выпала 1 раз” - включает в себя два элементарных события: Р(А) = Р{РГ, ГР} = 2/4 = 1/2.
Вероятность события В - “решка выпала хотя бы один раз” - также можно подсчитать с помощью классического определения – так как в него входит 3 элементарных события из четырех, Р(В) = ¾.
Те же результаты можно получить, если воспользоваться правилом сложения вероятностей (все элементарные события несовместны, и их вероятности равны ¼: ¼ + ¼ = ½; ¼ + ¼ + ¼ = ¾).
Вероятность
события
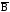 ,
что “решка” не выпадет, равна ¼. Отметим,
что Р(
,
что “решка” не выпадет, равна ¼. Отметим,
что Р( )
= 1-Р(В) = 1-¾.
)
= 1-Р(В) = 1-¾.
На практике не всегда есть возможность судить о том, равновероятны элементарные исходы или нет. В самом деле, предположим, что нам неизвестен тот факт, что выпадение “герба” или “решки” равновероятно. В этом случае следует провести достаточно большое число опытов, например, 1000, и подсчитать число выпадений “решки” (или “герба”). Оно должно оказаться приблизительно равным 500, т.е. половине числа опытов, из чего и будет сделан вывод о равновероятности исходов. Отметим, что если при этом монета имеет какой-то дефект (например, одна ее сторона намагничена), из-за которого исходы действительно не будут равновероятными, в ходе испытаний это выяснится, и ложный вывод о возможности использования классического определения не будет сделан.
Другой пример эмпирического (опытного) определения вероятности – тестирование изделий на наличие брака. Взяв некоторое достаточно большое число изделий (например, 2000), проверим каждое из них. Пусть брак обнаружился в 346 изделиях. Из этого можно сделать вывод, что вероятность наличия брака равна 346/2000 = 0,173. Соответственно, вероятность отсутствия брака равна 1-0,173 = 0,827.
Итак, эмпирически вероятность можно определить, как относительную частоту появления определенного результата при достаточно продолжительном эксперименте, т.е. m/n, где n – достаточно большое общее число отдельных экспериментов, а m – число экспериментов, в которых имел место данный результат.
Иногда эмпирическое определение вероятности еще называют статистическим.
Кроме того, на практике часто встречаются случаи, когда нет ни теоретических данных, ни возможности провести эксперимент. В этом случае для определения вероятности используют экспертную оценку, т.е. ее субъективно оценивает опытный исследователь.
Например, прогноз менеджера по маркетингу: вероятность продажи 1000 единиц товара в первый месяц после его появления на рынке равна 0,4.
Другой пример оценки вероятности специалистом - метеопрогноз: Р(дождь) = 0,4; Р(ветер) = 0,7; Р(дождь и ветер) = Р(дождь*ветер) = 0,2. На этом же примере проиллюстрируем правило сложения вероятностей для событий, не являющихся несовместными. Подсчитаем вероятность того, что будет дождь или ветер: Р(дождь + ветер) = Р(дождь) + Р(ветер)-Р(дождь*ветер) = 0,4 + 0,7-0,2 = 0,9.
Если число исходов является бесконечным, имеет смысл использовать геометрическоеопределение вероятности. В соответствии с этим определением находят вероятность попадания точки в некоторую область. Геометрически вероятность события определяют как отношение меры области, которая соответствует тому, что событие произошло, к мере всей области.
Например, пусть покупатель может зайти в магазин в любой момент времени с 12.00 до 14.00. В 13.00 в магазине могут начать проводить дегустацию товара, которая будет продолжаться полчаса. Найдем вероятность того, что покупатель попадет на эту дегустацию. В качестве всей области рассмотрим отрезок числовой оси от нуля до двух (это те два часа, в течение которых может зайти покупатель). Его мера – длина – равна двум. Та область, которая соответствует дегустации, представляет собой часть этого отрезка длиной 0,5. Таким образом, искомая вероятность равна 0,5/2 = 0,25.
Рассмотрим более сложный пример. Пусть двое покупателей независимо друг от друга собираются прийти в магазин в произвольное время с 12.00 до 14.00. Каждый планирует пробыть там полчаса. Найдем вероятность того, что в магазине одновременно окажутся оба этих покупателя. Для этого обозначим х1– время прихода первого покупателя, а х2– второго. На рисунке 11 квадрат со стороной, равной двум, соответствует всей рассматриваемой области (его мера – площадь – равна 4). Покупатели окажутся в магазине одновременно, если между моментами их прихода пройдет не более получаса, т.е. |х1- х2| ≤ 0,5. Это неравенство можно записать в виде х1- 0,5 ≤ х2≤ х1+ 0,5. На графике область пересечения этих полуплоскостей заштрихована.

![]()
Ее площадь можно вычислить по формуле 4 - 1,5*1,5 = 4 – 2,25 = 1,75. Тогда искомая вероятность равна 1,75/4 = 0,4375.
