Точечные и интервальные оценки

Если оценка параметра представляет собой одно число, такую оценку называют точечной(это точка на числовой оси). Рассмотренные выше оценки являются точечными.

Если при оценивании мы находим интервал значений, в который истинное значение попадает с некоторой вероятностью, то такая оценка будет интервальной. Соответствующий интервал называютдоверительным интервалом, а вероятность –доверительной вероятностью(илинадежностью).

Например, пусть x– средний балл студента.

Пример точечной оценки: = 4,5.

Пример интервальной оценки: 4,2 ≤ ≤ 4,8 (или, что то же самое,= 4,5 ± 0,3) с вероятностью 0,93. Другой пример интервальной оценки: 4,1 ≤≤ 4,9 с вероятностью 0,95 (т.е.= 4,5 ± 0,4).

Следует обратить внимание, что чем больше берется доверительная вероятность, тем шире оказывается доверительный интервал. Собственно, в приведенном примере, даже не зная значение средней, можно точно сказать (с вероятностью 1), что 2 ≤ 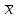≤ 5, так как других значений оценка в этой шкале принять вообще не может. Однако такая информация очевидно бесполезна для исследователя. Чем меньше берется доверительный интервал, тем больше вероятность ошибки, т.е. того, что мы в него не попадем (а доверительная вероятность, соответственно, меньше). Т.е. более точные оценки даются с меньшей вероятностью.

Итак, если границы доверительного интервала для значений некоторого параметра А определяются формулой А ± при доверительной вероятности, то чем больше, тем больше. Для определенияиспользуются формулы, вид которых зависит от того, какой параметр оценивается, каким методом, и выборка какого типа при этом используется. Кроме того, при расчетепо этим формулам используется информация об объемах выборки и генеральной совокупности и о значении. Необходимые формулы можно найти в учебниках и справочниках по статистике.

Проверка статистических гипотез

Статистическая гипотеза– это любое предположение о виде или о значениях параметров вероятностного распределения.

При проверке статистических гипотез ту гипотезу, которую проверяют, принято называть нулевой гипотезойи обозначатьH_о. Одновременно рассматриваютальтернативную(конкурирующую)гипотезуН₁. ГипотезыH_ои Н₁должны быть противоположны друг другу.

Принцип проверки статистических гипотез заключается в следующем. На основе выборки данных рассчитывают некий показатель , который называют статистикой критерия. Этот показатель является случайной величиной (поскольку он рассчитывается по выборке), но его выбирают таким образом, что его вероятностное распределение известно (возможно, приближенно). Кроме того, значениедолжно быть связано с тем, выполняется или нет проверяемая гипотеза. Все возможные значенияразбивают на две непересекающиеся области –область принятия гипотезыикритическую область(в которой гипотеза отклоняется). Например, выбирают критическое значение статистики критерия_кртакое, что если гипотеза верна, то вероятность α превысить это значение α = Р(>_кр) очень мала (α = Р(>_кр)). Тогда при≤_кр гипотеза принимается, а при всех остальных значенияхотклоняетсяH_о.

Правило проверки статистической гипотезы называют статистическим критерием.

Однако, с вероятностью α может быть все же допущена ошибка (т.е. гипотеза H_обудет отвергнута, хотя на самом деле она верна). Это может произойти потому, что значение статистики попало в критическую область случайно. Такую ошибку называютошибкой первого рода, а соответствующую вероятность называютуровнем значимости критерия. Она должна быть небольшой.

Кроме того, может быть допущена также ошибка второго рода : она заключается в том, что гипотезаH_опринимается, хотя на самом деле она является неверной (а верна альтернативная гипотезаH₁). Отметим, что при проверке одной и той же гипотезы по выборке одного и того же объема невозможно одновременно уменьшить вероятность ошибок первого и второго рода. Это связано с тем, что с ростом критической области одновременно растут и α, и. Ведь чем больше критическая область, тем больше вероятность отклонить гипотезу и меньше вероятность ее принять (соответственно, больше вероятность отклонить верную или принять неверную). Вероятность НЕ допустить ошибку второго рода называетсямощностью критерия(она равна 1 –).

Одновременно увеличить мощность критерия и уменьшить уровень значимости можно только за счет увеличения объема выборки, потому что только при этом условии выборочные значения показателей будут более точно отражать истинные характеристики распределения, а вероятность случайных отклонений уменьшится.

Например, на склад поступила партия изделий. Из нее отбирают часть изделий для проверки на брак. По результатам проверки будет принята или отвергнута нулевая гипотеза, которая состоит в следующем: доля бракованных изделий в партии невелика, и партию можно принять. Предположим вначале, что в выбранных изделиях доля бракованных была велика, и по результатам выборочного контроля всю партию забраковали. Однако, есть вероятность, что проверяющему случайно попались именно плохие изделия, и на самом деле партию надо было принять, потому что остальные изделия не содержат брака. В этом случае была допущена ошибка первого рода, т.е. отклонили верную нулевую гипотезу (отвергли хорошие изделия). Теперь предположим, что в выбранных изделиях доля бракованных была невелика, и по результатам выборочного контроля партию приняли. Однако, есть вероятность, что проверяющему случайно попались именно хорошие изделия, и на самом деле партию надо было забраковать. В этом случае была допущена ошибка второго рода, т.е. принята неверная нулевая гипотеза. Из приведенных примеров видно, что чем больше изделий будет выбрано для проверки, тем меньше риск совершить и ту, и другую ошибку. При равном объеме выборки чем строже критерии проверки (больше критическая область), тем больше вероятность допустить ошибку первого рода и меньше – второго (и наоборот).

В юриспуденции под нулевой гипотезой обычно имеется в виду гипотеза о том, что подсудимый невиновен. Соответственно, ошибка первого рода – это обвинение невиновного, а ошибка второго рода – это оправдание виновного. Задание низкого уровня значимости означает, что вероятность ошибки первого рода должна быть маленькой, т.е. риск принять неверное, «обвинить невиновного» должен быть маленьким.

В зависимости от вида критической области все статистические критерии принято делить на три основных класса. Рассмотрим их на примере, в котором статистика имеет стандартное нормальное распределение (т.е.=N(0; 1)) и задан пятипроцентный уровень значимости (α = 0,05):

1) правосторонняя критическая областьзадается неравенством

 > _кр

Если α = 0,05, то площадь под графиком плотности стандартного нормального распределения справа от прямой х = _крдолжна составлять 0,05. Вся площадь под этим графиком справа от вертикальной оси составляет 0,5. Чтобы найти значение_кр, воспользуемся функцией Лапласа, которая должна здесь принять значение 0,5 – 0,05 = 0,45. Такое значение соответствует_кр= 1,64.

На рисунке 20 площадь заштрихованной фигуры составляет 0,05, т.е. 5% от единицы (от общей площади графика под функцией плотности вероятности). Это означает, что Р(>_кр) = α = 0,05. С такой вероятностью проверяемая гипотеза будет все-таки отвергнута, даже если она на самом деле верна. Если фактическое значение статистики критерия≤_кр, гипотеза принимается.

2) левосторонняя критическая областьзадается неравенством

 < _кр

Такое значение соответствует _кр= -1,64. На рисунке 21 площадь заштрихованной фигуры также составляет 0,05, т.е. Р(<_кр) = α = 0,05. Если фактическое значение статистики критерия≥_кр, гипотеза принимается.

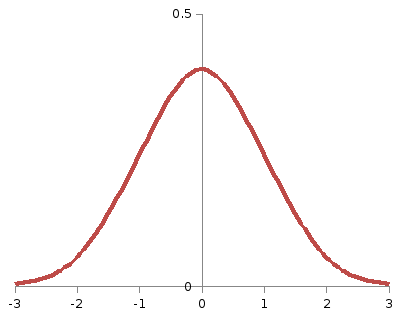
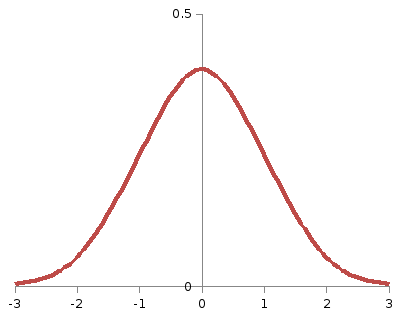
3) двусторонняя критическая областьзадается неравенствами

Поскольку площадь под графиком плотности распределения в критической области должна составлять 0,05, площадь каждого из двух заштрихованных участков на рисунке 22 должна составлять 0,025 (т.е. α/2). Тогда функция Лапласа при х = _кр2должна принять значение 0,5 – 0,025 = 0,475. Такое значение соответствует_кр2= 1,96. Соответственно,_кр1= -1,96.

Итак, при использовании двустороннего критерия Р(<_кр1) = = Р(>_кр2) = α/2. Если_кр1≤≤_кр2, гипотеза принимается.

Рассмотрим следующий пример. Машина для расфасовки специй при поставке была отрегулирована так, чтобы средняя масса специй в пакетике в пробной партии из 50 штук составляла ₀= 90 (г) при СКО_х= 10 (г). Из расфасованной через месяц партии было отобрано 60 пакетиков, и средняя масса специй в пакетике составила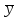₀= 86 (г) при СКО_y= 8,5 (г). Необходимо выяснить, является ли это случайным совпадением, или регулировка машины нарушена.

Сформулируем нулевую гипотезу: регулировка не нарушена. Это означает, что на самом деле средние величины при поставке и в настоящий момент равны, т.е. М(-) = М() – М() = 0. Будем считать, что случайная величина-имеет нормальное распределение с математическим ожиданием 0.

Найдем СКО этой случайной величины.

Какова дисперсия случайной величины ?D() =D((x_i)/n)) = = (D(x_i))/n²= (D(x_i))/n²=²_х*n/n²=²_х/n, гдеn= 50, т.е.D() = 100/50 = 2.

Аналогично D(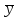) =²_y/n, гдеn= 60, т.е.D(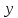) = 8,5²/60 = 72,25/601,2.

Тогда D(-) =D() +D() = 3,2, а СКО1,79.

Итак, (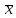-) =N(0; 1,79).

Тогда статистика = (-)/1,79 будет иметь стандартное нормальное распределение, т.е.=N(0, 1). Взяв в качестве оценок генеральных средних выборочные оценки₀и₀, рассчитаем фактическое значение статистики критерия:= ()/1,792,23.

Зададимся уровнем значимости 5%. Построим двустороннюю критическую область: если фактический критерий попадает в нее, то это означает, что разница между средними слишком существенно отличается от нуля в ту или другую сторону; и тогда гипотезу о равенстве средних надо отвергнуть. По таблице функции Лапласа найдем границы этой области: Ф(_кр2) = 0,5 – 0,05/2 = 0,475, тогда_кр2= 1,96;_кр1= -1,96. Так как 2,23 > 1,96, гипотеза Н₀отвергается, т.е. регулировка машины нарушена. Однако, существует пятипроцентная вероятность, что этот вывод сделан случайно (т.е на самом деле с машиной все в порядке, просто были сделаны неудачные выборки).

Зададимся уровнем значимости 2%. Тогда границы критической области найдем по таблице функции Лапласа для значения этой функции Ф(_кр2) = 0,5 – 0,02/2 = 0,49, тогда тогда_кр2= 2,34;_кр1= -2,34. Так как 2,23 > 2,34, на двухпроцентном уровне значимости можно принять нулевую гипотезу. Т.е. считать, что регулировка машины не нарушена.